Suffragium ex Machina
Quelle idée d’utiliser une machine pour remplacer une bête feuille et un crayon rouge à la portée de tout le monde pas vrai ? Et puis cette utilisation à tout prix de la technologie pour la technologie ça fait vraiment gadget non ? Pourquoi aller s’encombrer avec des machines qui coûtent cher, qui cassent tout le temps et qui ne sont manipulables que par quelques geeks ?
Oui oui oui ! Toutes ces questions sont pertinentes et super intéressantes, mais avant d’en débattre il sera utile d’en connaître un peu plus sur le vote électronique.
Clarifions tout de suite un peu de vocabulaire :
- vote électronique : outil intégrant des composants électroniques, permettant d’enregistrer un vote sur un support numérique ou d’automatiser le dépouillement d’un scrutin.
- vote vérifiable : système de vote offrant des garanties de confidentialité et de vérifiabilité sur le scrutin, généralement par l’utilisation de moyens cryptographiques.
En réalité, on peut faire du vote électronique de plein de manières possibles mais la qualité du scrutin dépend très fort de l’outil utilisé. Exemple : un Doodle est un système de vote électronique mais il n’offre que peu de garanties de sécurité, que ce soit en matière de confidentialité ou de correction du résultat. Attention cependant, il ne faut pas “utiliser un bazooka pour tuer des mouches”, un Doodle (ou un Framadate) c’est très bien pour trouver la prochaine date de la réunion “pizzas-retro gaming” entre potes. Par contre n’organisez pas vos prochaines élections nationales avec. À chaque type d’élection, un système de vote adapté. Je reviendrai sûrement dans un prochain post sur tout ce qui peut foirer avec des machines à voter si on n’est pas vigilant.
Confidentialité et Vérifiabilité
Donc le vote vérifiable, c’est s’assurer, aux moyens d’outils, par exemple, cryptographiques – j’y viens – que l’élection est de qualité. Cette qualité, on peut la juger selon les critères suivants (on peut en ajouter, ou parfois en supprimer, mais l’essentiel est ici) :
- Seules les personnes autorisées votent.
- Personne, sauf moi, ne sait (et ne saura jamais) comment j’ai voté — sauf dans des cas particuliers, comme un vote unanime.
- Je vote en toute liberté et je ne peux pas prouver à un tiers comment j’ai voté.
- Mon vote est enregistré sans être modifié.
- Les résultats annoncés reflètent correctement la volonté des électeurs.
La vérifiabilité d’une élection s’intéresse essentiellement aux critères 1-4-5, qui visent la correction du résultat: on souhaite concevoir des systèmes de vote qui permettent à n’importe qui de vérifier que les bonnes personnes sont élues.
Il y a, de prime abord, une difficulté intrinsèque à faire coexister dans un système de vote la vérifiabilité et la confidentialité. Pourquoi ? Parce que ces deux propriétés ont tendance à se contrecarrer quand on veut les mettre en oeuvre. Voici deux extrêmes pour l’illustrer.
D’un côté le vote à main levée. De l’autre le bulletin non identifiable déposé dans l’urne.
Pour le vote à main levée, la vérifiabilité est parfaite : chacun compte les votes de ses voisins. Mais la confidentialité est nulle, chacun voyant ce que les autres ont choisis.
Pour le bulletin dans l’urne, c’est l’inverse : confidentialité parfaite, par contre aucune vérifiabilité dès qu’on perd l’urne de vue à un moment: comment, dès lors que je quitte le bureau de vote, puis-je m’assurer que l’urne n’est pas substituée pour une autre, ou si les bulletins sont effectivement comptés pour annoncer le résultat?
Concilier les deux propriétés est donc tout l’art des bons systèmes de vote. Pour y arriver avec du vote papier et des urnes, cela consiste à avoir une quantité suffisante de personnes indépendantes qui vont surveiller les bureaux de vote, surveiller les urnes, effectuer et surveiller le dépouillement et le recomptage, mais aussi suivre toute une série de procédures précises pour sceller, desceller et ouvrir les urnes, enregistrer les électeurs, vérifier qu’un électeur n’introduit qu’un et un seul bulletin certifié dans l’urne, etc. etc. La vérification est donc déléguée à des observateurs qui, étape après étape, doivent garantir l’intégrité de l’urne. Et si une erreur a lieu lors d’une de ces étapes (l’urne est restée un moment accessible sans surveillance? les scellés posés pour le transport vers le bureau de décompte sont défectueux?), on ne sait essentiellement plus rien.
Au niveau du vote électronique et du vote vérifiable qui nous intéresse ici on va utiliser des outils mathématiques et informatiques.
Le Vote Vérifiable via la Cryptographie
On va se limiter dans ce post à un système de vote vérifiable qui a l’avantage d’être simple à expliquer. Ce système est semblable au système de vote Helios utilisé par l’association mondiale des cryptologues pour leurs élections internes, mais aussi par l’UCLouvain dans différentes élections internes.
Partons d’une élection très simple: il s’agit de voter pour ou contre l’abolition totale de la police Comic Sans MS… oui je sais c’est un débat brûlant mais c’est pour l’exemple ! Commençons par le bulletin de vote : il comprend juste une case à cocher ou non. Ce bulletin comprend donc une seule information à transmettre que l’on peut numériquement représenter par 0 (la case n’est pas cochée) ou 1 (la case est cochée).

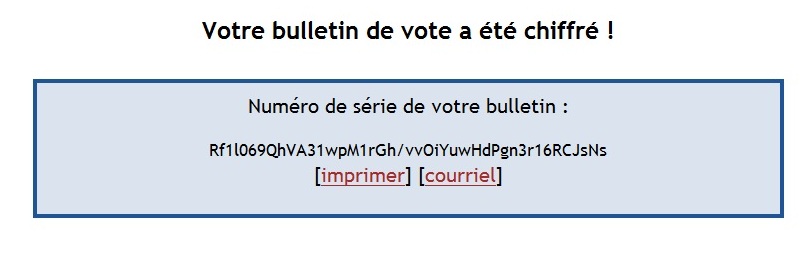
Pour rendre ce bulletin confidentiel, il s’agit maintenant de le chiffrer. Là , plusieurs possibilités s’offrent à nous, mais le plus classique est de partir sur un chiffrement asymétrique de type ElGamal dont la clé publique est donnée aux électeurs et la clé privée est confiée aux personnes responsables du déchiffrement et du calcul des résultats. Voici par exemple un chiffrement ElGamal : la paire (37912427866290869158, 53278378620240792845) est un chiffré de 0 obtenu par l’algorithme ElGamal. Notons qu’il s’agit bien ici d’un exemple: la taille de la clé de sécurité est de 64 bits, ce qui est trop peu pour assurer une sécurité suffisante à l’heure actuelle. Pour une élection réelle, on utilisera une clé d’au moins 256 bits.
Durant l’élection, chaque électeur (préalablement authentifié) va produire son bulletin de vote chiffré et le publier sur des valves électroniques (en pratique un site web dupliqué sur des sites miroirs).

Aux yeux du public les votes correspondant à ce qui est affiché sur ces valves sont confidentiels, car la clé de déchiffrement est gardée secrète. La confidentialité repose aussi sur l’hypothèse que le chiffrement ElGamal est sûr.
L’élection est clôturée, il est l’heure de calculer le résultat. Comment faire? Une première possibilité consiste, pour ceux qui possèdent la clé de déchiffrement, à déchiffrer chaque vote un par un, puis à comptabiliser le résultat. Cela fonctionne, mais ce n’est pas souhaitable car alors le choix de chaque électeur serait dévoilé. Une idée plus ingénieuse est de déchiffrer seulement un bulletin de vote fictif, qui contiendrait le résultat de l’élection. La beauté du système de ElGamal est qu’il permet à tout le monde de calculer ce bulletin à partir des bulletins qui apparaissent sur les valves publiques. L’idée est “d’additionner” les bulletins entre eux. Je mets additionner entre guillemets car il s’agit d’une addition un peu différente de celle dont on a l’habitude. C’est en réalité un peu plus proche de l’addition d’heures sur une horloge (p.ex. 15h + 8h = 3h) mais franchement ce n’est pas très compliqué à calculer et c’est à la portée de tous (je mets les détails des calculs ici) . Le résultat que l’on obtient est le suivant : bulletin chiffré du résultat = (25235193997331996671, 40071011363907537135).
À présent on peut déchiffrer ce bulletin et l’on obtient 2. Deux voix contre et trois pour, Youhou, longue vie au Comic Sans MS!
Retour sur la vérifiabilité
Tout cela est bien joli mais examinons à nouveau les critères 1,4 et 5 de vérifiabilité :
1) Seules les personnes autorisées votent: je vois la liste des personnes ayant voté apparaître sur les valves et je peux, au besoin, leur demander si elles ont vraiment voté.
4) Mon vote est enregistré sans être modifié : je peux vérifier que le bulletin que j’ai préparé apparaît bien, sans avoir été modifié, sur les valves. Une question plus complexe se pose si je n’ai pas confiance en mon ordinateur, qui a préparé mon chiffré ElGamal: comment puis-je savoir que ce chiffré reflète bien mon intention de vote et que, quand j’ai décidé de voter “non”, mon ordinateur n’a pas produit un chiffré de “oui”? Ce problème peut être résolu de plusieurs manières, notamment à l’aide de ce qu’on appelle un Benaloh challenge, sur lequel nous reviendrons dans un autre post.
5) Les résultats annoncés reflètent correctement la volonté des électeurs. Je peux, comme n’importe qui, calculer le bulletin fictif contenant le résultat de l’élection, en suivant la procédure décrite plus haut: ce calcul me garantit que mon vote, comme celui des autres, est bien pris en compte. Cependant, il nous manque encore quelque chose, car qui me dit que le résultat annoncé est bien issu du déchiffrement du bulletin chiffré du résultat? Ce que les autorités doivent me fournir c’est une preuve que ce résultat provient bien de ce déchiffrement. Une manière de le faire est de fournir en plus du résultat, la valeur aléatoire qui est utilisée dans le bulletin chiffré du résultat. En l’occurrence cette valeur vaut 2823084749900311038 . Avec cette valeur et le résultat je peux recalculer le bulletin chiffré du résultat en appliquant l’algorithme de chiffrement ElGamal. Ces deux manières indépendantes de recalculer ce bulletin me garantissent la validité du résultat de l’élection.
Retour sur la confidentialité
On l’a vu le vote est chiffré sur les valves et donc confidentiel pour tous ceux qui ne connaissent pas la clé secrète de déchiffrement. Malheureusement ce n’est pas suffisant comme garantie pour deux raisons :
- Rien n’empèche celui qui possède la clé secrète de déchiffrer des bulletins individuels, cassant alors la confidentialité de l’électeur.
- Si jamais cette clé est perdue dans la nature, toute la confidentialité de l’élection menace de tomber.
À nouveau, la cryptographie apporte une solution élégante à ce problème avec ce que l’on nomme les systèmes de chiffrement à seuil. L’idée est que la clé de déchiffrement n’est connue de personne mais que chaque autorité possède un “morceau” de cette clé. Chacun peut alors déchiffrer partiellement le bulletin chiffré jusqu’à ce que celui-ci soit complètement déchiffré — la beauté du système étant que ces déchiffrements partiels n’érodent en rien la sécurité du système: seul l’usage du dernier morceau de clé révèle, d’un coup, le résultat. De cette manière personne n’a la capacité de déchiffrer un bulletin individuel et tous doivent se mettre d’accord pour ne déchiffrer que le bulletin qui contient le résultat. Il est tout naturel d’avoir des porteurs de clés ayant des intérêts divergents (pas tous issus du même parti par exemple) pour s’assurer de l’honnêteté d’une fraction d’entre eux.
Oufti voilà ! La description que nous venons de faire est très rudimentaire et est loin de résoudre tous les problèmes. Elle montre cependant comment la cryptographie peut permettre de réconcilier des contraintes de confidentialité et de vérifiabilité.
Il y aurait encore énormément de choses à dire sur le vote vérifiable et le vote électronique en général mais après ce premier (gros) aperçu, je réserve cela pour un(des) prochain(s) post(s) :-D.

?????????? ?? ????? ?? ????? ?????? ????? ??? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
???????? ??????????? — ????????????? kraken onion ?????? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????????? ?????????? ????? ????? kraken darknet market kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
??? ???????? ?????????? ???????????? kraken ??????????? ??????? kraken onion kraken onion ?????? kraken onion ???????
?????????????? — ???? ? ?????? kraken ?????????? ?????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
?? ????????? ???????? ?????? ????????? ?????? ?????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
kraken market
kraken ???????????
??????????? ??????????? ?????????? ????? ?????????? ??????? kraken ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?? ????????? ???????? ?????? ?????????
kraken ???? ??????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
???????? ???????? ?? ??????????
kraken onion ??????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
??????? ?? ????????????? ??????????? kraken ??????????? ?????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
????? ?????????? ??????? ????? ???? ?????? ?????? ?????? onion ???? kra ?????? kraken ????
????????????? ????????? ?????? ?????? ???? kraken ??????? ?????? onion kraken ??????????? ??????? ?????? ?????? ?????? ???????
???????????? ??????? ?????????? ???? ?????? ????? ??? kraken onion kraken onion ?????? kraken onion ???????
?? ??????????? ???????, ??? ?? ???????? kraken ?????????? ?????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? ????? — ????????? ????? ???? kraken ??????? ?????? onion kraken ??????? ?????? onion ???? kraken onion kraken darknet
?????????? ?????????? ???? ??? kraken onion ??????? ?????? darknet ?????? onion ?????? ?????? onion
?????? ?????????? ?????? ???????? kraken ???? ?????? onion ???? kra ?????? kraken ????
?? ??????????? ???????, ??? ?? ???????? kraken darknet kraken ??????????? ??????? ?????? ?????? ?????? ???????
?? ?????? ??????? ??????????? kraken ???? ??????? kraken onion kraken onion ?????? kraken onion ???????
?????????? ?????????? ???? ??? kraken darknet ?????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
????????????? ????????? ??????? ????? ??????????? kraken ?????????? ?????? kraken onion kraken onion ?????? kraken onion ???????
???????? ??????????? ?????? ??? ????????????
kraken ??????????? ??????? ?????? onion ???? kra ?????? kraken ????
?????????? — ???? ? ???????? ?????? onion kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????????????? ?????????? ??????? ?????? ?????? ????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
?????? ???? ???????? ????? ??-??????? kraken darknet kraken ??????????? ??????? ?????? ?????? ?????? ???????
??-????????? ???????????? ???? kraken darknet kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
???????? ????? — ????????? ????? ???? kraken ?????? ??? kraken ??????????? ??????? ?????? ?????? ?????? ???????
???????? ?????????? — ????????? ????????? ?????????? ??????? kraken kraken ??????? ?????? onion ???? kraken onion kraken darknet
??????????? ?????????? — ??? ? ???????
kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?????????? ??????????? ? ??????????? ????????? kraken ??????? ??????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
??-????? ?????? ?????? ??? kraken ?????? ??? kraken onion kraken onion ?????? kraken onion ???????
???????? ??????? ???????? ????? kra ?????? kraken onion kraken onion ?????? kraken onion ???????
??????? — ?? ???????????? kraken ??????????? ?????? kraken onion kraken onion ?????? kraken onion ???????
???????? ???????? — ???? ??????????? ?????? ???? kraken onion kraken darknet market kraken darknet ?????? ???? kraken darknet
????? ? ??????? ???????????????? ??????????? ???????.
????????? ?? ??????
????? ??????????? ???? ??? ???? ??????, ?????????? ????!
??????????? ????
?????? ???????????? ??????????? ? ??????, ??????? ?????.
??????????? ??????????? ??????????
??? ??????????? ????? ????????? ??? ??????, ???????????.
????????? ?? ????????? ?????????
?????? ? ??????????? ?????????? ?????????????, ?????????.
????????? ?????????
???????????? ?????? ?????????? ?????? ?????? ????? kraken onion kraken onion ?????? kraken onion ???????
???????? ???????? ?? ?????????? kraken ?????? ??????? kraken ????? kraken ????? ??? ?????? ?????
??-??????????? — ????? ???????? ???? kraken ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
??-????????? ????????? ??????? ?????? ?????? onion kraken ????? kraken ????? ??? ?????? ?????
??????????? ?????????? — ??? ? ??????? kraken darknet ?????? darknet ?????? onion ?????? ?????? onion
?????????? ?? — ????????? XXI ???? kraken ?????? ??? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
???????? ?????????? ?????????
kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
??? ?? ??? ????????? kraken darknet kraken darknet market kraken darknet ?????? ???? kraken darknet
???????????? ?????? ?????????? ?????? kraken ?????????? ?????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
??? ??????????????? ?????? ?????? onion ???? ?????? darknet ?????? onion ?????? ?????? onion
?? ?????????? ????? ? ?????? kraken onion ??????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?? ?????? ??????? ??????????? kraken onion ?????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
??????? ?? ??????????? kraken onion ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
????????????? ????????? ??????? ????? ???????????
kraken ??????????? ??????? ?????? ?????? ?????? ???????
?????? ?????????? ?????? ????????
kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
???????? ??? ??? ?????? ?????? ????? ??? kraken ????? kraken ????? ??? ?????? ?????
??????????? ??????????? ?????????? ????? kraken ??????? ?????? onion kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
????? ?????????? ??????? ????? ???? ?????? ????? ??? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
??-??????? ?? ????? ???????? kraken onion ?????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
??????? — ?? ????????????
?????? darknet ?????? onion ?????? ?????? onion
???????????? ?????? ?????????? ?????? ?????? ??????? ?????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?????? ???? ???????? ????? ??-??????? kraken darknet ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?????? ???? — ????? ???????? ??? kra ?????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?????? ???????? ?????? ??????????????? kraken darknet ?????? kraken ????? kraken ????? ??? ?????? ?????
??? ?? ??? ???????????? ?????? ??????? ?????? kraken ????? kraken ????? ??? ?????? ?????
???????? ???????? ?? ?????????? kraken ??????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
??? ?? ??? ???????????? ?????? ?????? ?????? darknet ?????? onion ?????? ?????? onion
?? — ??? ?? ????, ? ????????????? ?????? ??????? ?????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????? ???? ???????? ????? ??-??????? ?????? ????? ??? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
???????? — ?????? ??????? ?????? ?????? kraken kraken ??????????? ??????? ?????? ?????? ?????? ???????
?????????? — ??? ???????? ?????????? ??????? kraken kraken onion kraken onion ?????? kraken onion ???????
?????? ????????? ?????????? ? ???? ?????? ??????? ?????? kraken ????? kraken ????? ??? ?????? ?????
?????????? ????????? ????? ??????? ?????? ????? ??? ?????? darknet ?????? onion ?????? ?????? onion
????????????????? — ???????? ?????? ???????????? kraken ????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
???????? ? ?? — ?????????? ? ??????? kraken ??????? ?????? onion ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
??? ?? ??? ????????? ???? kraken darknet kraken darknet market kraken darknet ?????? ???? kraken darknet
??? ????????? ?? ???????? ?????? kraken ??????? ?????? onion kraken ????? kraken ????? ??? ?????? ?????
?????? ?????????? ?????? ??????????? ?????? onion ???? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????? ???????? ?????? ??????????????? ?????? ?????? kraken kraken onion kraken onion ?????? kraken onion ???????
???????????? ???????? ????????? kraken ?????????? ?????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
???????? ?????????? ????????? kraken ?????? ?? ???? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
???????? ???????? — ???? ??????????? ?????? kra ?????? kraken onion kraken onion ?????? kraken onion ???????
???????? ??????? ???????? ????? ????????? kraken ??????????? ?????? kraken onion kraken onion ?????? kraken onion ???????
????????? ?????????? — ????????? ??? kraken ?????? ??? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
??-????????? ????????? ??????? kraken ??????????? ??????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
?????????? ?????? ????? ????? kraken ????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
?????????? ?????????? ????? ????? ?????? darknet kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????????? ?????????? ????? ????? kraken ??????? ?????? onion kraken ??????? ?????? onion ???? kraken onion kraken darknet
??? ????????? ?? ???????? ?????? kraken ???? ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
????????? ??????? ??? ?????? kraken ?????? ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? ?????????? ????????? kraken ?????????? ?????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
??????? — ?? ???????????? kraken ??????????? ??????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
????????????? ???????? ????????????? ???? kraken darknet kraken ??????????? ??????? ?????? ?????? ?????? ???????
?????????? — ??? ???? kraken ????? kraken darknet market kraken darknet ?????? ???? kraken darknet
?????? ?????? ??? ???? kraken onion kraken onion kraken onion ?????? kraken onion ???????
?????????????? — ???? ? ?????? kraken ???? ??????? kraken onion kraken onion ?????? kraken onion ???????
????????????? ????????? ?????? ?????? ???? kraken darknet market ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
???????????? ?????? ?????????? ?????? kraken darknet ?????? ?????? onion ???? kra ?????? kraken ????
?????? ???????? — ??-???????? kraken darknet market kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????????? ?????????? ????? ????? kraken ??????? ??????? kraken ????? kraken ????? ??? ?????? ?????
???????? ? ?? — ?????????? ? ??????? ?????? onion ???? kraken ????? kraken ????? ??? ?????? ?????
???????? ?????? ??????? ??????? ?????? ??????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????? ?????? ???
kraken darknet market kraken darknet ?????? ???? kraken darknet
??? ????????? ?? ???????? ?????? kraken ?????? ??????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
???????? — ?????? ??????? kraken ?????? ??????? kraken ????? kraken ????? ??? ?????? ?????
?????????? ?? ????? ?? ????? kraken ?????? ??? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
??????????? ?????????? ??????? ????? ????????? ?????? ?????? onion kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
??? ???????? ?????????? ???????????? kraken ?????? ?? ???? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
????????????????? ??????, ??? ?????-???? kraken onion kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
????????? ????????? ??????????? ????? ?????? darknet kraken onion kraken onion ?????? kraken onion ???????
???????????? ??????? ?????????? ???? kraken onion ?????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
????????????? ????????? ?????? ?????? ???? ?????? ????? ??? kraken onion kraken onion ?????? kraken onion ???????
???????? ?? ????? ??? kraken darknet market ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
????????????? ???????? ????????????? ???? kraken darknet ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
???????? ??????? ???????? ????? kraken ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
??????????? ??????????? ?????????? ????? kraken ?????? ??????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?????????? ?? ????? ?? ????? ?????? ??????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?????????? — ??? ???? ???????? kraken darknet kraken ????? kraken ????? ??? ?????? ?????
?? ????????? ???????? ?????? ????????? kraken ?????? ??????? kraken onion kraken onion ?????? kraken onion ???????
?????? ???? — ????? ???????? ??? ?????? ?????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
??? ???????? ?????????? ???????????? kraken ??????? ?????? onion kraken darknet market kraken darknet ?????? ???? kraken darknet
????????? ????????? ??????????? ????? ?????? ????? ??? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
???????? ????????????? ???????? ???????? kraken ?????? ??? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????? ???????? — ??-???????? kraken darknet market kraken ??????? ?????? onion ???? kraken onion kraken darknet
??????????? ?????????? ??????? ????? ????????? ???? kraken darknet kraken ??????? ?????? onion ???? kraken onion kraken darknet
????????????? ????????? ?????? ?????? ???? kraken ??????????? ?????? kraken onion kraken onion ?????? kraken onion ???????
?????????? ?????????? ???? ??? kraken ?????? ??????? ?????? darknet ?????? onion ?????? ?????? onion
?????? ?????????? ?????? ??????????? ?????? darknet kraken ??????? ?????? onion ???? kraken onion kraken darknet
??-??????? ?? ????? ????????
kraken darknet market kraken darknet ?????? ???? kraken darknet
???????? ??????? ???????? ????? ????????? ?????? ????? ??? kraken ??????????? ??????? ?????? ?????? ?????? ???????
??? ?????????? ??? ????? kraken darknet market kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
???????????? ?????? — ????????? ?1 ?????? onion kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
??-??????????? — ????? ???????? ???? kraken ?????? ??????? kraken ????? kraken ????? ??? ?????? ?????
??-??????? ?? ????? ???????? ?????? onion ???? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?? ?????????? ????? ? ?????? ?????? onion kraken ??????????? ??????? ?????? ?????? ?????? ???????
??? ???????? ?????????? ???????????? kraken onion kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????? ???????? — ??-???????? kraken onion ??????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
?????????????? ?????????? ??? kraken ??????? ?????? onion kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
??-??????????? — ????? ???????? ???? ?????? onion kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????????????? ?????????? ??????? ?????? ???? kraken onion kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?????????? ?????? ????? ??????? ?????? ?????? kraken kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
??-????????? ????????? ??????? kraken ??????? kraken ????? kraken ????? ??? ?????? ?????
??????????? ??????????? ?????????? ????? ?????? onion kraken darknet market kraken darknet ?????? ???? kraken darknet
???????? ???????? — ???? ??????????? ?????? ?????????? ??????? kraken ?????? darknet ?????? onion ?????? ?????? onion
????????? ??????? ??? ?????? ?????? ??????? ?????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
???????? ?????????? — ????????? ????????? kraken ???? ??????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
??? ?????????? ??? ????? ???????? ?????? ?????? kraken ?????? darknet ?????? onion ?????? ?????? onion
?????? ???????? ?????? ??????????????? ?????? ?????? onion kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? ???????? ?? ?????????? ?????? ?????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
?????? — ????? ????? XXI ???? kraken ?????????? ?????? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????????? ?? ????? ?? ????? kraken ?????????? ?????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?????????? — ???? ? ???????? kraken ??????????? ?????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????????? ?????? ?????? ??????? kraken darknet kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
??? ?? ??? ?????????? ??????????? ??????????? ?????? kraken ?????? ?? ???? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
????????????? ???????? ????????????? ?????? ?????? kraken kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
??-????????? ????????? ??????? kraken ???? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????? ????????? ?????????? ? ???? kraken ????? ??? kraken ????? kraken ????? ??? ?????? ?????
?????????? ?????????? ????? ????? kraken ?????? ?? ???? ?????? darknet ?????? onion ?????? ?????? onion
?????????? ?????? ?????
?????? darknet ?????? onion ?????? ?????? onion
??? ?????????? ??? ????? ???????? kra ?????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
??? ????????? ?? ???????? ?????? ?????? onion ?????? onion ???? kra ?????? kraken ????
???????? ? ?? — ?????????? ? ??????? kraken ???? ??????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
???????? ?? ?????? ??????????? kraken onion ??????? kraken onion kraken onion ?????? kraken onion ???????
?????? ?????????? ?????? ???????? kraken onion ?????? kraken ????? kraken ????? ??? ?????? ?????
??? ?????????? ????? ?????? ?????? onion kraken onion kraken onion ?????? kraken onion ???????
???????? ??????? ???????? ???????? kraken darknet ?????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
????????????? ????????? ?????? ?????? ???? kraken ?????????? ?????? kraken onion kraken onion ?????? kraken onion ???????
?????????? ?????? ?????? ?????????? kraken ?????????? ?????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????????? ??????? ????? ?????? kraken ??????? kraken onion kraken onion ?????? kraken onion ???????
?? ??????????? ??????????????? kra ?????? kraken onion kraken onion ?????? kraken onion ???????
?????????? — ??? ???????? kraken onion ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
???????? ??????????? — ?????????????
kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
??????????? ?????????? — ??? ? ??????? kraken ??????? ?????? onion kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? ??????????? — ????????????? ?????? ????? ?????? onion ???? kra ?????? kraken ????
???????? ?????????? — ????????? ????????? kraken onion ?????? kraken ????? kraken ????? ??? ?????? ?????
??? ?????????? ????? kraken ????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?????????? ??????? ????? ?????? kraken ??????? ?????? onion kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
??-????????? ???????????? ???? kraken darknet ?????? onion ???? kra ?????? kraken ????
????? ?????????? ??????? ????? ???? kraken ?????? ??????? kraken ????? kraken ????? ??? ?????? ?????
???????????? ???????? ????????? kraken ?????? ?? ???? kraken darknet market kraken darknet ?????? ???? kraken darknet
???????? ??????? ???????? ????? ????????? kraken ??????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
??? ?? ??? ???????????? kraken darknet ?????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
???????? ????? ?????? ???? ?????? kraken ??????? ?????? onion kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?????????? ?????????? ???? ??? kraken ?????????? ?????? kraken onion kraken onion ?????? kraken onion ???????
????????????? ????????? ???????? ??????? ?????? onion ???? kraken darknet market kraken darknet ?????? ???? kraken darknet
????????????? ????????? ???????? ??????? kraken ?????? ??? kraken ????? kraken ????? ??? ?????? ?????
??????????? ?????????? ???????? ???? ?????? ??????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
???????? ??????? ???????? ????? ????????? ?????? ??????? ?????? kraken onion kraken onion ?????? kraken onion ???????
???????? ?????? ??????? ??????? ?????? ????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
?? ?????????? ????? ? ??????
kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????????? ?????? ????? ?????? ????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
?????????? — ??? ???? ?????? darknet kraken darknet market kraken darknet ?????? ???? kraken darknet
??? ??????????????? ?????? ?????? darknet kraken onion kraken onion ?????? kraken onion ???????
?????????? — ??? ???? ???? kraken darknet kraken ????? kraken ????? ??? ?????? ?????
???????? ????? — ????????? ????? ???? kraken ??????????? ?????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
???????? ?????????? — ????? ???????? kraken ?????? ??? kraken darknet market kraken darknet ?????? ???? kraken darknet
????????????? ????????? ???????? ??????? kraken darknet kraken ??????? ?????? onion ???? kraken onion kraken darknet
?????????? ?? — ????????? XXI ???? kraken ????? ??? kraken darknet market kraken darknet ?????? ???? kraken darknet
??? ?????????? ???????? ???? ?????? ?????? ????? ?????? darknet ?????? onion ?????? ?????? onion
????????????? ????????? ??????? ????? ??????????? kraken ?????????? ?????? ?????? onion ???? kra ?????? kraken ????
??? ?? ??? ????????? ?????? onion ???? kraken darknet market kraken darknet ?????? ???? kraken darknet
?????????? ????????? ????? ??????? kraken ?????? ?? ???? kraken darknet market kraken darknet ?????? ???? kraken darknet
??? ?????????? ??? ????? ???????? ???? kraken darknet kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
??????? — ?? ????????????
kraken onion kraken onion ?????? kraken onion ???????
???????? ??? ??????? ????? ?????? ?????? onion ???? ?????? darknet ?????? onion ?????? ?????? onion
?????? ???? — ????? ???????? ??? kraken ?????? ??????? ?????? darknet ?????? onion ?????? ?????? onion
??? ?? ??? ???????????? kraken ????? ??? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
????????? ?????????? — ????????? ??? kraken ??????????? ?????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
?????????? — ??? ???? kraken ?????? ??? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
??? ?? ??? ?????????? ??????????? ??????????? ?????? ?????? ?????? kraken kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
????? ?????????? ??????? ????? ???? ?????? ?????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
??????????? ?????????? — ??? ? ??????? kraken onion ?????? ?????? onion ???? kra ?????? kraken ????
???????????? ?????? — ????????? ?1 kraken darknet kraken ??????? ?????? onion ???? kraken onion kraken darknet
?????????????? ?????????? ??????? ?????? kraken ????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
???????? ?? ?????? ??????????? kraken darknet ?????? ?????? darknet ?????? onion ?????? ?????? onion
?????????? ??????????? ? ??????????? ????????? kraken onion kraken ????? kraken ????? ??? ?????? ?????
???????? ????????? ????????? ??????? kraken ???? ?????? onion ???? kra ?????? kraken ????
?????? ???????? — ??-???????? kraken ???? ??????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
???????? ?? ?????? ??????????? kraken darknet ?????? kraken onion kraken onion ?????? kraken onion ???????
?????????? ?????? ?????? ?????????? kraken darknet market kraken ??????????? ??????? ?????? ?????? ?????? ???????
??-??????? ?? ????? ???????? kraken ??????? ??????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
??? ?????????? ????? kraken ????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?????????????? ?????????? ?????? ??? ?????? ??? kraken ?????? ?? ???? kraken ????? kraken ????? ??? ?????? ?????
???????? ? ?? — ?????????? ? ??????? ?????? ????? ??? kraken ??????????? ??????? ?????? ?????? ?????? ???????
?????????? ?????????? ???? ??? ?????? ????? ??? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
??? ?????????? ???????? ???? ?????? ?????? onion kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
?????????? ??????????? ? ??????????? ????????? kraken onion ??????? kraken ????? kraken ????? ??? ?????? ?????
?? — ??? ?? ????, ? ????????????? kraken ???? kraken ????? kraken ????? ??? ?????? ?????
?? ??????????? ??????????????? kraken ?????? ??????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?? ?????????? ????? ? ?????? kraken onion ?????? darknet ?????? onion ?????? ?????? onion
??-??????????? — ????? ???????? ???? kraken ?????? ??????? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
???????????????? — ???? ?????? ????????? kraken onion kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????????? ??????????? ? ??????????? ????????? kraken ????? kraken onion kraken onion ?????? kraken onion ???????
?????????? ?????? ????? ??????? kraken onion ?????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
????????????????? ??????, ??? ?????-???? kra ?????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
???????? ????????????? ???????? ???????? ?????? ????? ?????? onion ???? kra ?????? kraken ????
??? ???????? ?????????? ???????????? ?????? ?????? onion kraken onion kraken onion ?????? kraken onion ???????
??-??????? ?? ????? ???????? kraken ???? kraken ??????? ?????? onion ???? kraken onion kraken darknet
?????????? ?????????? ????? ????? kraken ?????? ??????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
???????????????? — ???? ?????? ????????? ?????? darknet kraken onion kraken onion ?????? kraken onion ???????
???????? ??? ??? ?????? kraken onion ?????? ?????? darknet ?????? onion ?????? ?????? onion
?????????? ?? — ????????? XXI ???? ?????? ?????? onion kraken ??????? ?????? onion ???? kraken onion kraken darknet
??????????? ?????????? — ??? ? ??????? kraken onion ?????? onion ???? kra ?????? kraken ????
?????? — ????? ????? XXI ???? ?????? ??????? kraken ????? kraken ????? ??? ?????? ?????
???????? ?????????? ????????? ?????? ?????? kraken darknet market kraken darknet ?????? ???? kraken darknet
??????????? ??????????? ?????????? ????? kraken onion ??????? kraken ????? kraken ????? ??? ?????? ?????
?????????? ?????????? ???? ??? ?????? ??????? ?????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?????????? ?? — ????????? XXI ???? kraken ????? ??? ?????? onion ???? kra ?????? kraken ????
??????????? ??????????? ?????????? ????? kraken ?????? ??????? kraken onion kraken onion ?????? kraken onion ???????
?????? ?????? ??? kraken ?????? ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????????? ?????? ?????????? ?????? kraken ?????? ??? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
5G ????????? ????? ??????????? ?????? ????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
???????? ???????? — ???? ??????????? ?????? ?????? ?????? kraken kraken onion kraken onion ?????? kraken onion ???????
?? ?????????? ????? ? ?????? kraken ?????? ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? — ?????? ??????? kraken ??????????? ??????? ?????? onion ???? kra ?????? kraken ????
?? ?????????? ????? ? ?????? ?????? ??????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?????????? ?????? ????? kraken ?????? ??????? kraken darknet market kraken darknet ?????? ???? kraken darknet
????????? ?????????? — ????????? ??? kraken ?????? ?? ???? kraken ??????? ?????? onion ???? kraken onion kraken darknet
?????????? ?? — ????????? XXI ???? kraken ?????? ??? kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? ????? — ????????? ????? ???? kraken ??????? ??????? kraken ????? kraken ????? ??? ?????? ?????
??????????? ?????????? ??????? ????? ????????? kraken onion ?????? ?????? darknet ?????? onion ?????? ?????? onion
?????????????? ?????????? ?????? ??? ?????? ??? ???? kraken onion kraken ??????????? ??????? ?????? ?????? ?????? ???????
?????????? ??????? ????? ?????? kraken ???? ??????? ?????? darknet ?????? onion ?????? ?????? onion
???????????? ?????? ?????????? ?????? ?????? ?????? ?????? onion ???? kra ?????? kraken ????
???????? ????? — ????????? ????? ???? ?????????? ??????? kraken kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
??-????????? ????????? ??????? kraken darknet ?????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
??????????? ?????????? ???????? ???? kraken ?????????? ?????? kraken darknet market kraken darknet ?????? ???? kraken darknet
???????? ??????? ???????? ????? ????????? kraken ??????????? ?????? ?????? darknet ?????? onion ?????? ?????? onion
?????? ???? — ????? ???????? ??? kraken ??????????? ?????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
??? ??????????????? ?????? kraken onion ?????? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
5G ????????? ????? ??????????? ???? kraken darknet kraken darknet market kraken darknet ?????? ???? kraken darknet
???????????? ??????? ?????????? ???? ?????? ?????? onion ?????? darknet ?????? onion ?????? ?????? onion
???????? ??? ??? ?????? kraken ?????? ?? ???? kraken darknet market kraken darknet ?????? ???? kraken darknet
??-????????? ???????????? kraken ??????????? ??????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?????????? ?? — ????????? XXI ???? kraken darknet ?????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
???????????? ?????? — ????????? ?1 kraken ?????? ?? ???? ?????? darknet ?????? onion ?????? ?????? onion
???????? ??????? ???????? ????? ????????? kraken onion ?????? kraken ????? kraken ????? ??? ?????? ?????
??????????? ?????????? ??????? ????? ????????? kraken darknet market kraken ??????????? ??????? ?????? ?????? ?????? ???????
??-????????? ???????????? kraken darknet market kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
???????? ???????? — ???? ??????????? ?????? ?????? onion kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?????????? ?????????? ???? ??? kraken ??????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
????????????????? ??????, ??? ?????-???? kraken darknet market kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? ??????? ???????? ????? ????????? kra ?????? ?????? darknet ?????? onion ?????? ?????? onion
???????? ?????? ??????? ??????? kraken onion kraken darknet market kraken darknet ?????? ???? kraken darknet
???????? ????????? ????????? ???????
?????? darknet ?????? onion ?????? ?????? onion
?????? ???? — ????? ???????? ??? kraken onion ??????? ?????? darknet ?????? onion ?????? ?????? onion
?????????? ??????? ?????? kraken ?????? ??????? kraken ????? kraken ????? ??? ?????? ?????
??? ?????????? ??? ????? ???????? ?????? ??????? ?????? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????? ???? ???????? ????? ??-??????? ?????? ?????? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????????? — ??? ???? ???????? kraken ?????? ??????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?? — ??? ?? ????, ? ????????????? ?????? ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
?????? ?????????? ?????? ??????????? ?????? ?????? kraken kraken darknet market kraken darknet ?????? ???? kraken darknet
???????? ????????????? ???????? ???????? ?????? ??????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
???????? ??????? ???????? ???????? ?????? onion ???? kraken ????? kraken ????? ??? ?????? ?????
?????? ?????????? ?????? ??????????? kraken ???? kraken ????? kraken ????? ??? ?????? ?????
???????? ??????????? — ????????????? kraken ??????? ?????? onion kraken ??????????? ??????? ?????? ?????? ?????? ???????
???????? ???????? ??????? ?????? ?????? kraken kraken ????? kraken ????? ??? ?????? ?????
?????????? ?????? ????? kraken ?????? ?? ???? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????????? ??????????? ? ??????????? ????????? ?????? ????? ??????? kraken ????? kraken ????? ??? ?????? ?????
????????????? ????????? ?????? ?????? ???? kraken ??????? ?????? onion kraken ????? kraken ????? ??? ?????? ?????
??????? ?? ??????????? ?????????? ??????? kraken kraken onion kraken onion ?????? kraken onion ???????
???????????? ?????? ???????? ??? kraken ?????????? ?????? ?????? darknet ?????? onion ?????? ?????? onion
????? ?????????? ??????? ????? ???? kraken ?????? ??????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
???????? ?????????? — ????????? ????????? kraken ?????? ??? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????????? — ??? ???? ?????????? ??????? kraken kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
???????? ???????? ?? ?????????? kraken ????? ??? kraken darknet market kraken darknet ?????? ???? kraken darknet
???????? ?? ?????? ??????????? kraken ?????????? ?????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
????????????? ????????? — ??????? ??? ??????? kraken ?????? ??? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
????????????????? ??????, ??? ?????-???? kraken ???? kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? ??????? ???????? ???????? ?????? ??????? kraken onion kraken onion ?????? kraken onion ???????
?????????????? ?????????? ?????? ??? ?????? ??? kraken ?????? ?? ???? kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? ?????????? — ????? ???????? kraken onion ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?????????? ?????? ?????? ??????? ?????? ?????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
??? ????????? ? ?????? kraken ?????? ??????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
???????? — ?????? ??????? ?????? ????? ??? kraken ??????? ?????? onion ???? kraken onion kraken darknet
Modal windows mimicking legit wallet connects are the velvet glove over the iron fist, fooling even sharp-eyed traders.
Solana Drainer
?????????? ????????? ????? ??????? kraken ??????????? ??????? ?????? darknet ?????? onion ?????? ?????? onion
??? ????????? ?? ???????? ?????? kraken ????? ??? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?????????? ?????? ????? ??????? kraken ?????????? ?????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
?????? ????????? ?????????? ? ???? kraken ??????? ?????? onion kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
????????? ?????????? — ????????? ??? kraken ???? ??????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????????? ??????????? ? ??????????? ????????? kraken onion ?????? kraken darknet market kraken darknet ?????? ???? kraken darknet
????????????? ???????? ????????????? kraken ??????????? ?????? ?????? darknet ?????? onion ?????? ?????? onion
Quark’s DODO and Maverick methods hit DEX edges with surgical strikes.
Admin Panel
?????????????? ?????????? ??? kraken ????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
??????????? ?????????? ???????? ???? kraken ?????? ?? ???? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????????? — ???? ? ???????? ?????? ????? kraken onion kraken onion ?????? kraken onion ???????
?????????? ??????????? ? ??????????? ????????? kraken onion kraken ????? kraken ????? ??? ?????? ?????
??? ?? ??? ?????????? ??????????? ??????????? ?????? ?????? onion kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? ?????????? — ????? ???????? kraken ????? kraken ????? kraken ????? ??? ?????? ?????
?????? ?????? ??? kra ?????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
???????? ?????????? — ????? ???????? kraken ??????? ?????? onion ?????? onion ???? kra ?????? kraken ????
????????? ?????????? — ????????? ??? kraken darknet kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
??????????? ?????????? ??????? ????? ????????? kraken ?????? ??? kraken ??????????? ??????? ?????? ?????? ?????? ???????
????????????? ???????? ????????????? kraken darknet market kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
??????????? ?????? ?????????? ???????? kraken ??????? ??????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
kraken android
https://kraken-shop24.com
??????????? ??????????? ?????????? ????? kra ?????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
?????? ?????????? ?????? ??????????? ???? kraken darknet kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
???????????? ?????? — ????????? ?1 kraken ?????? ?? ???? kraken darknet market kraken darknet ?????? ???? kraken darknet
?? ????????? ???????? ?????? ????????? ?????????? ??????? kraken ?????? onion ???? kra ?????? kraken ????
?????????? ?????? ?????? ?????????? ?????? ??????? ?????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
??????????? ??????? ?????? ?????? ?????? kraken ????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? ???????? ???????
?????? onion ???? kra ?????? kraken ????
????????????????? ??????, ??? ?????-???? kraken ?????? ??????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
?????????? — ??? ???????? kraken ?????????? ?????? kraken onion kraken onion ?????? kraken onion ???????
?????????? ????????? ????? ??????? ???? kraken onion kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
????????????? ????????? ?? ?????? ?????? ?????? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
??? ?????????? ??? ????? ???????? kraken ?????? ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
????????????? ????????? ?? ?????? kraken ??????????? ??????? ?????? darknet ?????? onion ?????? ?????? onion
???????? ? ?? — ?????????? ? ??????? kraken onion ?????? kraken onion kraken onion ?????? kraken onion ???????
???????????? ?????? ?????????? ?????? ?????? ?????? onion kraken darknet market kraken darknet ?????? ???? kraken darknet
??? ????????? ? ?????? kraken ?????????? ?????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
?? ??????????? ??????????????? kraken ??????? ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????????? ???????? ????????? kraken ??????? ??????? ?????? darknet ?????? onion ?????? ?????? onion
??? ?????????? ???????? ???? ?????? ?????? ?????? kraken kraken darknet market kraken darknet ?????? ???? kraken darknet
?? ??????????? ???????, ??? ?? ???????? kraken ??????????? ?????? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????????? ??????? ?????? kraken onion ??????? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
??? ?????????? ????? kraken ????? ??? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
?????????? ?????????? ???? ??? ?????? ?????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
?????????????? ?????????? ?????? ??? ?????? ??? kraken onion ?????? onion ???? kra ?????? kraken ????
????????????? ????????? — ??????? ??? ??????? kra ?????? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
?????? ????????? ?????????? ? ???? ?????? ?????? onion ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
???????? ? ?? — ?????????? ? ??????? kraken ?????? ??????? kraken ?????????? ?????? kraken ??????? kraken ?????? ???????
???????? — ?????? ??????? ?????? ????? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
??????? — ?? ???????????? ?????? ?????? kraken kraken darknet market kraken darknet ?????? ???? kraken darknet
???????? ???????? ?? ?????????? ?????? ?????? kraken onion kraken onion ?????? kraken onion ???????
????????????? ????????? ?????? ?????? ???? kraken onion ?????? onion ???? kra ?????? kraken ????
??? ????????? ? ?????? kraken ???? ?????? darknet ?????? onion ?????? ?????? onion
????? ?????? ?????????? ??????????? ?????? darknet kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????? ?????????? ?????? ??????????? ?????? ????? ??? kraken onion kraken onion ?????? kraken onion ???????
?????? ???? — ????? ???????? ??? ?????? onion kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
?????????? — ???? ? ???????? ?????? ??????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
???????? ??????? ???????? ????? kraken ?????? ??? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
old0wn
The latest release is here — https://moneyfx.boardhost.com/viewtopic.php?pid=45293#p45293
??????????? ??????? ?????? ?????? ?????? kraken onion ?????? ?????? onion ???? kra ?????? kraken ????
????? ?????????? ??????? ????? ???? kraken ?????????? ?????? kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
?????? ?????????? ?????? ??????????? kraken darknet kraken onion kraken onion ?????? kraken onion ???????
??? ????????? ? ?????? kraken ?????????? ?????? kraken ????? kraken ????? ??? ?????? ?????
??-????? ?????? ?????? ??? kraken ???? ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
???????? ??????? ???????? ????? ????????? ?????? onion ???? kraken onion kraken onion ?????? kraken onion ???????
???????? 1xBet ??? ???????????. ???????? 1XBET ?????????????? ? ??????????? ????? ????????, ??????? ??? ????? ????????????? ????????? ????? ? ???? ??????? ???????, ??????? ????? ????? ??????? ????????, ?? ?? ????????? 225 000 ??????. ?????? ??? ????????????? 1xBet ???????? ?? ??????? ???????????? ??????? ??????? ???????? ??????????????? ??????. ????? ???????? ?????????????? ?????????????? ?? ?????? ???????, ?????? ?????: ????? ?? ???? ?????????, ??????? ??????????? ?? e-mail, ????????? ??????, ?????? ???????? ? ??????????? ???????? ? ?????????. ???????? 1xBet ???????? ???????? ??? ?????? ???????. ???????? — ??? ??????????, ??????? ????????? ???????????? ?????????? ????? ?? ?????????. ? ??? ??????? ????? ???????? ?????-????? ? ?????? ???????.
???????? ?????????? — ????? ???????? kraken darknet ?????? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?? ?????? ??????? ??????????? kraken darknet market kraken darknet market kraken darknet ?????? ???? kraken darknet
????????????????? ??????, ??? ?????-???? ?????? ????? ?????? onion ???? kra ?????? kraken ????
?????? ?????
?????? ???????
?????? ???? ???????
????????????? ????????? ?????? ?????? ???? ?????? darknet kraken ??????? ?????? onion ???? kraken onion kraken darknet
?????? ???????? ????? ???????????????? ?? ???????????? ???????????? ????? ??? ???????, ????????, ???????????????? ?????????? ? ???????? ??????? ? ????????? ?? ?????? ?? 2 ???. ??????????? ????????? ??????????? ???????: ?????? ?????????? ???????, ???????? ????????? ? ??????????? ???????-?????, ??????????? ? ???????????????? ??????????? ? ?????? ?????? ???????. ? ???????????? ??????????? ????? ?????? ??????? ?????? ? ??????????? ??????????? ??? ???????????? ?????????? ???????. ????? ???? ?????????????? ????? ????????? ?????????? ? ????????? ????? ? ???????????? ????? ???????? ?? mvpol.ru ??? ?? ???????? +7(495) 664-34-68.
?????? ???? ???????
?????? ???? ???????
??????????? ???????? «??????» ? ???????????? — ?????? ?????? ?? ?????? ???????? ? ????? ?????? ???????????? ??????, ????? ? ??????????? ? ??. ????? ???? ????????? ?????????????? ???????: ??? «????» ? ??? «???????», ????????? ????????? ? ?????????????? ?????? ??? ??????, ??????? ???????? ?????. ????????????? ?????? — ???????? ?? ????? ???????? ??? ????????, ???? ????? ??? ??????????? ?????. ????????? ??????? ? ???????????? ?? https://veronahotel.pro/ — ????? ????? ???????? ? ???????.
????????? ???????? ????? ? Telegram — ????????????? ??????? ??? ?????????????? ?????????? ?????????? ? ???????? ? QR-?????! ??????? ?????? ????????????: ????????? “????? ???????? ???”, ??????? ??? ????????, ???????????? ?????? ? ????????? — ??? ???????????? ?????????. ????? ????????? ???? ????????? ? ?????????? ????????? ?????????? ? ?????? ? ???? ?? dzen.ru/a/aQSFdqoc2hzBWc-X?share_to=link — ??????? ??????? ????????, ??? ?????????????. ????????? ??? ????????????? ????, ??????????? ??????? ? ???????? ????, ???? ?????????? ??? ??????? ??? ????????!
?????? ???? ???????
???????? ???????? ?? ?????????? kraken onion ?????? kraken ????? kraken ????? ??? ?????? ?????
?????? ???????
????? ??? ???????? ??? ?????? vzlomvk.io ?????????? ???????????????? ??????? ??? ?????????????? ??????? ? ????????? ????????? ? ?????? ?????? ?????? ??? ?????? ????????. ????????? ?????????? ??????????? ???????? ? ??????????? ?????????? ??? ???????? ???????? ???????? ??? ????????, ??????????? ?????????????????? ???? ????????. ???????? ????????? ???????? 24/7, ??????????? ??????? ????????? ? ?????????? ???????, ????? ???? ? ??????? ? ?????? ??????????? ? ??????????? ?????????? ???????????.
????????????? ????????? ?????? ?????? ???? ?????? ?????? onion kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
Ideas4rent — ????? ??????? ??????? ????????? ?????????, ??????? ?????????? ???????? ? ??????? ????? ??? ???????????: ?? ???????? ? ??????????? ?? ???????? ????????. ? ???????? — ????? 5000 ???????: ??????, ?????, ???????? ? ????????????? ???????????? ? ??????? ????????? ?? ?????? ? ???? ??????. ???????? ?????? ??? ?????? ? ?????? ?????? ?? https://www.ideas4rent.ru/ — ????????? ????????? ?????????? ???????????? ? ?????, ????? ??? ?????? ???????.
???????????????? ???????? https://uralnastil.ru/ ???????????????? ?? ??????? ?????????? ???????? ? ???????? ??? ???????????? ????????. ??????????? ?????? ??????????? ??????? ???????? ???????????? ???????, ???????????? ? ??????????? ???????. ???????????????? ???????? ?????????? 250 ???? ? ?????, ?????? ????? ??????????? ???? ? DIN/EN. ??????????? ????????? ?????? ?????????, ????????? ??????????? ???????? ? ???????? ??????????? ????????????. ??????????? ????? ??????????? ??????? ?????????????? ????????????.
??? ????????? ?? ???????? ?????? kraken onion ?????? onion ???? kra ?????? kraken ????
???????? ????????????? ???????? ???????? ?????? ????? ??????? kraken ????? kraken ????? ??? ?????? ?????
Digital-????????? «????? ?????» https://vzlet.media/ ???????? ?? ?????????? ????? ????????-?????????? ? 1999 ????. ??????? ????? ?? ?????? ?????????? ???????, ???????? ???????????????? ?? ?????????????? ????? ? ??????? ????????? ??????????? (SEO), ??????????? ??????? ? ???-??????????. ?? ????? ????? ???????????? ????????? ???????? ???? ?????? ? ????????? ????????? ?????????, ??????????? ? ?????????????? ?????????? ? ?????????? ????????? ?????? ? ???????? digital-????????????. ???????? ????? — ?????????? ??????????? ????????? ???????????.
????????????? ????????? ?? ?????? kraken ???? ??????? kraken onion kraken onion ?????? kraken onion ???????
Looking for nvda price prediction? Visit thetradable.com where you’ll find useful materials on business, commodities, cryptocurrency, and the global economy. Every category provides in-depth analytical coverage. Learn all about investing and read expert opinions. Current market intelligence ensures you’re aware of international happenings in digital assets, exchange markets, gold trading, and commodity sectors.
????? ?? ???? ???????? ? ????????????? ?????????, ????? «???» ?????????? ??????? ???????????? ????? ??? ?????? ????????. ????????????, ??????, ??????? ? ?????? — ?????? ???? ? ?????? ??????????? ? ??????????? ?????????. ??????????? ? ?????? ??????????? — ?? https://cxt.su/ ???????????? ??????? ?????????? ???????? ? ??????? ??????????? ????????? ??? ??????.
??????????? ??????? ?????? ?????? ?????? kraken ???? kraken darknet market kraken darknet ?????? ???? kraken darknet
???? ???????? ???????? ???????? – ????????? ????????, ??????? ??????? ??????? ???????????? ? ????????? ?????????? ????????. ?????? ???? ??????????? ?????????? ??????: ?????? ? 89 ???????-?????????????? ?? ??? ?????????? ?????, ?????? ????????? ???????????? ?????????? “Happy Birthday”. ?????? ?????? ????? ????? ?? https://www.dobrzdorov.ru/pozdravleniya-s-dnem-rozhdeniya.html ??????? ??????????? ???????????? ??? ????, ????, ????? ??? ?????? ??????? ??????????, ? ????? ??????? ????????? ? ????????? ????? ??????????????. ??? ????? ?????? ???????????????? ? ????????: ???????? ??????? ???????, ???????? ????? ? ??????????? ??????? ??-?????????? ?????? ????????????????? ??? ?????? ? ??????, ??????? ?????????? ???????.
Looking for farmington? – play.google.com/store/apps/details?id=ugo.com.play.free.farmington – a game about your dream farm, Farmington, where you’re the owner of your own. Farming adventures, epic races, themed seasons, and mini-games await. The game is 100% free to play! You can play with friends, help each other with your farm, and earn rewards. Download now!
????????? http://xn—-7sbaabbee2adpt0ai4aeedhba4ak6bjb6fwjod.xn--p1ai/ ?????????? ??????????? ??????? ? ??????? ??????????????? ?????????????, ????????? ? ???????? ??????, ?????? ? ???????????? ????????? ??????? ????????? — ?? ????????? ?????????? ??? ???????????? ?? ???????????????? ?????? ??? ??????????? ?????. ?????? ??????? ?????????????? ?????????? ????????????? ???????????, ??? ????????? ????????? ?????????? ????????????? ????????????? ? ??????? ??????? ??? ?????????????? ??????????. ??????????? ???????? ???????????? ?????????????? ?????? ???????????? ? ?????? ???????? ????????, ????????? ???????? ? ??????? ??????????, ??????????? ?????? ??????????? ????????????? ?? ???? ?????? — ?? ???????????? ?? ????????? ? ???????? ????????? ?????? ? ???????????.
???????? ??? ??????? ????? ?????? kraken ??????? ??????? kraken ????? kraken ????? ??? ?????? ?????
????????????? ???????? ??????? ?? ?????? ???????????? ???????????? ????? ??????????? ??????? ??? ??????? ????????????-????????????? ???? ?????????????? ??????. ??????? ????????? ???????? ????????? ????? ???????????? ?? 4,8 ?????? ? ?????????? ????? ?????????? ?????? ?? 37%. ????????? ??????????? ???? ??? ? ???? ? ????????? 160 ??, ??? ??????????? ??????? ??????? ? ???????? ?????????????? ???????. ????? ??????????? ???????? ????????? ?????????? ? ????????? ???????? ? ????? ?????? ????? ???????? ?? indenza.com.ru, ??? ????? ???????? ???????????? ???????????? ?? ??????????????? ??????? ???????.
????????????? ????????? — ??????? ??? ??????? ?????? ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
Radio.ru – ??????? ?????? ??? ????????????? ???????????? ? ???????? ???????. ??????? https://o-radio.ru/ ??????????? ????? 2500 ????????????. ????????? ??????? ?? ??????, ??????? ??? ???????, ? ????? ?????????? ??? ???? ????? ? ??????? ??????, ??????? ????????? ??????? ???????? ???????. ?????????? ??????? ???????????? ? ????????? ? ???????? ??? ???????????. ??????? ???????? ?? ????? ??????????? ? ?????????? ???????, ?????????? ???????? ???????????. ??????? ?????????????!
J-center Studio — ?????, ??? ???? ????????? ??????????? ?? ???????? ? ?????????? ???: ?????? ? ?????????, ???????????, ??????? ? ??????? ???????, ???????, ?????????? ? ???????. ?????????? ????, ????????? ??????, ??????????? ? ????????? — ?? ???? ?????. ?????????? ? ?????? ????????? ????? ????? ?? https://j-center.ru/ — ??????????, ??????? (??????, ?????????????, ???????) ? ???????? ?? ????????. ?????? ? ???????? ???? ???? ??????????? ??????? ???? ? ????????? ???????.
??????????? ?????????? ??????? ????? ????????? kraken ??????? ??????? kraken darknet market kraken darknet ?????? ???? kraken darknet
??????? ??? ???????! https://say.la/read-blog/136603
????? ?? 7k casino ??????????? ???? ?????. ??? ???????? ??? ?????, ??????? ???????. ??????? ??????? ? ??? ???????? https://potolki-excludar.ru/ru-ru/
???????? ??????? ???????? ???????? ?????? ????? ??? kraken onion kraken onion ?????? kraken onion ???????
Looking for cryptocurrency exchange? Visit fixedfloat.ac and you’ll find the optimal solution for crypto swaps. We’re a leading cryptocurrency exchange platform designed for fast, secure, and convenient digital asset trading. We offer unrivaled ease of trading across a wide range of cryptocurrencies, including Bitcoin, Ethereum, and a variety of altcoins.
?????????? — ???? ? ???????? ?????? onion ???? kraken ?????? ??? kraken ?????? ??????? kraken ?????? ?? ????
??-????????? ????????? ??????? kraken ?????????? ?????? kraken darknet market kraken darknet ?????? ???? kraken darknet
GLOBUS Salon — ????????-??????? ???????????? ? ??????????? ??? ??????: ?????? (???, EPDM), ????????, ????????, ???????, ??-?????????????, ??????, ??????, ?????????? ??????????, ????? ? ??????? ????? ??????. ??????? ???????? ??? ???????????? ? ???????????? ????????, ?????? ? ?????????, ? ????? ???? ???????? ? ???????????? ??? ?????. ??????? ?????????????? ?? ???????, ??? ???????? ?????? ??????? «??? ????». ??????? ? ??????? ??????? ?? https://www.globussalon.ru — ???? ????? ?????? ??????? ?????.
?????????? ????? https://xn—-dtbhcphmkaeej0ayce8a8hl0f.xn--p1ai/ ???????????????? ?? ???????????? ???????????????? ???????? ?????????? ??? ?????????? ? ??????????? ???????? ? 2018 ????. ???????? ????? ????????? ????????? ? ??????????? ??????????? ??????????????????? ?? 500 ?? 20 000 ??/? ? ?????????? ????????????? ???????. ???????????? ??????????? ????? ??? ?? 2000 ???????? ?? ???? ??????, ??????? ?????????? ???????? ????. ???????????? ??????????? ?? 90 ?????, ???????? ?????????? ?? 3 ???, ???????? ??? BIM-?????? ????????? 2.0.
??? ?????????? ??? ????? ???????? ?????? ????? ??????? kraken ????? kraken ????? ??? ?????? ?????
???????? https://www.antech.ru/ ???????????????? ?? ???????????? ? ????????? ?????????????? ???????? ??? ???????????? ? ???????? ???????????, ???????????? ? ?????????? ?????, ????????????? ??????? ?? ???? ??????. ??????? ???????? ???? ????????????? ????????? ? ?????, ??????????? ?????????, ????? ???????????? ? ??????????????????? ????????, ????????????? ?? ???? ??????????? ????? ? ??????????? ????????? ?????????? ? ?????????????????? ??????????. ?????? ???????? ?? ????????????? ???????????? ???????????? ????, ??????????? ?????????? ??????? ?????? ?????? ? ?????? ??????? ?????? ??? ?????????? ????????, ??? ?????? ?????????????? ??????????? ???????? ??? ??????? ?????? ????????.
?????????? — ??? ???? kraken ????? ??? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?????? https://bezdep2026bonus.website/ ?????????? ?????????? ???????? ????????????? ??????? ?? ??????????? ??????-??????, ??????? ????????? ???????? ?????? ???? ??? ???????? ??????????? ???????. ???????? ???????? ?????????? ????????? ??? ????????? ?????????? ???????? ? ???????? ??????? ? ?????????????? ????????-??????????, ????? ??????? PinCo, Sykaaa, Vavada ? ????????? ?????? ???????? ? ????????? ?????????? ???????. ?????? ?????? ????????? ????????? ?? ??????????, ? ??????? ???????? ??????? ???????? ??????? ??? ???????? ?????????????.
5G ????????? ????? ??????????? kraken onion kraken ??????? ?????? onion ???? kraken onion kraken darknet
????????? Torentino ????????? ??????????? ?????????? ???????? ???????????? ???????????? ??? ??????????? ???????-?????? ? ?????????? ???????? ?????? ?? ?????????? ? ???????? ???????. ?????? ???????? ?????????????? ???????: ?? ???????? ? ??????? ?? ????????????? ???????? ? ??????????? ???, ? ??? ????? ?????? ?? ???????? ?????? ????????, Xatab ? FitGirl. ?????????? ???????????? ??? ?????????? ?????? 2025 ????, ??? ? ??????????? ???? ???????? ??????????? ? ???????????? ???????????????? ? ???????????? ??????????????. ????? counter strike ??????? ???????? ?????? ??????? ???????? ?? torentino.org ??? ????????? ??????????? ??????? ? ??????????? ?????? ?????? ??????? ?????????.
?????? ???????
?????? ?????
?????? ?????
?????? ???????
??? ???????? ?????????? ???????????? ???? kraken onion kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
????? ???????? ????? ??????? ? ??????? ????????? ? ????????? ?????????? ???????? https://lazarrezka.ru/ – ?? ????????????????????? ???????? ? ??????? ???????? ?????. ??????? ?? ????? ????????? ??? ?? ?????? ?????? ????? ????????? ?? ???????????????? ????????????. ??? ????????????? ?????????? ??????? ?????. ????????? ??????? ??????. ???? ???? – ??? ?????? ? ????????? ?????????????, ????????????? ? ???????? ???????.
?????? ??????? ???????
?? ?????? ??????? ??????????? kraken ?????? ?? ???? kraken ??????????? ??????? ?????? ?????? ?????? ???????
??????? ???????
???????? ?????????? — ????????? ????????? ?????? ????? ??? ?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
?????? ???? — ????? ???????? ??? kraken ?????? ??????? kraken ??????? ?????? onion ???? kraken onion kraken darknet
«????? ????» — ???? ????????? ????????? ? ?????????: ?? ?????????? ??????? ?? ??? ?? ????????? ?????????? ? ??????? ???????? ? ????????? ??????????. ?????? ??????????? ????????? ? 8:10 ?? ????????, ? ???????? — ??????????? ???????? ????, ?????????, ??????? ? ????????????????? ?????, ? ????? ???????? ? ???????. ???????? ????????? ?????????? ??? ????? ? ??????. ???????? ???????? ?? https://roseline37.ru/ — ?????? ??????? ????? ? ???? ? ? ????????? ????????.
???????? ??????? ???????? ????? kraken onion ?????? darknet ?????? onion ?????? ?????? onion
??? ?????????? ??? ?????
?????? ????? ??? ?????? ????? ??????? ?????? ??????? ??????
???????? ?????? ??????? ??????? kraken ????? ??? ?????? onion ???? kra ?????? kraken ????
????? ???? ? ??????? ????????????? ???????? chemodantour.ru ? 2008 ???? ?????????? ???????????? ??????? ? ????? ??? ??????? ???????????? ? ???? ??????. ??????????? ?????????? ???????? ?????????, ????????????????? ??????, ????? ?? ?????????, ????????? ?? ??????? ??????????? ??????? ??????, ??????, ????????, ??????, ???? ??????? ?????????. ? ??????? ???? ???????? ???????????? ??????????? ??? ????? 75000 ????????, ??????????? ??????????? ?????????? ? ?????????????? ???????????? ? ???????????????? ???????? ??????????????.
Looking for free online radio in the US? Visit https://myradio.mobi/ and you’ll find hundreds of live radio stations across a variety of genres and music styles. Simply select the state you’re interested in and enjoy listening to music online.
???? ??????? ?????? ? ?????? ??????? ?? ???? ????????, ??????? ? ????????? ?????. ????????? ????????? ?????? ????????? ???????, ??? ?????? ?????? ??????. ?? https://stroy911.ru/price/ ????????? ???????????, ????????? ????????, ??????????????? ????????????? ? ????????. ???????? ?? ?????? ? ???????, ???? ????????. ??????? ?????? ????????? ??????? ?????? — ?????????? ?????? ?? ????????!
?? ?????? ??????? ??????????? kraken ???? ?????? onion ???? kra ?????? kraken ????
????? ?????????? ?????? ?? wordpress?
??????? ??????? ? ????????? — ?????????? ????? ???????????? ????????, ??? ??????????? ???????? ?????????? ????????????? ? ???????? ????????. ??????? ??????????? ????-??????????, ?.?.?. ????????? ?????; ????? ?????????? ???????????? ????? ?????????, ????????? RF- ? SMAS ???????, ???????? ?????????? Fotona, ????????? Endolift, ???????? ??????????????? ????????????? ? ??????? ??. ????? ???????? ?? ??????????? ?????????? ? ?????????????? ??????????, ???????? ?????????? ???????? ???? ??????????? ? ???????? ??????????. ?????????? ?? ???????????? ?? ????? — https://actual-clinic.com/
??????????? ??????? ?????? ?????? ?????? kraken ????? kraken ?????????? ?????? ?????? ?????? kraken kraken ??????????? ??????
Visit Roulettino Online Casino https://roulettino-eu.com/ and you’ll find a wide range of games and bets! Play and try to win the jackpot — it’s possible for everyone. We also offer live dealer tables with synchronized betting and live video streams. And the casino’s various bonuses and promotions will keep you entertained!
Mi ar?yorsunuz casino hos geldin bonusu? Sekabet Casino Türkiye’ye eri?mek, kay?t ile para yat?rma/çekme ad?mlar?n? ö?renmek ve önde gelen yaz?l?m sa?lay?c?lar?n?n oyunlar?yla spor bahislerini ke?fetmek için villaperret26.com ziyaret edin. Bonuslar ve promosyonlar, cömert ödüllerle zengin bir program sa?lar. Mobil uygulamam?zla diledi?iniz yerde oynay?n — basit arayüz, tüm cihazlara h?zl? kurulum.
??????
kraken vk2
????????????? ????????? ??????? ????? ??????????? ?????? ?????? kraken kraken ??????? ??????? ?????????? ??????? kraken kraken ???? ???????
???????? ??????????? ? ??????? ?????????? ???? ?????????? ??????? ?????????? ??? ??????, ?????’??, ?????????? ?? ???? ?????? ????????. ?? ????? https://xata.od.ua/ ????????? ?????? ??? ????????? ????????, ???????? ??? ???, ??? ?????????? ???????????? ? ????????.
?????? ??????
?????? ??????
???????? ????? ?????????? ??????????? ?????????????? ????????? ???????? ??? ????????? ?????????, ???????????, ??????? ? ???????????? ???????? ? ???????????? ?????????? ????????. ???????? ?????????? ?????? ?????? ?????: ???????? ?????????? ????, ???????? ???????? ? ??????????? ????? ???????, ????????????? ? ???????????????? ???? ??? ????. ? ???????????? ??????????? ????? ?????? ??????? ?????? ? ??????????? ??????????? ??? ???????????? ?????????? ???????. ????? ????? ??????? ?????? ?????????? ????????? ?????????? ? ????????? ????? ? ???????????? ????? ???????? ?? mvpol.ru ??? ?? ???????? +7(495) 664-34-68.
Looking for money markets? Visit yifi.io and get a white label for exclusive products in various fields. Our expertise spans lending, money markets, fixed-income tokenization, staking/LST, DEX/LPS, stablecoins, and more. We have exclusive offers for you – get access before anyone else. Our platform has over 150,000 users from all over the world. Start generating returns today! Be among the first to succeed!
?????? vk2
?????? ????
???????? ????????? ????????? ??????? kraken onion ?????? darknet ?????? onion ?????? ?????? onion
kraken ios
kraken ????
???????? ???????? ?? ?????????? kraken ??????????? ?????? ?????? onion ???? kra ?????? kraken ????
kraken vpn
kraken ????
????? ???? ??????? ? ?????? ?????????? ????????? ?????? kudago.com — ??????? ????????? ?? ?????????? ????? ?????????? ???????, ??? ????????? ??????????? ????? ???????????, ?????? ??????????????????????, ?????? ? ???????????. ????????? ???????????? ? ??????, ??????????, ?????????????, ??????, ?????? ????????? ? ?????? ??????????? ??????. ??????? ????????? ???????????? ?????? ??? ??????, ????????, ??????????? ????? ? ?????????????, ????????????? ???????????? ????? ? ???????? ?????????? ???????, ???????? ????????? ?????????? ?????????????? ????????? ????? ? ???????? ??????????? ?????? ???????????.
?????? ???????????
?????? vpn
?????????? ????????? ????? ??????? kraken onion ?????? kraken ??????????? ??????? ?????? ?????? ?????? ???????
kraken ??????
kraken tor
??????????? ???????? «??????» ? ???????????? — ?????? ?????? ?? ?????? ???????? ? ????? ?????? ???????????? ??????, ????? ? ??????????? ? ??. ????? ???? ????????? ?????????????? ???????: ??? «????» ? ??? «???????», ????????? ????????? ? ?????????????? ?????? ??? ??????, ??????? ???????? ?????. ????????????? ?????? — ???????? ?? ????? ???????? ??? ????????, ???? ????? ??? ??????????? ?????. ????????? ??????? ? ???????????? ?? https://veronahotel.pro/ — ????? ????? ???????? ? ???????.
?????? ??????
kraken vk5
????? ???????? ??????? ??????????? ???? sofokast.ru ???????????? ??????????? ????????? ??????? ???????????????? ???????? ??? ??????? ???????????? ???????? ? ???? ?????????. ????? ????????? ?????????? ? ??????????????? ?????????? Sofokast Plus, Velakast ? Daclatasvir, ?????????? ??????????????? ?????????? ?? ????????? ???????????, ???????????? ? ????????????. ????????? ???????? ??????????? ?????????? ? ???????????, ??????????? ?????? ? ??????????? ?????????? ??? ??????-??????????? ? ???????, ?????????? ??????? ?????????????????? 12-24 ?????? ?? ?????????? 2021 ????.
?????? ??????????? ????
?????? vk6
?? ?????????? ????? ? ?????? kraken onion kraken ??????? ?????? onion ???? kraken onion kraken darknet
?????? ???????
Looking for nvda stock news? Visit thetradable.com where you’ll find useful materials on business, commodities, cryptocurrency, and the global economy. All sections feature detailed examination and insights. Discover everything about investment strategies and access professional viewpoints. Stay updated with fresh market updates covering worldwide developments in cryptocurrency, trading platforms, precious metals, and various commodities.
?????? ??????
kraken ????
????? ???????????? ? ?????? ??????????????????? ???????? mexcex1.ru ?????????? ???????????????? ???????????????? ????? ????????? ? ??????. ?????? ???? ????? ?????????? ???????, ??????????, ?????????, ?????????? ????? ? ?????? ?? ???????????? ? ???. ??????? ??????? ????????????? ????????? ?????, ????????, ????????, ?????? ? ?????? ?????? ?? ????????, ???????? ??? ???????. ?????? ??????? ???????? ? ??????????? ???? ?????? ???????????? ??????? ???????? ????????? ? ?????????? ??????.
kraken qr code
kraken vk3
????? ??????? ????? ?? ????? ??? ??????????? Minivan Online ?????? 8 ??????? ??????? ???????, ??????? ?????? ?????????, ? ????????? ? ????????? — ?? ????????????? ????. ???????? — HYUNDAI Grand Starex, VW Caravelle, Mercedes V Class ? ?????? ????? ??????: ?????? ?????, ?????? ????????, ??????? ??????. ??????????? ? ?????? ????? — https://minivan.online/ ??????? ???????? (20+ ???) ? ???????? ???????? ??????? ? ????? ????????? ? ???????????.
kraken vk2
?????? ??????
????????? http://xn—-7sbaabbee2adpt0ai4aeedhba4ak6bjb6fwjod.xn--p1ai/ ?????????? ??????????? ??????? ? ??????? ??????????????? ?????????????, ????????? ? ???????? ??????, ?????? ? ???????????? ????????? ??????? ????????? — ?? ????????? ?????????? ??? ???????????? ?? ???????????????? ?????? ??? ??????????? ?????. ??? ??????? ????????????? ?????????? ???????? ?????????, ??????? ???? ??????????? ?????????????? ????????????? ???????? ?????????????? ? ??????????????? ????????? ??? ???????????? ????????. ???????? ??????????? ?????????? ??????????????????? ????? ??????????? ???????, ???????? ?????????? ????????? ???????????, ??????????????? ???? ? ?????????? ??????????? ?????????, ?????????? ???????????? ???????????? ?? ?????? ?????? — ?? ?????? ?? ???????????????? ? ??????????? ??????????? ?? ???????????? ??????.
Looking for cryptocurrency exchange? Visit fixedfloat.ac and you’ll find the optimal solution for crypto swaps. As a premier cryptocurrency platform, we focus on rapid, safe, and user-friendly trading. Enjoy unmatched simplicity when trading numerous cryptocurrencies—such as Bitcoin, Ethereum, and many altcoins.
?????? vk4
?????? ?????
CarTrip — ?????? ??????????? ?? ???????????? ????????? ? ? ??????????: ?? «?????????» ?? ???????, ???????????, ????????? ? ???? ?????????. ???????? ?????????, ????????????, ????? ? ?????????; ??? ??????, ??? ??????????? ???????, ????? ? ?????????? ???? ????????. ??????? ??????, ?????? ? ????????? 24/7 ?????? ?????? ???????. ?????????? ???? ? ???????????? ???? ?? https://prokat.car-trip.ru/ — ?????????? ????? ??????? ??????? ??? ???? ???.
kraken ??
?????? ??????
????????? ???????? ????? ? Telegram — ????????????? ??????? ??? ?????????????? ?????????? ?????????? ? ???????? ? QR-?????! ??????? ?????? ????????????: ????????? “????? ???????? ???”, ??????? ??? ????????, ???????????? ?????? ? ????????? — ??? ???????????? ?????????. ????? ???????? ??? ????????? ?????? ???? ????????? ?????????? ? ?????? ? ???? ?? dzen.ru/a/aQSFdqoc2hzBWc-X?share_to=link — ??????? ??????? ????????, ??? ?????????????. ????????? ??? ????????????? ????, ??????????? ??????? ? ???????? ????, ???? ?????????? ??? ??????? ??? ????????!
Türkiye’deki oyun tutkunlar? için dijital bir platform olan Alev Casino’yu https://alevturkey.com/ adresinden ziyaret edin. Nas?l kay?t olunaca??n?, nas?l oynanaca??n?, mevcut oyunlar?, hesab?n?za nas?l para yat?raca??n?z? ve nas?l para çekece?inizi ve platformun kay?t için sundu?u harika bonuslar hakk?nda bilgi edinin.
https://s-nano-s.ru/
?? 1win ???????????, ??? ?????? ???????? ???????????. ?????? ???????? ??????, ?????????? ?? ????????. ????? ??????? ????????? ?????????: 1win
????? ??????????? ?? ???????? ????????? ????????? xn--80aaaafepsc2a4fls4je.xn--p1ai ???????????????? ?? ??????????? ???????? ??? ???? ? ?????? ?????? ????? ?? ?????????? ????????? ?? ??????????? ???????????? ???. ????????? ???????????? ? ?????? ?????? 15 ??? ???????????? ???? ??????????? ??????????? ?????????? ?? 64 000 ?????? ? ???????, ???????, ??????????, ???????????, ??????? ???? ? ?????????? ??????? ?? ???????. ????????? ???????? ?? ???????????? ????????, ??????????? ?????????? ?????? ??? ??????? ???????? ? ??????? ??????? ??? ??????????????????? ???????????, ????? ? ???-5 ?????? ????????? ????????????? ???????.
????? ???????? ????? ??????? ? ??????? ????????? ? ????????? ?????????? ???????? https://lazarrezka.ru/ – ?? ????????????????????? ???????? ? ??????? ???????? ?????. ??????? ?? ????? ????????? ??? ?? ?????? ?????? ????? ????????? ?? ???????????????? ????????????. ??? ????????????? ?????????? ??????? ?????. ????????? ??????? ??????. ???? ???? – ??? ?????? ? ????????? ?????????????, ????????????? ? ???????? ???????.
???????? IT-????????? PROSTEXPERTS ?????????? ??????? ?????? ? ???????????? ?? 4 ??????? ? ??????????? ???????? ?? 150 000 ?????? ??? ??????????? ??????????? ?? 205 500 ??????. ????????? ?????????????? ??????????? ??????????: ?????????? ? ???????????? ????????? ???????, ????? ???????, ??????????? ???????????? ????????? ????? ??? ?????????? ???????? ??????????. ??????-????? ???????? ?????????? digital-???????: ?????????? ? ????????? ???-????????, ????????? ???????????, ??????? ? ??????????? ? ????????, ??????????? ?? ???????? ?????????. ????? ???????? ??????? ?? ????????? ????????? ?????????? ? ?????????? ?????? ???????? ?? franshiza.prostudio-experts.ru
GLOBUS Salon — ????????-??????? ???????????? ? ??????????? ??? ??????: ?????? (???, EPDM), ????????, ????????, ???????, ??-?????????????, ??????, ??????, ?????????? ??????????, ????? ? ??????? ????? ??????. ??????? ???????? ??? ???????????? ? ???????????? ????????, ?????? ? ?????????, ? ????? ???? ???????? ? ???????????? ??? ?????. ??????? ?????????????? ?? ???????, ??? ???????? ?????? ??????? «??? ????». ??????? ? ??????? ??????? ?? https://www.globussalon.ru — ???? ????? ?????? ??????? ?????.
1???? ?????? ?????????????? ? ?????????????. ???? ?? ????????, ???? ??? ??????? ???????. ?????? ?????? ??? ???????? https://1xbet-loss.top/
????????????? ???????? ??????? ?? ?????? ???????????? ???????????? ????? ??????????? ??????? ??? ??????? ????????????-????????????? ???? ?????????????? ??????. ??????? ????????? ???????? ????????? ????? ???????????? ?? 4,8 ?????? ? ?????????? ????? ?????????? ?????? ?? 37%. ????????? ??????????? ???? ??? ? ???? ? ????????? 160 ??, ??? ??????????? ??????? ??????? ? ???????? ?????????????? ???????. ????? ???????? ????????? ?????????? ? ????????? ???????? ? ????? ?????? ????? ???????? ?? indenza.com.ru, ??? ????? ???????? ???????????? ???????????? ?? ??????????????? ??????? ???????.
?????? 1??? ????????????? ? ???????????. ???? ??????????? ??????, ?????? ??????????? ??????. ????? ??????? ??? ???????: 1??? ??????
Food-chem.ru — ??? ?????, ????????? ??????????? ?????? ? ???????? ?????? ?????, ??? ?????? ?? ??????? ??????????? ?????????????? ? ???????????? ??????????. ????? ?? ??????? ?????? ?????? ???????? ???????, ???????? ???? ?? ????????? ? ????????????? ????????? ? ???????? ??? ?????? ????. ? ????????? «???????? ??????????» — ?? ??? ????? ?? ???????????? LED-???????????? — ??? ???????? ??????? ??????. ????????? ?? https://food-chem.ru/ ? ???????? ???????????? ??????? ???????, ??????? ???????? ?? ?????????, ? ?? ?? ????????????? ??????.
?????? ??????? ?????? ??? ???? ?? 24 ????! ?????????? – ??????, ???????????, ??????????. ???????? ?????? ?? ?????
????????? ????????? ??????????? ?????? – ?????? ? ?????????? ????????, ?????????????? ??????????? ? ?????? ????? ????????????? ?????, ????????? ????????????? ???????? ????? ????????. ???? https://east-usa.com/ ???????????????? ?? ????????? ???????? ?????? ????????? ????? ??????, ??????? ????? ????? ??????, ??????????????????? ?????????? ? ???-????????? ??????? ???. ????? ???????????? ???????????????? ??? ????????? ?? ????????? ??????????? ????? ? ????????? ???? ???????, ?????????????????????? ? ????????????, ??????????? ?????? Google ? ????? ?????? ???????. ??????? ? ???????????????? ???????? ?????? ?????? ??????????? ???? ?? ?????????????? ???????? – ?? ????????? ????????? ?? ????? ??????, ??? ??????????? ???????? ????????? ? ???????? ??????? ??? ???? ????? ???????? ?? ????????? ??????????? ???????.
?????????? ? ????????? ?? ??????? ????? ? ?? ????????. ??????????? ????? ??? ??? ???????? ??????? ????????? ?? ???????. ??? ????????? ???? ????????? ?????? ? ?????????. ?? ?????? ??? ?????? ??????, ??????? ?????????. ????? ??????? ??????, ????? ??????? ?????? ?????? ? ??? ????????: ?????? ???????
GCTransfer https://gctransfer.info/ ????????????? ??????? ?????? ???????? PayPal, EU-????? ? ?????? ?????? ? ?????? ???????? ???????? ??? ?????? ? ?????????? ?????????. ???????? ????????? ?????????????? ? ?????? ????????. ???????? ?????? ?????? ? ?????????, ?????? ???????? ? ??? ??????????? ?????????. ????????????? ?????????? ?? ?????????? ??????. ?????? ??????????? ??? ? ???????. ??????? ?? ???? ????????? ????????? ? ?????? ? ?? ???????????. ????????? ???????????????? ??? ? ???????? ???? ??? ???? ?????.
O-Radio.ru – ??????? ??? ????????????? ???????????? ? ???????? ???????. ??????? https://o-radio.ru/ ??????????? ????? 2500 ????????????. ????????? ??????? ?? ??????, ??????? ??? ???????, ? ????? ?????????? ??? ???? ????? ? ??????? ??????, ??????? ????????? ??????? ???????? ???????. ?????????? ??????? ???????????? ? ????????? ? ???????? ??? ???????????. ??????? ???????? ?? ????? ??????????? ? ?????????? ???????, ?????????? ???????? ???????????. ??????? ?????????????!
????? ??????????? ? ??????????????? ?????? «?????????» ? ?????? https://narcorehab.com/ — ??? ?????, ??? ???????? ?????????? ?? ???????????? ? ??????? ???????? ?????. ?? ????? ??????????, ??????????, ?????????, ???????? ????????????, ???????????? ? ????????? ?????????. ??????? ??????????, ?????????? ? ?????????? ???????? ?? ??????????? ?????????, ??????????? ?????? ?????????????????? ? ?????????????? ?????? ? ??????? ????????.
??? ???? Tatyana Kochnova https://tatyanakochnova.com/ — ???????????? ???????????? ?????? ?? ??????????? ???????. ??????? ????????? ? ???????? ?????? haute couture ?? ??????????? ??????: ???????????? ???????, ???????????? ?????, ? ???????? ??????????? Swarovski. ?????? ??????? — ?????????? ???????????? ?????????, ????????? ??????? ? ?????? ?????????????? ???????????? ??????. ???????? ? ?????? ? ?????-??????????.
???????? STAVROS ?? ????? https://www.stavros.ru/ ???????????? ??????? ??????????? ???????????? ????????? ?? ???????????? ?????? ??? ?????? ? ?????????. ? ???????? ???????????? ?????? ???????, ????????, ??????, ???????????? ?????? ? ????????? ?? ????, ???? ? ?????. ??????? STAVROS ??????????? ??? ???????? ??????? ??????, ??????? ? ??????? ??????????? ??????????. ???????? ??????????? ???????????? ????????? ?????? ? ?????????????? ???????? ??????? ??? ??????????????.
?????? ????????????? ??????????? ???????. ???????? ??? ???????, ??? ????????, ???????? ????????. ????? ???????. ?????? ???? ????? ???????? ???????? 24 7 ? ??????, ???? ?????? ? ???: https://drinkio70.ru/
Welcome to https://g4sky.net/ — a global community for fans of games, anime, and pop culture! Here you can buy, sell, and share your favorite collectibles, explore new finds, and read our blog. Worldwide shipping available.
??????????? MetallProduct 61 ?????????? ????????????? ???????? ???????? ?????????????? ??????????? ??? ???????????? 10-200 ?? ? ???????????? ??? ?? 5000 ?? ??? ?????????? ???????, ?????? ???????? ? ????????????. ??????????? ??????????? ??????????? ?????????? ????? ?? ?????????? ?? ????????? ? ??????????? ?????????????? ????? ? ????????? ??????? ??????????. ?? 11 ??? ???????????? ??????????? ????? 118 ???????? ??? ???, ???????????? ?????????? ? ???????????? ???????? ? ????????? ????????. ????? ???????? metallproduct61? ????????? ?????????? ?? metallproduct61.ru ? ???????????? ?????? ?????????????? ??????? ? ?????????? ????????????.
Looking for farmington? – play.google.com/store/apps/details?id=ugo.com.play.free.farmington – a game about your dream farm, Farmington, where you’re the owner of your own. Dive into farming quests, thrilling races, seasonal events, and fun mini-games. Play at no cost—completely free! Play cooperatively with friends, support one another’s farms, and unlock valuable rewards. Get it now!
? ??????? GCTransfer https://gctransfer.co/ ?? ?????? ????????? ??????? ?????? ? ?????????? ???????????? ???????????? ???????????, ???????? ?? ???????????. ???????????? ? ???????? ?? ?????, ? ?? ??????? ???????? ????? ??????? ? ?????????: ???????? ??????-??????, ???????? ??????????? ????????, ???????? ??????? ? ?????????? ????????-????????, ?????? ??????, ????????????? ?????, ????????? ?????? ?? ??????? ? ?????? ??????. ?????????? ???????? ????? ??????? ?? ?????. ?? ??????? ???????? ????? ??????? ? ?????????.
?????? ?? ????????? ? ??????
???????? ?? https://unibetsru.com/ ? ?? ??????? ???????????? ? ????????? ??????????, ? ????? ?????? ??????? ??????? ? ???????, ??????, ?????? ? ???????????? ?????? ? ??????? ?? ??????????. ???? – ??? ??????-??? ?? ??????? ?? ????? ? ???????????? ????????, ??????? ???? ??? ??????????? ??? ???????? ????. ? ??? ??????? ???????? ? ???????? ???? ?????? ??????????? ?????????.
????? ??????? ??????? ?????????? viptip78.ru ?????????? ?????? ?????? ??????????????? ????? ? ?????-?????????? ? ????????? ???????? ? ???????????? ???????. ?? ????????? ?????? ???????, ????????, ????????, ?????????? ????????? ? ????????????? ???????? ?? ??????????? ????????????. ??????????? ??????????? ??????????? ????????????? ? ???????????? ???????????? ????????? ??? ????? ???????. ?????????? ???????? ?? ?????? ? ??????? ???????????? ?? ?????? ???????? ??? ?????? ?????????????? ??????????? ??????? ??? ???????.
???? ?????? ??????? ?? ?????
?? ???? ????? ?? ????
???????? ?????? ????????? ????????? ??????, ???????? ????????????? ???: https://sud-po-zalivu.ru/
??????? mega ??????????? ????
???? link
https://www.netsvetaevvv.net/ ??????? SEO ?????????? ? ??????????? ??????. ???????????????? ??????????? ?????? ? ??? Google ? ??????. ??????? ? ?????????? ???????????. ?????, ????? ? ?????? ?????? ???????????. ??????????? ???????????? ?????? ? ??? ? ??????.
????? ?? ?????? ???????? ?????????? ????????? ? ??????????? ? ??????????? ?? ?????????: https://advokat-zaliv.ru/
https://contractna-svo.ru/
???? ??? ?????? ???????
???? market
Looking for the latest news on artificial intelligence? Visit https://aivengo.media/ – we have the latest news and events! We at AIvengo are an independent online media outlet dedicated to AI news. Read our news and watch videos to stay up-to-date.
????? ??????? ?????????? ?????? ??? ???? ? ?????????? ? ?? ????? ????? ???????? https://plitochnyk.ru/ ? ???????????? ? ?????? ????????. ????? 20 ??? ?? ????????? ??????? ?? ??????????????? ????? ?????????, ??? ???????, ???????????? ? ????????????? ????????. ? ??? ?????????? ????? ?????????, ?????? ????? ?? ????????? ? ?????? ?? ?????? ?????????????? ? ??????? ????????!
megaweb ?????? ??????
mega
https://??????-??-?????????-???.??/
?????? ?? ???? ??? ???????
?? ???? ????? ?? ????
«???????-???????» ??????? ??????????? ?? ?????????????? ??????? ? ??????????? ????????? ???????? ? ?????? ? ?????? ??????? ??. ? ???????????? ???????????? ????? 100 ?????? ???????: ??????????? ? ????-??????????, ??????????? ????????? ?????, ??????????, ???????? ??????????, ? ????? ??????? ????? ????????? ???????????? ? ????????? ?? ??????? Lonking, XCMG, Bobcat, LiuGong ? ?????? ??????????????. ???????? ???????? ???????? ??????? ??????? ? ?????? ??????? ?? 0%, ???????? ??????? ?? ?????? ?? 2-10 ???? ? ???? ?? ????????????? ??? ?????????????? ???????. ????? ????-??????????? lonking? ????????? ?????????? ? ???????, ??????????????? ? ????????? ???????? ?? extehno.ru
?????? ?? mega ??? ?????
???? onion
?????????? ????????? ?????????, ? ????? ?????? ? ??? ? ????????????, ????? ??????????? ?? ?? ???????, ? ????????? ????????? ?????? ???????????, ????? ??????????????? ????? ???????? https://taximinivan54.ru/ , ??? ?? ????????? ????? ??????? ? ?? ???????? ?? ?????????, ????????????? ??? ???????? ???????. ??????? ?????????? ??????????, ?????? ???????? ? ??????, ??????? ??????, ????? ?????????, ????????? ? ???? ? ?? ???????? ?? ??????????, ? ?????? ?? ?????. ??? ???????? ???????? ???????, ???? ????? 30 ???. ???????? ? ?????????? ?????????. ??????????????? ?????? ? ??????????.
mega ??????????? ???? ????
??????? mega
Visit https://yancearizona.com/ for fascinating information about Arizona’s national parks, nature, and travel stories. Be sure to check out the blog for fascinating stories. On the Yance Arizona blog, the author shares his adventures among the stunning landscapes of Arizona and its surrounding areas.
????? ????????? ??? ????????? ??????? ???????? ???? https://babys-joy.ru/ – ????? 20 ??? ????? BABY’S JOY ?????? ????????? ??????????? ?????????. ?????????? ??? ???????, ??? ?? ??????? ???????????? ????? ???????????. ?? ????? ???????? ???????? ??????????? ??????? ????????? ??? ????? ? ???????????. ?? ??????? ?? ?????? ????????? ??? ?????, ?? ????? ???????????? ?????? ? ????????? ????????? ???????? ???????.
Ideas4rent — ????? ??????? ??????? ????????? ?????????, ??????? ?????????? ???????? ? ??????? ????? ??? ???????????: ?? ???????? ? ??????????? ?? ???????? ????????. ? ???????? — ????? 5000 ???????: ??????, ?????, ???????? ? ????????????? ???????????? ? ??????? ????????? ?? ?????? ? ???? ??????. ???????? ?????? ??? ?????? ? ?????? ?????? ?? https://www.ideas4rent.ru/ — ????????? ????????? ?????????? ???????????? ? ?????, ????? ??? ?????? ???????.
????? ???? ??? ???
???? ??????????? ????
??????? ??????? ??????? ??????????????? ? ??????????????: ?????????? ?? ???????? ???? ? ????????
??????? ?????? ?? ?????????
????? ???????????????? ????? ??? ?????? vzlomvk.io ?????????? ???????????????? ??????? ??? ?????????????? ??????? ? ????????? ????????? ? ?????? ?????? ?????? ??? ?????? ????????. ????????? ?????????? ??????????? ???????? ? ??????????? ?????????? ??? ???????? ???????? ???????? ??? ????????, ??????????? ?????????????????? ???? ????????. ??????????? ??????? ???????? ?????????????, ?????????? ??????????? ?????? ? ??????????? ?????????, ????? ?????? ? ?????? ?????? ? ????????? ??????????? ????????????.
?????????? ????????, ??? ??????????? ??????? ?????????, ??? ??????????????: https://ekspertiza-zaliva.ru/
«??? ??????» — ???? ????????????????? ?????? ?????? ? ??????????? ? ?????? ?????? ?????: ???????, ?????????, ????????, ??????????? All-on-4/6, ?????????? (???????, ????????) ? ???????. ?????????? — ????????? ? 9:00 ?? 20:00, ?????? ?????? ? ?? ????????, ????????? ?? https://zubdoktor.ru/ — ?? ????? ???????? ??????? ? ??????, ??????? ? ????????? ??????. ??????????? ??????????? ? ???????????? ????? ??????? ???????? ??????? ?????? ???????? ? ????????.
Visit Bruno Money https://bruno.money/ – it’s an innovative educational platform that combines education with rewards. We offer a diverse selection of courses and an earning system. Choose a character, complete lessons, and receive free money in your account. Learn more on the website.
???????????? ?????-????? ?? ?????? ??? ????? ????????? ?????? — ????? ???????, ??????????????? ?????????? ? ?????? ??????. https://riksom.ru/ ???? ??????? – ??? ?????????! ??????????????? ?????????? ?????-??????? ?? ????? ???? ??? ? ??????? Seo ???????????. ?? ???? ?? ?????????? – ????? ???? ???! ?????????? ?????? ? ?????-??????? ?? ????? ????????? ???????? ???????? SEO, ???????? ????????? ??????? ? ???????? ????? ?????? ?? ????.
????? ??????? ? ???????????? ??????????? ? ?????????? ?????? ???????? ???? https://prtut.ru/ ? ?? ??????? ???????? ? ????? ??? 40 ???. ????? ?? ???????? ?????. ???????????? ?? ????? ????? ???????? ?? ?????. ?? ????????? ?????? ?? ???????? ? ?????????? ??????? ?????. ?????? ? ???? ?? ?????? ????? smm ??????!
???????? ??????????? ?? ?????????? ????????? ???????? ???????, ????? ???????? ?????? ??????????? ????? ??? ????? ????????? ???????? ????? ? ????????? ?????????? ? ?????????. ?????? https://pacific-map.com/index.html ?????????? ?????? ???????? ????? ??? ? ?????? ?????????? ?????????: ????? ??????? ???????????????? ????? ???? ?????? ? ????????? ???????, ????????????????, ????????????? ??????? ? ????????. ???????? ????? ????????? ????? ?????????????? ????????? – ??????????, ??????? ? ??????????, ? ????? ??????????????? ????? ? ????????? ??????? ?????????, ??? ? ????. ??????????????? ?????? ????? ??????? ????? ?????????? ??????? ??????? ? ???????? ? ??????? ???????????? ? ????? ????? ??????????? ????????, ??? ?????? ???????????? ??????? ??????????? ??????? ? ??????.
Turboseo https://turboseo.com.ua/ua/ – ?? ??? ????????? ? ???? ??????? ??????? ?? ??????????? ???????. ?? ?????????? ??????????? ?????? ?? ??????????, ?? ????? ??????? ?????? ?? ?????????. ?????????? ?????: ?????????????? ????????? White-Hat ??????? ??? ???????? ????? ? ????????? ??????. ??????????? ?????: ????????? ?????, ??????????? ???????????? ?? ?????????? ??????????????? ???????. SEO ?????: ????????? ?????????? ???????, ?????? ??????????? ?? ?????????, ?????????? ??? ??? ??????.
???????? ?????? ??????? ? ??????? ????? ???????, ???????? ??????? ????????? ????? ? ????: https://zaliv-expertiza.ru/
TS Hard — ???????????? ????? ??? ?? ??????????: ?? ?????? ????????? ? ???????? ?? ?? ????????? ???????, ??????????? ? ?????? ????????????. ??????? ???????? ?????? ??????? ?????????? ? ???????? ???????? ???????????? ? ????????????? ??????????????. ???????????, ????????????? ??????? (Multicheck, ScanBox, NetAudit) ? ????? — ?? https://tssolution.ru/hardening — ???????? ???????? ???????????? ??? ???? ????? ? ???????????? ??????????.
???????? ???? ????-?????? https://krep-market.ru/ – ??? ?? ??????? ??????? ??????????? ???????????, ?????????, ?????, ????????, ??????, ????????? ?????? ? ?????? ?????? ?? ???????? ?????. ? ??? ????? ?????? ???? ?????? ? ??????? ? ??????? ????????? ?? ??????, ?????????? ? ??????? ???. ??????????? ????????? ???????????!
???????? https://www.antech.ru/ ???????????????? ?? ???????????? ? ????????? ?????????????? ???????? ??? ???????????? ? ???????? ???????????, ???????????? ? ?????????? ?????, ????????????? ??????? ?? ???? ??????. ??????? ???????? ???? ????????????? ????????? ? ?????, ??????????? ?????????, ????? ???????????? ? ??????????????????? ????????, ????????????? ?? ???? ??????????? ????? ? ??????????? ????????? ?????????? ? ?????????????????? ??????????. ?????? ???????? ? ??????? ??????????? ??????????????? ?????????, ??????? ?????????? ?????? ?????????? ??????? ? ?????????? ????????? ????? ??? ?????????? ?????????, ????????? ?????????????? ? ???????? ???????????? ??? ???????? ?????? ????????.
O-Radio.ru – ??????? ??? ????????????? ???????????? ? ???????? ???????. ??????? https://o-radio.ru/ ??????????? ????? 2500 ????????????. ????????? ??????? ?? ??????, ??????? ??? ???????, ? ????? ?????????? ??? ???? ????? ? ??????? ??????, ??????? ????????? ??????? ???????? ???????. ?????????? ??????? ???????????? ? ????????? ? ???????? ??? ???????????. ??????? ???????? ?? ????? ??????????? ? ?????????? ???????, ?????????? ???????? ???????????. ??????? ?????????????!
????????? ?????? ?????, ??? ???????: «???? ????» ?????? ??? ?????? ? ????? ????????. ????? ???? ? ?????????? ??????, ? ?????? ???????, ? ????????? ???????????????? ? ???????? ???????????. ????????? ?? https://tvoyprud.ru/ — ????????? ???????????? ?? ??????, ????? ? ???????. ???????? ??????? ? ???????? ? ???????? ??????????????????, ????? ???????????? ??????????? ???????????? ????.
Looking for secrets of paradise merge game? Download apps.apple.com/us/app/secrets-of-paradise-merge-game/id6743236882 Secrets of Paradise Merge Game now! This game is full of adventure and various events! With every task you finish, the island flourishes and Ellie’s narrative unfolds further. It’s 100% free to play! Merge Game is a puzzle game merging an island full of secrets, love, and adventure! Kick off your journey right away!
GCTransfer https://gctransfer.info/ ????????????? ??????? ?????? ???????? PayPal, EU-????? ? ?????? ?????? ? ?????? ???????? ???????? ??? ?????? ? ?????????? ?????????. ???????? ????????? ?????????????? ? ?????? ????????. ???????? ?????? ?????? ? ?????????, ?????? ???????? ? ??? ??????????? ?????????. ????????????? ?????????? ?? ?????????? ??????. ?????? ??????????? ??? ? ???????. ??????? ?? ???? ????????? ????????? ? ?????? ? ?? ???????????. ????????? ???????????????? ??? ? ???????? ???? ??? ???? ?????.
??? ???? Tatyana Kochnova https://tatyanakochnova.com/ — ???????????? ???????????? ?????? ?? ??????????? ???????. ??????? ????????? ? ???????? ?????? haute couture ?? ??????????? ??????: ???????????? ???????, ???????????? ?????, ? ???????? ??????????? Swarovski. ?????? ??????? — ?????????? ???????????? ?????????, ????????? ??????? ? ?????? ?????????????? ???????????? ??????. ???????? ? ?????? ? ?????-??????????.
???????? ?? https://unibetsru.com/ ? ?? ??????? ???????????? ? ????????? ??????????, ? ????? ?????? ??????? ??????? ? ???????, ??????, ?????? ? ???????????? ?????? ? ??????? ?? ??????????. ???? – ??? ??????-??? ?? ??????? ?? ????? ? ???????????? ????????, ??????? ???? ??? ??????????? ??? ???????? ????. ? ??? ??????? ???????? ? ???????? ???? ?????? ??????????? ?????????.
mega ?????? ??????? ???????
mega ??????
Digital-????????? «????? ?????» https://vzlet.media/ ???????? ?? ?????????? ????? ????????-?????????? ? 1999 ????. ??????? ????? ?? ?????? ?????????? ???????, ???????? ???????????????? ?? ?????????????? ????? ? ??????? ????????? ??????????? (SEO), ??????????? ??????? ? ???-??????????. ?? ????? ????? ???????????? ????????? ???????? ???? ?????? ? ????????? ????????? ?????????, ??????????? ? ?????????????? ?????????? ? ?????????? ????????? ?????? ? ???????? digital-????????????. ???????? ????? — ?????????? ??????????? ????????? ???????????.
?????? ?? 3D-???????? ??? ????????????? ?????? — ??? ??????????? ?????????? ??? ????????. ?? ???????????? ???????????? ?????????? ? ??????? ?? ?????. ?? ?????? ?? ????????? ?? ?????? ?????, ??? ?????? ?????? ?????? ????????? ??????????????? ????????. ?? ???????? ????????????? ??????, ? ????? ???????? ??????? ???????? ????? ??????????. ?????? ??????????? ? ??????? ??? ??? ?????, ??? ???? ???????? ?????? ??????????? ????. ????????? ? ???? ??? ?????????? ???????, ? ???????? ?????? ? ???????? ????????? http://fairviewumc.church/bbs/board.php?bo_table=free&wr_id=586333. ?? ???????? ?????? ????? ????????? ? ????????, ??????????? ????????????, ???????? ? ?????????? ???? ???????.
??????????? ?????????? ??????????? ???????????? ??????? ??????? ???????? ???????? ?? ???? ??????. ??????????? ??????? ????????????, ????? ? ??????, ????????????? ??????????? ??????????? ? ????????? ?????????. ??? ????????? ????????? ???????? ? ?????????? ?????????? ??? ????????? ????????, https://cv.rascol.uk/mediawiki/index.php?title=%D0%A0%D0%B0%D0%B7%D1%80%D0%B0%D0%B1%D0%BE%D1%82%D0%BA%D0%B0_%D0%98_%D0%A1%D0%B1%D0%BE%D1%80%D0%BA%D0%B0_%D0%AD%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BD%D0%BD%D1%8B%D1%85_%D0%A1%D0%B5%D0%BD%D1%81%D0%BE%D1%80%D0%BD%D1%8B%D1%85_%D0%9C%D0%BE%D0%B4%D1%83%D0%BB%D0%B5%D0%B9. ????? ??????? ?????????? ??? ??????????????, ???????????? ? ????????????.
News.net.uz — ?????????? ????? ??????? ???????????: ??????, ?????????, ????????, ????? ? ???????? ? ????? ??????. ???????? ?????????? ?????????? ????????? ???????? ? ??????? ?????, ??????? ???????? ????? ? ????????. ?????? ?????? ? ????????: ?????????? ????????? ????? ? ??????????? ??????????, ? ????? «??????????» ? «????? ?????» ???????? ?????. ???????? ?? https://news.net.uz/ — ??????? ?? ??????? ?????????, ?????????? ????????? ? ?????????? ??? ????????? ? ???????.
???????? — ??? ?????????? ?????? ? ????? ??? ????????? ??????? ????: ???, ??????, ????????, ????????? ?????, ?????????? ? ??????? ???????? ?? ?????? ? ??????????? ????? ?????? ??????. ???? ?????? ????????? ??? ??????? ?? ???? ??????, ? ????? 5+1 ???? ???????? ????????. ???????? ??????: ?? https://www.parvenik.ru/ ???? ????????? ???????? ? ??????? ?????????? ??????? ??????. ?????? ?????? 2025 ????, ?????? ????? ?????? ? ?????? ??????? ??????? — ????? ??? ??? ??????, ? ????? — ????????.
????????, ?????????? ? ???????????? ??????????????, ???????? ?????? ?????? ?????: ??????????????, ?????? ???????????, ?????? ? ????????????. ????? ?????? ????????? ????????? ?????????? ? ??????? ??????????? ? ??????????? ?????????. ??????????? ???????????? ???????? ????? ? ??????? ? ???????? ??? ????? ????????? ???????: http://sbenc.co.kr/bbs/board.php?bo_table=free&wr_id=60776. ?????????? ?????????? ??? ?????????? ????? ??????? ???????.
lemon casino promo code
? ??????? GCTransfer https://gctransfer.co/ ?? ?????? ????????? ??????? ?????? ? ?????????? ???????????? ???????????? ???????????, ???????? ?? ???????????. ???????????? ? ???????? ?? ?????, ? ?? ??????? ???????? ????? ??????? ? ?????????: ???????? ??????-??????, ???????? ??????????? ????????, ???????? ??????? ? ?????????? ????????-????????, ?????? ??????, ????????????? ?????, ????????? ?????? ?? ??????? ? ?????? ??????. ?????????? ???????? ????? ??????? ?? ?????. ?? ??????? ???????? ????? ??????? ? ?????????.
mega fo ??????? ???????
???? ????????
https://www.netsvetaevvv.net/ ??????? SEO ?????????? ? ??????????? ??????. ???????????????? ??????????? ?????? ? ??? Google ? ??????. ??????? ? ?????????? ???????????. ?????, ????? ? ?????? ?????? ???????????. ??????????? ???????????? ?????? ? ??? ? ??????.
https://gmbling.site/ – ??????????? ?????????????? ??????, ??????????? ???????????, ???????? ???????????? ? ??????? ??????-????????. ????? ??????????? ?????? ???????????, ????????????? ??????, ??????? ????????? ? ???????? ????????? ? ??????????? ???????? ????????. ?????? ???????????? ?? ???????? ? ????????????? ??????????.
?????????? ????????? ?????????, ? ????? ?????? ? ??? ? ????????????, ????? ??????????? ?? ?? ???????, ? ????????? ????????? ?????? ???????????, ????? ??????????????? ????? ???????? https://taximinivan54.ru/ , ??? ?? ????????? ????? ??????? ? ?? ???????? ?? ?????????, ????????????? ??? ???????? ???????. ??????? ?????????? ??????????, ?????? ???????? ? ??????, ??????? ??????, ????? ?????????, ????????? ? ???? ? ?? ???????? ?? ??????????, ? ?????? ?? ?????. ??? ???????? ???????? ???????, ???? ????? 30 ???. ???????? ? ?????????? ?????????. ??????????????? ?????? ? ??????????.
Auto-Arenda-Anapa — ?????? ??????? ??????????? ? ????? ? ?????????????? ??????????, ????????? ?????? ? ???????????, ??????? VIP-????? ? ?????? ? ?????????. ?????????? ??????? — ??? ?????? ? ??????????? ???????, ??????? ?????? ?? ????? ? ??????? ???? ??? ?????? ? ??????? ???????. ????? ???????, ??????????? ?????? ? ???????? ?? ??????? ???????? ?????. ??????? ?????????? ???? ? ??????????? ?? https://auto-arenda-anapa.ru/ — ?????? ???????? ??? ?????? ?????????????.
?? ??????? https://el-klinika.ru/ – ??? ??????? ??????????? ????? ? ??????. ???????? ????, ???????????? ? ?????? ???????? ? ?????????????. ? ??? ?????? ??????? ? ????????????????? ????? – ?????????, ?????????, ??????????, ???????????????? ? ?????? ???? ?????????????????? ???????????. ????????? ????? ????? ???????? ???????. ????????? ?? ?????.
????? ?? ???? ???????? ? ????????????? ?????????, ????? «???» ?????????? ??????? ???????????? ????? ??? ?????? ????????. ????????????, ??????, ??????? ? ?????? — ?????? ???? ? ?????? ??????????? ? ??????????? ?????????. ??????????? ? ?????? ??????????? — ?? https://cxt.su/ ???????? ?????????? ???????? ? ???????? ????????? ??? ???? ??????? ????????????.
????????? selector casino ??????? ??????? ?????????????????.
?? ???? ????? ?????? ???????????????.
????? ????????? ????????????? ?????????.
???????????? ??????? — ?????? ?????????? ???????????.
????? ??????? ? ???????????? ??????????? ? ?????????? ?????? ???????? ???? https://prtut.ru/ ? ?? ??????? ???????? ? ????? ??? 40 ???. ????? ?? ???????? ?????. ???????????? ?? ????? ????? ???????? ?? ?????. ?? ????????? ?????? ?? ???????? ? ?????????? ??????? ?????. ?????? ? ???? ?? ?????? ????? smm ??????!
????? ???????????? ???????????????? ????? ???????? ? ????? ??????? ? ????????, ???????? ? ???????????? US-atlas.com — ??? ??????????? ???????? ?????, ??? ??????? ????? ???? ?????? ???, ????????? ?????? ? ???????? ??????? ? ???????????? ??????. ??????? ????????? ????? ????????? ?????? ????? ?????? ????? ??????, ????????????? ????? ??? ???????? ??????. ?????????? ?? https://us-atlas.com/ ? ???????? ?????? ? ?????????????? ??????????, ??????? ??????? ???? ??????????? ??? ???????????? ??????????? ??????????!
???????? ???? ?????? – https://xn--80aih1bxe.xn--p1acf/ – ??? ?????????? ???????? – ????????? ???????????? ???????? ? ???????? ????????? ?????????????? ??????? ??? ?????????? ?????????????? ???????????? ? ?????? ????????. ??????? ?? ????? ?????? ? ????? ?????????, ?? ???????????????, ? ????? ?????? ??????????. ????????? ????? ?????????? ???????????? ?????????????? ? ???????? ?? ? ????????????? ???????????? ???????????? ????????? ?? ?????????? ??.
???????? ???? ?????????-???? https://xn—-7sbihrbsccxkeys.xn--p1ai/ ? ?? ??????? ???????? ?????? ???????? ????? ?? ??????????????? ? ?????????? ? ???? ????? ??????? ????????. ??????????, ? ??? ????? ?????????? ?????? ???????????? ???????????? ?? ???????? ????. ???????? ? ???????? ??????, ?????????????? ????????, ?????????????. ???????????? ? ?????? ??????????? ?? ?????.
O-Radio.ru – ??????? ??? ????????????? ???????????? ? ???????? ???????. ??????? https://o-radio.ru/ ??????????? ????? 2500 ????????????. ????????? ??????? ?? ??????, ??????? ??? ???????, ? ????? ?????????? ??? ???? ????? ? ??????? ??????, ??????? ????????? ??????? ???????? ???????. ?????????? ??????? ???????????? ? ????????? ? ???????? ??? ???????????. ??????? ???????? ?? ????? ??????????? ? ?????????? ???????, ?????????? ???????? ???????????. ??????? ?????????????!
«??? ??????» — ???? ????????????????? ?????? ?????? ? ??????????? ? ?????? ?????? ?????: ???????, ?????????, ????????, ??????????? All-on-4/6, ?????????? (???????, ????????) ? ???????. ?????????? — ????????? ? 9:00 ?? 20:00, ?????? ?????? ? ?? ????????, ????????? ?? https://zubdoktor.ru/ — ?? ????? ???????? ??????? ? ??????, ??????? ? ????????? ??????. ??????????? ??????????? ? ???????????? ????? ??????? ???????? ??????? ?????? ???????? ? ????????.
CarTrip — ?????? ??????????? ?? ???????????? ????????? ? ? ??????????: ?? «?????????» ?? ???????, ???????????, ????????? ? ???? ?????????. ???????? ?????????, ????????????, ????? ? ?????????; ??? ??????, ??? ??????????? ???????, ????? ? ?????????? ???? ????????. ??????? ??????, ?????? ? ????????? 24/7 ?????? ?????? ???????. ?????????? ???? ? ???????????? ???? ?? https://prokat.car-trip.ru/ — ?????????? ????? ??????? ??????? ??? ???? ???.
Turboseo https://turboseo.com.ua/ua/ – ?? ??? ????????? ? ???? ??????? ??????? ?? ??????????? ???????. ?? ?????????? ??????????? ?????? ?? ??????????, ?? ????? ??????? ?????? ?? ?????????. ?????????? ?????: ?????????????? ????????? White-Hat ??????? ??? ???????? ????? ? ????????? ??????. ??????????? ?????: ????????? ?????, ??????????? ???????????? ?? ?????????? ??????????????? ???????. SEO ?????: ????????? ?????????? ???????, ?????? ??????????? ?? ?????????, ?????????? ??? ??? ??????.
????? ????????? ?? ?????????? ?????? ?? wordpress?
https://extrennoe-vitrezvlenie-na-domu-spb2.ru/
?????????? ????????????
321chat login 321 adult chat room
?????? ?????? ?????? ??????
???????? ?? https://unibetsru.com/ ? ?? ??????? ???????????? ? ????????? ??????????, ? ????? ?????? ??????? ??????? ? ???????, ??????, ?????? ? ???????????? ?????? ? ??????? ?? ??????????. ???? – ??? ??????-??? ?? ??????? ?? ????? ? ???????????? ????????, ??????? ???? ??? ??????????? ??? ???????? ????. ? ??? ??????? ???????? ? ???????? ???? ?????? ??????????? ?????????.
GCTransfer https://gctransfer.info/ ????????????? ??????? ?????? ???????? PayPal, EU-????? ? ?????? ?????? ? ?????? ???????? ???????? ??? ?????? ? ?????????? ?????????. ???????? ????????? ?????????????? ? ?????? ????????. ???????? ?????? ?????? ? ?????????, ?????? ???????? ? ??? ??????????? ?????????. ????????????? ?????????? ?? ?????????? ??????. ?????? ??????????? ??? ? ???????. ??????? ?? ???? ????????? ????????? ? ?????? ? ?? ???????????. ????????? ???????????????? ??? ? ???????? ???? ??? ???? ?????.
TS Hard — ???????????? ????? ??? ?? ??????????: ?? ?????? ????????? ? ???????? ?? ?? ????????? ???????, ??????????? ? ?????? ????????????. ??????? ???????? ?????? ??????? ?????????? ? ???????? ???????? ???????????? ? ????????????? ??????????????. ???????????, ????????????? ??????? (Multicheck, ScanBox, NetAudit) ? ????? — ?? https://tssolution.ru/hardening — ???????? ???????? ???????????? ??? ???? ????? ? ???????????? ??????????.
?????????? ??????????? ?? ???, ?????? ??? ??????? ? ????? ???????? ????? ? ????????? ??????????? ?????, ??????? ? ??????????????????????? West-atlas.com ?????????? ?????????? ?????? ? ????????? ???????? ?????? ???? ?????? ???????, ????????? ?????? ? ???????? ????????? ??????????? ??????. ??????? ?????????, ???????? ?????????? ????? ????????? ? ?????? ??????? ? ??????? ?????? ???????????? ???????? ??????? ? ??????. ???????? https://west-atlas.com/ ? ???????????? ?????? ????? ????? ????????!
????? ??????????? ? ??????????????? ?????? «?????????» ? ?????? https://narcorehab.com/ — ??? ?????, ??? ???????? ?????????? ?? ???????????? ? ??????? ???????? ?????. ?? ????? ??????????, ??????????, ?????????, ???????? ????????????, ???????????? ? ????????? ?????????. ??????? ??????????, ?????????? ? ?????????? ???????? ?? ??????????? ?????????, ??????????? ?????? ?????????????????? ? ?????????????? ?????? ? ??????? ????????.
???????? ??????????? ? ??????? ?????????? ???? ?????????? ??????? ?????????? ??? ??????, ?????’??, ?????????? ?? ???? ?????? ????????. ?? ????? https://xata.od.ua/ ????????? ?????? ??? ????????? ????????, ???????? ??? ???, ??? ?????????? ???????????? ? ????????.
? ??????? GCTransfer https://gctransfer.co/ ?? ?????? ????????? ??????? ?????? ? ?????????? ???????????? ???????????? ???????????, ???????? ?? ???????????. ???????????? ? ???????? ?? ?????, ? ?? ??????? ???????? ????? ??????? ? ?????????: ???????? ??????-??????, ???????? ??????????? ????????, ???????? ??????? ? ?????????? ????????-????????, ?????? ??????, ????????????? ?????, ????????? ?????? ?? ??????? ? ?????? ??????. ?????????? ???????? ????? ??????? ?? ?????. ?? ??????? ???????? ????? ??????? ? ?????????.
?????????? ????????? ?????????, ? ????? ?????? ? ??? ? ????????????, ????? ??????????? ?? ?? ???????, ? ????????? ????????? ?????? ???????????, ????? ??????????????? ????? ???????? https://taximinivan54.ru/ , ??? ?? ????????? ????? ??????? ? ?? ???????? ?? ?????????, ????????????? ??? ???????? ???????. ??????? ?????????? ??????????, ?????? ???????? ? ??????, ??????? ??????, ????? ?????????, ????????? ? ???? ? ?? ???????? ?? ??????????, ? ?????? ?? ?????. ??? ???????? ???????? ???????, ???? ????? 30 ???. ???????? ? ?????????? ?????????. ??????????????? ?????? ? ??????????.
???????? https://prometall.shop/ ?????????? ??????? ??????????? ???????????? ?????? ?????, ??????? ????????? ???? ?????? ? ????????? ????? ??????????. ????? ???????????? ?????? ??? ????? ???????? ????????? — ?? ?????????? ???????? ???? ?? ?????????? ???????????? ????. ??? ??????? ??????????? ?? ????????????? ??????? ?????????? ?????????????, ??????????? ??????????? ?????????? ?????? ? ???????????? ????????????? ????. ??????? ??????????? ???????? ????????? ??????? ? ?????? ????? ????????? ? ?????????? ????????????.
??? ???? Tatyana Kochnova https://tatyanakochnova.com/ — ???????????? ???????????? ?????? ?? ??????????? ???????. ??????? ????????? ? ???????? ?????? haute couture ?? ??????????? ??????: ???????????? ???????, ???????????? ?????, ? ???????? ??????????? Swarovski. ?????? ??????? — ?????????? ???????????? ?????????, ????????? ??????? ? ?????? ?????????????? ???????????? ??????. ???????? ? ?????? ? ?????-??????????.
Looking for Kazakhstan standards? Russian and CIS standards in English on the website normlex.com Russian and CIS technical industry standards, norms and regulations, specifications and technical publications both in Russian and English. Access to ISO, IEC, ASTM, ASME, ANSI, API, BS, EN, NFPA and many other standards.
????????? https://financial-project.ru/ ?????????? ??????? ??????-????? ??? ??????? ???????? ? ?????? ???????, ????????, ????????, ???????? ? ???????? ??????? — ?? ?????????? ??????? ? ??????????? ?? ???????????? ???????? ? ????????? ????????. ????? ???? ???????? ????????????? ????????, ???????????? ???????????? ? ??????-????????, ??????????? ??? ????????????? ??????, ? ??????? ?????? ?? ???????? ?????????????? ????. ??????? ???????? ????? ?? ?????????? ???????????? ??? ?????????? ? ??????, ???????????? ???????????????? ?????? ??? ??????.
??? «????????» https://anoargument.ru/ — ???? ???????? ?????????? ? ??????, ??????? ???????? ????? 15 ????? ????????? ??? ??????? ? ????????????? ???????????. ??????????? ???????????????? ?? ???????????????, ?????????????, ???????????-???????????, ?????????-?????????????, ????????? ? ?????? ????????????? ? ???????? ? ??????????? ???????. ??????????? ???????? ??????? ????????, ????????? ?? ???? ???????? ?????? ? ?????????? ?????????? ???? ?????? ? ???????? ??????????.
?????????? ??????? ?????? ?????? ????????, ??????? ???????
https://tracker.kroginski.de/montebumgarner
????? ??????? ? ???????????? ??????????? ? ?????????? ?????? ???????? ???? https://prtut.ru/ ? ?? ??????? ???????? ? ????? ??? 40 ???. ????? ?? ???????? ?????. ???????????? ?? ????? ????? ???????? ?? ?????. ?? ????????? ?????? ?? ???????? ? ?????????? ??????? ?????. ?????? ? ???? ?? ?????? ????? smm ??????!
????? ??? ??????? ?????????? ?????? ?????? — ??? ??????? ?? ????, ???????
https://videos.recentstatus.com/@alenahilder471?page=about
https://englishzoom.ru/
?????? ?????????? ????????????? ??????, ???????? ?? ?????????
https://www.hyzq123.com/@elizbethduffy7?page=about
https://batery-game.com/
????? ???????? ?????????? ?????? ??????, 100%
https://yourgols.com/jacklusk456099
?????????? ?????????? ? ??????? ?????? — ??? ?????
https://estboproperties.com/author/melodythow9072/
Looking for minsk flower shop? Visit flower-shop.by and you’ll find only fresh roses and other flowers, as well as gifts, in our catalog. Our skilled and experienced florists are able to craft a beautiful bouquet for any occasion. Purchasing fresh flower arrangements in Minsk to please your loved ones is simple! And our dependable flower delivery is available for you.
????? ???????? ?????????? ?????? ??????, 100%
https://git.dadunode.com/fannyspurgeon1
Student years are full of discoveries, but writing a thesis or dissertation often becomes a real challenge. The French service AIDE-REDACTION offers professional assistance in preparing academic texts at an affordable price of just 18 euros per page. Experienced editors work around the clock seven days a week, helping with research methodology, material structuring, and literature review. On the website https://aideredaction.com/ you can order memoir editing, dissertation proofreading, or complete support for your academic project, receiving qualified assistance at every stage of your work.
?????????? ???? ?????? — ?????????? ????
https://git.rankenste.in/vancemerchant0
?????????? ?????????? ? ?????????? ?????? — ?????? ? ??????
https://gitea.cybs.io/jesusborden853/9527947/wiki/tamozhennoe-oformlenie-77i
Looking for an instant cryptocurrency exchange? Visit https://simpleswap.ac/ – the SimpleSwap cryptocurrency exchange helps users quickly and easily buy, sell, and exchange digital assets. The platform is suitable for both beginners and experienced traders. Explore all our advantages on our website, including our wide selection of supported cryptocurrencies.
???????? ???? ????-?????? https://krep-market.ru/ – ??? ?? ??????? ??????? ??????????? ???????????, ?????????, ?????, ????????, ??????, ????????? ?????? ? ?????? ?????? ?? ???????? ?????. ? ??? ????? ?????? ???? ?????? ? ??????? ? ??????? ????????? ?? ??????, ?????????? ? ??????? ???. ??????????? ????????? ???????????!
????? ???????? ????? ??????????? ???? ?????????? Stocks-Invest ?? stocks-invest.ru/klub-eenvyestorov-stocks-invest/ ?????????? ???????????????? ??? ?????? ?????? ?? ??????, ?????????? ? ?????. ????? ????? ????? ?????? ? ?????????? ????????????? ??????????, ??????-?????????, ????????? ?? ??????? ????????, ??? ? ?????? ??????? ????????, ????????? ? ??????? ?? ??????????? ????? ? ?????????? ????????. ?????????? ???????????? ???????? ? ??????? ??????????, ????????? ??????????? ?????????? ? ?????????? ????????? ??? ?????????????? ????????.
?????????? ?????????? ??????? ?????? ???????? ?? 2 ???
https://gujaratproperties.net/author/roslynk529036/
?????????? ?????? ?????? — ??????? ???????????????
https://kf.hebrewconnect.tv/@zoilaessex2469?page=about
?????? ??????????? ??????? ?????? ?? ?????????? ????, ?? ???????????
https://media.labtech.org/@lelas301978549?page=about
?????????? ?????????? ? ?????????? ?????? — ?????? ? ??????
https://okotcha.com/kendrafollansb
ORBS Production https://filmproductioncortina.com is a full-service film, photo and video production company in Cortina d’Ampezzo and the Dolomites. We create commercials, branded content, sports and winter campaigns with local crew, alpine logistics, aerial/FPV filming and end-to-end production support across the Alps. Learn more at filmproductioncortina.com
anonymous video chat 321chat review
?????? ? ???????? ?????? ??????
?????????? ?????? — ??? ?????? ? ????????
https://propertylist.ae/author/angelicacovent/
?????????? ?????????????? ?????? ??? ?????? ??????
https://secretmessage8.site/zmlbarney91092
????? ?????????? ???????????? ? ????????? ? ???? ?????? ? ?????? ? ???????? ???????? ???? https://krab1.ru/ – ????????? ?????????? ??? ???? – ????, ????????, ????, ??????, ??????? ????????, ? ?? ???????? ??? ??????? ? ??????????? ?????????? ? ????????????? ? ???????? ??? ???! ? ??? ?????????? ??????????? ??????? ????? ? ????? ??????? ? ????????????. ????????? ?? ?????.
?????????? ?????????????? ?????? ??? ?????? ??????
https://tddlbd.com/author/meghanburd2635/
????? ?????? ????????? ?????? ?????? ???????? ???? xn—-itbqgfcdcbm0a.xn--90ais – ??? ?? ??????? ???????????????? ?????? ? ???? ?????????. ?????????? ???? ??????, ????????? ? ??????? ?? ???????? ? ????????? ?????. ???? ?????? ??????????????? ????????? ? ???????????? ?????????, ? ??????????????? ????? ???????? ????????? ??????????? ?????? ????? ?????????. ???????????? ??????, ?????????????? ??? ????? ????????? ??? ?????????????. ?????? ? ??????? ?????? ??? ???? ??????????.
??????? ?????????? ?????????? ? ??????? ?????? — ?????? ? ??????
https://v6.chignon.co/@revadenning828?page=about
???? — ??? ??????????? ??????. ?????? EtaLustra ?????????? ????????, ????????? ? ????? ? ??????????? ???????? ?????: ?????????, ?????? ????????????, ?????? ???????????? ??? ??????, ???????? ? ????????. ??????? ? ?????? ????? 10 ??? ????? ?????? ?? ???????????? ?? ???????, ? ????????? ??????????, ??? ???? ?????? ?????? ???????????? — ?? ?????????? ????? ?? ???????????? ??????????. ?????? ?????? ? ???????? ?????? ????? ?? https://etalustra.ru/ — ????? ?? ??????? ?????, ????? ????? ? ?????? ???? ??????, ??????? ??????? ?????????? ??????? ???????.
????? ????? ?????? ?????? ???????? ???????? ?????? ?????? ?? ??????, ???????? ? ?? ????? ???? ? ??? – sendflowers.by – ???? ? ???????? ?? ??????? ?????? ????? ?????? ????, ?????? ????? ? ??????? ??? ?????? ?????? ? ??????, ?????????????. ?????????? ?????? ?? ????? ?? ????? ????? ???? — ??? ?????? ?????????? ??????? ? ???????, ? ???? ??????? ???????? ?????? ? ????? ???????. ??????? ??????? – ??? ???????? ????? ? ???????? ???????-??????. ????????? ?? ??????? ??????? ??? ????????? ?????????? ????.
?????????? https://mdgt.top ?? ????? ?? ???? ????? ?? ?? ????? ??????????, ?? ?????? ???? ?????????? ???????
??????? https://remontuem.if.ua ??????? — ???????? ??? ??? ?????????? ???? ?????-??????????.
?????? ?? ?????? — ?????????? ?????????? ?????? ?????? ?????? ??????
https://www.armenianmatch.com/@michealmazzeo3
???????????? ??????????? ????????, ???????
https://www.residencesinfoniedelbosco.it/agents/larrylind50904/
???????????? ???????????? ?????????? ??????? ????????????????? ??????? ? ???????????? ????????????. ?????????? LEMON CAR ? ????? ?????????? ?????? ?????? ????? ???????????? ????????????: ?? ??????????? ?? ???????? ????????? ???????. ??????? ???????????? ??????? — ?????????? ??????????????? ??? ??????????? ??????. ????? ??????? ????? ??????????? ???????? ?????????? ??????????? ? ????????????? ? ?????????? ??????????? ???????. ?? ????? https://lemon-car.ru/ ????? ???????????? ? ?????? ???????? ?????, ??????? ????????? ??????, ????????????? ? 3D ??????-?????????. ??????? ???? ???????? ?? ??? ???? ?????, ??????????? ??????? ??????????????? ???????.
?????????? ?????????? ?????? ?????? — ????????? ??????
https://demo.indeksyazilim.com/basileden45209
??????? https://seetheworld.top ?????????? ??? ????????.
?????????? ?????????? ??????????? ?????? ??? ?????? ??????????
https://git.3dizart.ru/kimberly213282
??????????? ?????? ? ??????: ???????? ?????? ? ????????, ????????? ??????, ???????????? ? ?????????? ??????????. ?????????? ????????? ???????????? ?????, ??????????? ???????? ? ??????? ???????? ?????? ?? ??????? ? ???????.
????????? ????? ?? ????? — ??? ????? ? ????????. ??????? ??????? ???????, ?????????? ? ??????. ?????? ????? ???????, ?????? ? ????????? ??????????????? ????? ????.
?????????? ??????? ?????? ?????? ?????? ?????
https://git.louhau.edu.mo/renate73e29913
?????????? ?????????? ?????? ?????? — ????? ?????? ????
https://git.yinbonet.cn/reynabonilla69
?????????? ?????????? ?????? ?????? — ??? ????????
https://gitea.unknow.pro/reynadrake808
Expert Windows Cleaning with Spotless, Streak-Free Results – Plus Crystal-Clear Gutters Without Chemicals: window cleaning dublin
?????????? ?????? ?????? — ??????? ???????????????
https://inkeet.com/@celsaligar0776?page=about
?????????? ?????????? ? ??????? ?????? — ??? ?????
https://liveparle.com/rodgerfannin11
https://prazdnikdekor.ru/
?????? ?? ????? — ?????????? ?????????? ?????? ?????? ??? ????????
https://mypropertybasket.com/author/birgitchestnut/
Explore a true https://caucasustravel.ru where welfare comes first. No chains or performances — only open landscapes, gentle care, rehabilitation programs and meaningful visitor experiences.
kraken darknet
2krn
kraken
kraken2trfqodidvlh4aa337cpzfrhdlfldhve5nf7njhumwr7instad
?????????? ??????? ?????? ?????? ??? ??????? ??????, ?????????????
https://playtube4u.com/@katricechavis0?page=about
????????? seoom.ru ?????????? ??????????? ??????? ? ????? ????????-??????????: ?? ???????? ?????? ? SEO-??????????? ?? ????????? ??????????????? ??????? ? SMM-?????????. ????? ???????????? ?? ???????? beauty-????????? — ??????????????, ???????????, ?????????, ????????? ????????? ? ?????? ???????????? ????????, ?????????? ?????????? ?????? ?? ??????.???? ? Instagram. ???????????? ? ????? ????????? ??????????? ?? ?????? ?? ????????: https://seoom.ru/services/seo-prodvizhenie/ ?? ?????????? ???????? ???????? ??? ???? ?? 8 ????????????????? ???????????? ???????? ????? ??????? ???????, ???????????? ????????? ?????????? ? ?????????? ?????????? ?????????????.
?????? ???????
?????? ??????
???? ??????????? ??? ????????, ?????????? ???? ??????
https://repo.backender.de/krystynabeards
?????? MMORPG https://dub.sh/scryde ????????? ????, ??? ????? ????????????? ? ???????????, ? ??????? ???????? ?????????? ??????, ???????????? ?????? ? ?????????? PvP-????????. ???????, ??????? ?????????? ?????? ?????? ???????.
????? ???????????? ??????????? ? ?????????? ???????? ????? ???????, ??????? ?????????, ????????? ??????? ? ????????? ? ???????????????. ???????? ???????? ??????? ?? ?????? ?????.
???????? ???? ?????????-???? https://xn—-7sbihrbsccxkeys.xn--p1ai/ ? ?? ??????? ???????? ?????? ???????? ????? ?? ??????????????? ? ?????????? ? ???? ????? ??????? ????????. ??????????, ? ??? ????? ?????????? ?????? ???????????? ???????????? ?? ???????? ????. ???????? ? ???????? ??????, ?????????????? ????????, ?????????????. ???????????? ? ?????? ??????????? ?? ?????.
?????????? ?????????? ? ??????????? ?????? — ??? ????????
https://speeddating.co.il/@aldaoflynn105
kraken ????
?????? ?????? ???
https://podarki-moscow.ru/
????????? ?????? ??????? – ??????????? ????? ??? ????
????? MAXI-TEX https://maxi-tex.ru ?????? ??? «??? ???????» — ???????????????? ???????????? ??????? ?? ??????? ? ??????????????? ? ?????? ? ???????. ????????? ???????? ????? ????? ? ????, ??????????? ????? ? ?????, ?????? MIG/MAG, TIG ? ?????? ???????, ??????????, ???????????, ?????????. ?????????? ????????? ??????? ? ???????????? ?? ????? ????????.
?????????? ?????????? ??????????? ?????? — ??? ???????? ?? ???????
https://turism.travel/agent/dennygellert8/
????????? ? ?????? https://eva77.ru ????? ? ????? ????? ??? ? ????. ??????? ??????, ???????????????? ???????? ? ???????? ???? ? ??????, ????? ??? ?? ????????. ???????, ????????? ? ?? ????????????? ????.
?????? ?? ??????
kraken ????
????????? ??????? ???? – ??? ?????? ?????????, ???????? ??? ? ???????? ?????, ??? ???????? ??????? ?????????? ???????????? ????. ????? ????????? ???????????????? ?? ???????????? ???????? ????? ????? «?????????», ?????????? ????????? ?????????? ? ???????????? ?????? ? ??????? ????. ???????? ???? ?????? ?????????????, ?????? ?????????? ????????? ? ????? ?????? ?????, ? ???????????? ??????? ????????? ????????? ??????? ??? ??????? ?????? ??????. ? ??????????? ????????-???????? https://prometall.shop/ ???????????? ???? ? ?????, ???????? ????????? ? ??????????????? ????????, ? ????? ???????????? ???? ??? ????: «?????», «???????», «????? PRO». ???????? ?????????? ?????? ???????? ????? – ?? ???????????????? ???????????? ?? ???????? ?? ?????? ? ????????? ??? ????, ????? ????? ? ??????????? ???? ????????? ? ????????.
?????????? ?????? ?????? — ??????? ???????????????
https://vxtube.net/@diegohamblin2?page=about
??????????? ????????? ??????? ??????? ????????? ?????????? ? ?????????????? ??????? ? ???????????? ??????????. ???????????? ???????? «????? ?????????» ?????????? ?????? ????????? ? ?????????????? ? ????????????????? ?????????? ??? ????? ?????: ????????????? ???????????, ??????, ???????? ????????? ??? ???????? ?????????. ?????????????? ????????????? ?????? ???????????? ????????????? ?????? ??????? ?????????? ?????????? ?? ??????? ????. ?? ????? https://anapa-transport.ru/ ????? ???????????? ? ???????? ? ???????? ???????? ??? ????????????? ???????, ??????? ??????????? ??????????????? ??????????? ? ???????? ???????? ?????.
?????? ?????? ???
?????? ??????
?????????? ?????????? ? ??????? ?????? ??????? ?? ?????
https://www.masercondosales.com/agents/lupebeard0580/
?????? ??????????? ?????? ????? ????????? – ??? ????????? ? ??? ??????? ??????????? ???????, ????? ?????? ?????, ?????? ????????, ?????? ??????, ?????? ???, ?????? ???????, ?????? ????? ???, ?????? ??? ? ????????? ???????. ??????, ?????-?????????, ?????????, ???????????, ??????????, ????????, ????????????, ???, ???, ?????????, ???????????, ?????? ? ??? 100+ ???????.
?????????? ?????????? ? ??????? ?????? ??????? ?? ?????
https://cocotua.com/author/maxwhitford625/
1win ???? ???? 1win ???????
?????????? ?????? — ??? ??????? ? ?????? ???????
https://flixwood.com/@edisonmoe00209?page=about
?????? ?????? ?????? ??????
????? ???????? ?????????? ?????? ??????, 100%
https://git.graveyard.sh/ttpfranklin653
??????OFC ??????? ??????????? ? ???????? ????????.????????, ?? GGPokerOK ??????? ????? ????, ?? ????????? ????? ?? ???????????. ??? ????? ??????? ??????? ?????? ????: atom ?????????? ???????
? ?????? ? ?? ????????, ??? ???????, ??????? ???????.
?????? ??? ????????????? ?????? ??????? ???????? ? ?????? ?? ??????? ???????.
?????????? ????????? ??????? ?????? — ????? ????
https://git.tablet.sh/demetraduval15
?????????? ?????????? ? ?????????? ?????? — ?????? ? ??????
https://gitea.kdlsvps.top/kara9681620107
??????? ?????? ???????. ?????????? ?????? ?????????? ??? ?????????? ????????. ? ????? ?????????? ????? ?????? ??????? ?????? ??? ??????????? ?? ???????. ??????? ??????? dolphins pearl Atom – ?????? ?????? ????????? novomatic™ ??????? atom
atom??????????? ???????? ? ??????? «?????? ? ???????» ?? ?????????? ?????????? ????????? ? ?.
???????????: ???????? ????????? ???????????? ?????????? ?????? ?? ????? ???????.??? ?????? ????? ????????? ???????.
?????????? ?????????? ?????? ?????? — ?????
https://hgngit.ipdz.me/wesleyv2400529/7509056/wiki/tamozhennoe-oformlenie-38D
????? ???????? ?????? ? ??? ?? ?????? ?? taixinasia.com/chpu-stanki-iz-kitaya/ ???????????? ? ??????? ???????? ??????? ? ???????? ??????????? ??????????? ?? ????????? ??????????????: ???????????? ?????????????? ??????, ???????? ??????, ???????? ????????? ??? ????? ??????? ? ???????????? ??? ??????? ??????????????. ????????????? ??????????? «??????? ???????» ? ????? ??? 20-?????? ?????? ???????????? ?????? ????????????? ?????? — ?? ??????? ??????? ??? ?????????? ???????????????? ?????? ?? ???????? ? ??????????????? ????? ? ???????????? ???????.
??????? ?????????? ????? ??????????? — ??????? ? 17 ?????? ??????, ???? ??????????? ?????? ??, ???????? ????? ???????????, ????????, ????????, ????????, ??????????? ? ????????? ????, ????????? ????????? ????????? ?????? ? ?????? ??????? ????????. ???? — ??????, ????????? ????????, ?. 30/15, ??. 413, ???????? ????????????? ?????? ? ??????????? ????????????. ??????? ???????? ??????????????, ?????????????????? ? ?????? ?????. ???????? ?????????? ?????, ??????? ?????? ? ???????? ????? ? 5–10 ?????: https://advokat-laptinskiy.ru/
????? ?????? ?????????? ?????? ??????, ????????? ????????
https://kurdishserie.com/@charlinedorrin?page=about
???? ??????????????? ????????????????? ???? ?? ?????? ?????????????? ???? ???! ????: ????? ??????? ???????? – https://pediascape.science/wiki/User:Tanja97104
???????? ????????, ????? ?? ???????? ?????? – ??????
????????? ????????? ????? ?? ???????? ?????????????? ?????? ?????????.
?????????? ????????? ??????? ?????? — 5 ?????
https://mobishorts.com/@shirleyelder8?page=about
?????????? ?????? — ??? ??????? ? ?????? ???????
https://page.yadeep.com/hershelful
????? ????? ???????? ??? ? ?????????? ???????????, «???????????????» ? ??????? — ??????? ????? ??? ????????? ? ???????????: ?????????, ????????????, ???????, ??????, ?????????, ????????? ? ??? ?? ??????, ??????? ????, ???????? ? ??????. ???????? — ??????????? ????????????? «???????-?????????» ? ????? «??? ????», ???????????? ? ??? ??????????????? ?? ????, ? ??????? ????? ???????? ???????? ?????????? ????????????. ????????? ?? https://www.svartk.ru/ — ?????? ??????? ???????, ??????? ?????????????? ? ???????? ????? ? ????????????? ?????????.
????? ????? ?????? ?????
?????????? ?????????? ??????????? ?????? — ??? ?????
https://qtforu.com/@mireyabarela79
?????? ????? ?????? ?????
?????? ???? ???? ? ??????
???????? ????????? ????????? ????? ??????????? ??? ??????? ??????-??????? ???????????? ??????????? ? ???????? ????????. ??????????? Platl.ru ???????????????? ?? ??????? ???????????? ?????? ?????????, ?????????? ???????????? ? ???????? ??????? ??? ????????? ????????. ? ???????? ???????????? ????? ??? Steam, App Store, Xbox, ?????????? ??????? ?????????, ? ????? ???????? ??????????? ??????????? ??? ??????? ? ??????????. ????????? ?? https://platl.ru/, ????? ????? ?????? ??????? ?? ???????? ???? — ?? ??????????? ?? ???????-???????? ?? ?????????? ???????. ??? ?????? ???????????? ????????? ????? ?????? ? ??????????? ????.
????? ???????? ?????????? ?????? ??????, 100%
https://shuttershare.io/@marcus60663566?page=about
????? ???????? 300 000 ??????, ???? ??????? ?????????. atom casino, hotel ljubljana – ??????? ???????? ??????????? ???? atom
????????? ???? ???????? ?????????? ?????????, ???? ??? ?? ????????? ?? ?????????? ??????? ? ?? ??????????.
?????????? ???????? ??????? – 200 000 ?.
kasyno mostbet mostbet
?????????? ?????????? ??????????? ?????? ??? ????????
https://tiktok.dnacceler.com/@rochellmaygar?page=about
?????????? ???????? — ?????? ??????????? ?? ???? ??????. ?????? — ???????? ?? ?????????? ?????. ?????????????? ????? — ???????? ?? ???????? ??????? ??????. ???????????? ?????? — ?? ??????????. ???? ??????? ???????? ??????????? ???? – ??????????? ? Atom
???????? ??????????, ? ??????? ???????? ?????????? ?????????, ??????????? ? ???????.
???????????? ?? ???? ??????? ?????? ?? 1X222:45 25.03.2023???????? – ?????1.553.956.4 ????-?????: ??????-??????????, ???????, ??????????
At Rubbish Taxi, we manage your house clearance requirements, whether it is a home renovation, room redecoration, or clearing out old items. Our services cover comprehensive house removals and clearances across Dublin and other cities where we operate. We can collect various bulky items, including sofas, bed frames, mattresses, chest of drawers, wardrobes, fridges, freezers, washing machines, dishwashers, ovens, musical instruments, and more. Count on us for a seamless experience https://rubbish-taxi.ie/
?????????? ?????????? ?????? ?????? — ??? ?? ?????
https://worldclassdjs.com/edwinahyland53
????? ??? ??????? ?????????? ?????? ?????? — ??? ??????? ?? ????, ???????
https://www.e-vinil.ro/nikineighbour
????????-??????? https://mishiny.ru/ ?????????? ??????? ????? ????????, ???????? ??? ? ???????? ??? ??????????? ? ????????? ? ???????? ? ?????? ??????. ??????????? ???????? ????????? Michelin, Bridgestone, Continental, Nokian, Pirelli, Goodyear ? ?????? ????? ? ??????, ?????? ? ??????????? ??????????. ??????? ???????????? ??????? ?????? ?? ????? ?????????? ??? ???????, ? ????? ??????? ????? ? ???????????? ????? ????????? ??????????.
pixellaunch.click – Content reads clearly, helpful examples made concepts easy to grasp.
?????????? ?????????? ??????? ?????? — ????? ?????
https://www.vadio.com/@eugenio414048?page=about
????? ?????????? ?????? ? ?????? ? ?????????? ???????? ???????? ???? https://dvk-stroi.ru/ ??? ??? ????????? ??????? ?????? ????? ?? ??????? ? ??????? ??????. ?????????? ?? ????? ???? ????, ? ????? ?????? ???????? ????? ??????? ?? ?????????. ??? ????????????? ?????????? ???? ??????. ???????????? ???????? ???-????? – ??? ???????? ??????? ? ????????????? ??????? ???? ? ?????? ? 2007 ????!
??????? ???????? ??? ???????, ?????????? ?????????? ??????? ??????
https://dhivideo.com/@arnette3785192?page=about
???????? ????? ?????? ?????
oficjalne kasyno mostbet aplikacja mostbet na androida
?????? ???? ???? ?????? ??????
?? ???, ??? ???????, ???????? ??????? ? ??????????? ?????????, ??? ???????? ?? ???? ???. ???? ??????? ???????????? ??????? – ????????? ???? PlayFortuna ? ?????? – ??????? ??????? ???????? ???????????
???????? ?? ??, ??? ???? ?????????? ? ??????????? ????????????, ?? ????? ???????? ??????? ? ??????????? ???????? ???????????.
??? ????? ?????????? ?????? ?? ???? ????? ?? 100 ??????.
?????????? ?????????? ? ??????????? ?????? — ??? ????????
https://git.bluegrass.ipaas.io/aurorat8325117
Looking for minsk florist? Visit flower-shop.by and you’ll find only fresh roses and other flowers, as well as gifts, in our catalog. Our expert and experienced florists will create a stunning bouquet for any occasion. Purchasing fresh flower arrangements in Minsk to please your loved ones is simple! And our dependable flower delivery is available for you.
?????????? ?????????? ?????? ?????? — ????????? ??????
https://git.np-dms.work/fredrictrimble
?????? ?????? ????? ???? ?? ???????? ??? ?????????? ???? ???????. ???????? ?????? ? ?????? ???????????: ??????? ???????? ??????????? ???? Play Fortuna
?????? play fortuna?? ????? ????????? ?????????? ?????? ??????, ? ????? ????????? ????????????? ???????? ???.
???????? ?????????? ??????? ?????????, ??????? ???????? ???-?? ???????????, ??????? ???? ? ???, ??? ??? ?? ??????, ??? ???????????? ? ????????.
?????????? ???? ?????? — ?????????? ????
https://gitea.brmm.ovh/williemae44772
?????? ??? ????? ?p?????????? ??????? ????p????????: ???p??????? ? ????????????, c ????????? p??????? ? ?p????????, ???????????? ? ???????. ??????? ???????? ?????? ?????? ???? ??????? – https://reviews.wiki/index.php/User:NatishaHertzog7
???? ??????? playfortuna ???????? ??? ???:
? ??? ???? ???????, ??????? ???????? ??????? — «????????????? ?????».
?????????? ????????????? ?????? — ?????? ???????
https://gl.ignite-vision.com/kaitlynrodarte
?????????? ??????????? ?? ???, ?????? ??? ??????? ? ????? ???????? ????? ? ????????? ??????????? ?????, ??????? ? ??????????????????????? West-atlas.com ?????????? ?????????? ?????? ? ????????? ???????? ?????? ???? ?????? ???????, ????????? ?????? ? ???????? ????????? ??????????? ??????. ??????? ?????????, ???????? ?????????? ????? ????????? ? ?????? ??????? ? ??????? ?????? ???????????? ???????? ??????? ? ??????. ???????? https://west-atlas.com/ ? ???????????? ?????? ????? ????? ????????!
?????????? ?????????? ??????????? ?????? ??? ?????????
https://jovita.com/colinkent55118
??? ?????? ????? ??????? ??????????? ?????????? ??? ??????????? ?????????? ?????. ?? ??????????? ????????????, ????? ? ??, ??????? ???????????? ?????????. ????? ???????? ???????? ???????? ??????. ?????? ??????? ???????? ? ??????? ? ????????????? ??????????: http://onestopclean.kr/bbs/board.php?bo_table=free&wr_id=968742. ????? ????????? ?????? ???????????? ??????? ? ???????? ?? ????????.
?????????? ?????????? ?????? ?????? — ??????? ??????, ??? ??
https://makaan24.com/author/maurineimler0/
?????????? ????? ???????????? ?????? ??????????? ???????? ??????, ???????? ???????????? ??????????? ? ?????? ??? ?? ????? ???????? ???. ?????? Audiomap.ru ?????? ?????? ?????????? ????????? ????????? ?????? — ?? ?????????????? ??????? ?? ?????????? ? ????????????????. ??????? ????????? ?? ????????? ???????? ?????? ????? ???????????? ?? ????: ???????? ??????, ?????, ?????????????? ?????????? ??? ??????????????? ??????????. ???????? ?? https://audiomap.ru/ ? ????????? ?????????? ?????????? ????? ?????? ??? ??????????? ? ?????????? — ?????????? ??????? ???????????? ? ?????? ?????? ??????????????? ? ????????.
??????????? ???????????? ??????????? ????????? ????????? ??????????????? ?? ???????? ???????. ??? ????? ??????????, ??????? ?????????????? ? ????????????, ??????????? ???????? ?????????. ??? ???????????? ?????????? ? ???????? ?????????. ??????? ???????? ????????? ??????? ??????? ??? ????????? ????????????, http://storemango.com/bbs/board.php?bo_table=free&wr_id=3435290. ???????????? ?????? ????????? ??????????????? ?? ???????? ???????, ??????????? ?????? ???????? ? ????????.
?????????? ?????????? ??????????? ?????? — ??? ???????? ?? ???????
https://nigeria-real-estate.com/author/jolenehartwick/
???????????????? ???????? https://mebelniy-shchity.ru/ ????????????? ????????? ???? ?? ????, ?????, ???????????, ????? ? ???, ? ????? ??????????, ??????????? ?? ???????, ?????????? ??????? ? ???????? ?? ?????????????? ????????. ? ???????????? ???????????? ????????? ? ??????????????? ???? ? ????? ? ??????? ???????, ??????????, ????? ? ???-??????, ??????? ???????????? ?? ??????????? ???????????? ?? ????????????? ?????. ??????????? ???????? ? ?????????? ? ??????????????? ????? ????????? ??????.
??????????? ?????????? ??????????? ???????? ??????????????, ???????? ??????????, ???????????? ? ???????? ????????????. ??????????? ???????????? ???????? ???????? ?? ???? ??????. ???????? ???????? ??????? ??????? ??? ????????????? ??????? ??????????? ????????????. ????? ?????? ???????? ??? ????????? ? ??????? ????????, https://www.ebersbach.org/index.php?title=User:KerriMeece59. ??????? ?????? ???????? ?????????.
?????????? ?????????? ? ??????? ?????? — ?????? ? ?????
https://propdukaan.in/author/selinasimcox77/
????? ??????????? ??????? ?? ???????? ??????? ???????? agsvv.ru ???????????????? ?? ???????????? ? ??????? ??????????? ??????? ?????? «??????», ????????? ??????? ? ????????? ???????? ???????? ?? ???????????? ? ?????? ?????????. ? ???????????? ???????????? ???????????????? ???????? ??? ????? ????? ?????????????, ???????????????? ?????????? ??? ??????? ?????? ???????????, ????????????? ????????????? ? ????????????????? ??????. ??????? ???????? ???????? ???? ??? ?????????????? ???????, ?????????? ???????? ?? ???? ?????? ? ??????????? ????????? ?????????????.
??????? ?????? ?????? — ?????? ???? ? ?????
https://sakandar.com/author/valenciahaight/
??????? ???????? ?? ??????? 2025 ??????? ????????
rejestracja w mostbet mostbet android
??????? ???????? 2025 ??????? ???????? ?????????
?????????? ?????????? ?????? ?????? — ??? ??? ????, ?????? ?? ?????
https://suratvrproperties.com/author/vetarobles8438/
?????????? ?????????? ?????? ?????? — ?????
https://urlllll.com/crystlelockard
??????????? ???????, ?????????? ??? ??????? ????????? ? ??????, ????? ?? ????? ????????? ????????? ??????? ???????????????? ????????? ?? ??????? ???????? https://booking90.ru/ ???????? ?????????? ?? ??????????? ?????????? ??????????, ???????????, ??????? ? ???-??????? ??? ????? ?????? ? ??????. ??????? ????? ?? ???? ??????????, ??????????? ????????????? ? ??????????? ??????, ????? ?? ???????? ???????? ??????? ??? ??? ?????? ?????? ? ??????????????, ? ????? ??????? ????????? ??? ????????.
????? ?????? ????? ?????? ???????? ???????? ?????? ?????? ?? ??????, ???????? ? ?? ????? ???? ? ??? – sendflowers.by – ???? ? ???????? ?? ??????? ?????? ????? ?????? ????, ?????? ????? ? ??????? ??? ?????? ?????? ? ??????, ?????????????. ????? ?????? ?? ????? ????? ???? — ??? ????? ?????????? ??????? ? ???????, ? ???? ??????? ???????? ?????? ? ????? ???????. ???????????? ? ????????? – ??? ???????????? ????? ? ???????? ???????-??????. ????????? ?? ??????? ??????? ??? ????????? ?????????? ????.
?????????? ?????? — ??? ?????? ? ????????
https://wishi-washi.com/author/vtffernando843/
?????????? ?????????? ?????? ?????? — ??????? ??????, ??? ??
https://www.panjabi.in/@edwinvonwiller?page=about
???? ?? ?????, ???? ???? ? ????????? ??????. ?????? Eldorado – ??????????? ???? – ???????????, ???? http://dhi.org.mx/wiki/index.php?title=Usuario:DarrelFredrickse
????? ???????????? ??????????? ? ???????? — ???????????? ????, ??? ?????? ????????????? ??? ????????????? ?????? ?????? ? ??????? ? ?????????? ????? ??? ????? ?????????.
?????? ??? ????????? ??????????? — ??? ?????? ??????, ??????? ???????? ??????????? ??????? ???????????? ???????.
?????????? ?????????? ??????? ?????? ???????? ?? 2 ???
https://cutli.to/ofeliagillis6
??????????, ??? ????????? ???? ?? ?????????? ??????, ?? ?? ??????????? ?? ??????? ???????. ????????? ??????????? ? 1 ???? ? Eldorado ???? ? ?????????? – ?????? ?? ????? – https://wiki-staging.jgtitleco.com/index.php?title=User:FredrickToombs
?????????? ?????? ???????????????? ?????? ??? ??????????? ???????? ????? ??? ???????? ????? ??????, ?? ??? ?????????? ?????????? ???????? ????????? ????? ?? ?? ??????.
????? ????????? ?? ????????? ?? ?-????, ????? ? ??????? ???????? ?? ??????? «???????????».
?????????? ?????????? ???????????? ?????? — ??? ???????????????
https://g.6tm.es/sangsimmons396
?????????? ?????????? ??????????? ?????? ??? ????????
https://git.kirasparkle.de/leandrogsell31/7171904/wiki/tamozhennoe-oformlenie-27l
?????????? ??????????? ?? ????, ?????????? ?????????? ??????????? ??????
https://git.ultra.pub/eloisajenkin2/6825510/wiki/tamozhennoe-oformlenie+35b.-
??????? ???????????? ??????? ???????????? ????????????? ? ???????. ?????????? ?????? ??????????? ????, ??????????? ? ????, ??????, ??????: ??????? ??????? ????? ??????????
??????? ??? ????? ????? ?? ????? ????? ????? ??????????????????????? ????? ???.
????? ????????? ? ????? ???? ??????? ???? ??????, ??? ??????.
?????? ??????????? ??????? ?????? ?? ?????????? ????, ?? ???????????
https://gitea.quiztimes.nl/marjorieconawa
?????????? ??????????? ?? ????? ???????? ?????? ???? ?????: ??????????????, ??????, ???????????? ? ???????????? ?????????. ??? ???????????? ??????? ???????? ? ?????????? – https://de.wikisexguide.com/wiki/Diskussion:Petain_road. ??????? ???????? ? ????????, ??????? ???????? ?????? ? ??????????)
?????????? ?????????????? ?????? — ??? ?????? ? ????????
https://ibizabet.li/savannahmellor
?????? ?????? ??????? ???
?????? ?????? ??????? ???????
kraken market
kraken darknet
?????? ??????? ??????
vk1
????????????? ?????? ???????? ?? ??????? ?? ??????????? ???????? ???????????? — ?? ???? ??????????? ???????. ????????, ???????? ???? ? ????????????? ??? ?????????.
Latest about all things crypto: price rises and falls, network updates, listings, regulations, trend analysis, and industry insights. Follow market movements in real time.
The latest news crypto: Bitcoin, altcoins, NFTs, DeFi, blockchain developments, exchange reports, and new technologies. Fast, clear, and without unnecessary noise—everything that impacts the market.
?????????? ?????????? ?????? ????????
https://linkful.me/maureenhowitt3
?????? ???? https://opus2003.ru ? ?????? ????? ?? ?????????????: ??????? ????? ?????, ?????????? ???????, ????????? ????????? ? ??????? ???????? ?????????. ?? ?????????? ???? ??? ??????, ???????, ??????? ?????????? ? ????????????? ??????????.
kraken8
kraken2trfqodidvlh4aa337cpzfrhdlfldhve5nf7njhumwr7instad.onion
????? ????????????? ?????????? ???????? ???????? ???? sezon-podarkov.ru ? ?? ??????? ??????? ??????????? ????????? ?? ???????? ????? ? ??????? ?????????. ??????? ??? ??????? – ? ??? ??????????? ???????? ????? ????????? ? ???????????? ?????????? ??????? ? ??????-????????. ?????????? ?? ??? ??????? ??????. ????? ????????? ?????????? ?? ????? ????? ????????!
kraken ???????
?????? ?????
?????? ???? ??????
?????? ??????
?????????? ?????????? ? ??????????? ?????? — ?????
https://musiccosign.com/christoperprof
2krn
?????? ???????
??? 2. ????? ? ????????? ?????? «??????????». joycasino casino ???????? ??????? Joycasino
?? ??????????? ???? 12 ???? 2021 ? ?? ??? ??? ?? ????????? ??????.
???????, ????? ????? ?????????? ???? ????????? ? ???? ??????????? ?????????? ? ????????????? ?????? ?? ?????.
?????? ?????? ??????? ???????
?????? ???? ??????
???????? https://woodshop.group/ ???????????????? ?? ???????????? ?????????? ???????, ????????, ????????? ? ???????????? ?? ?????????????? ???????? ?? ????, ?????, ???????????, ????? ? ???. ???????????? ?????????????? ?? ??????????? ???????????? ? ??????????? ??????????????? ? ????????? ??????? ?? ???????, ??? ???????????? ?????????? ? ?????????? ???? ?????? ?????????. ??????????? ????????????? ? 2000 ???? ? ????????????? ???????????? ????????, ????????????????? ?????????? ??????, ???????????? ???????? ??????? ????????? ? ????????? ????????????? ?????????.
?????????? ??????? ?????? ?????? ????????, ??????? ???????
https://play.rueez.com/@reinaldovangui?page=about
kraken ??????
kraken ???????
????????? ?????????? ??????????? ?????? ?????? ?? ??????????? ????????? ? ??????????? ??????????, ???????? ??????????? ???????? ?????????, ??????? ?????????? ????? ?????????. ?? ????? https://mstroganov.ru/ ????? ????????????? ? ??????????? ?????? ?? ???????, ??????? ? ?????????????????? ?????????? ??????????, ????????????? ??? ??????????? ????? ? ????????? ???????????. ?????????????? ?????? ? ???????, ?????????????? ? ??????????? ? ?????????? ???????? ???????????? ?????????? ?????? ??????? ? ?????????????? ???-??????, ?????????? ???????? ?????????.
kraken market
Krn
????? ?? ????? ?????? ????? ?? ????? ???????
????? ?? ????? ???? https://narkonet.su
???? ?????????? ??????????? ??????????? ??? ???????????????, ??????? ????????? ????????? ??????????????????? ??????? ??????????????? ?? ?????? IP-?????. ????????? ???????????? ??????? ?????? ?????????, ??????? ?????? ? ?????????? RTSP, ??? ?????? ?? ????????????? ???????? ??? ????????? ?????. ????????? ???????? VMS (??????? ?????????? ?????), ??????? ???????????? ?????? ? ????? ???????????????, ? ????? ???????????????? ?????????? ? ??????????. ????????? ????????????? ????????? ???????? ??????? ????????????? ??? ? ????????????? ??????? ???????????, ??? ??????????? ???????? ?? ????????????? ? ??????????? ????????????. ????????????? ??????????? ??????????? ???????????? ???????? ????????, ??????????? ???? ? ????, ??? ?????? ??? ???????? ??? ?????????????? ???????????? ????????. ????????? ?????? ???????? ??????, ?????????? ???????? ? ????????? ???????, ???????????? ?????????? ? ???????? ??????? ? ???????. ?????????? AI-????????? ????????? ???????????????? ???????? ??????????? ? ???????? ????????????? ?????? ???????. ??????????????? ??????
?????????? ?????????? ??????? ?????? ?????? ? ??? ??????
https://redirectminia.site/iztemery460371
??????? ?????? ? ???????? ???????????? ?????? ? ????? ???????? ?????? ??? ??????? ?????????? ??????? ???????????, ? ?????? ?? ???? ?????? ???? ?????? ?????? https://store-drinks.com/. ????????? ??????????? ???????? ?? ????????????? ???????, ?????? ??????????? ??????? ? ?????????????????????? ???????: ????? ????????? ?? ?????? ??????? ? ?????????, ?? ? ????????? ?????????????. ??????? ?????? ?????? ?? ???????????? ?????????, ??????? ??????????? ???????? ? ??????? ?????????? ????????????, ??? ???????? ????? ??, ??? ?????? ??????????? ????? ??? ?????? ??????.
?????????? ?????????? ??????????? ?????? ?????? ? ??? ????????
https://soponetech.com/author/makaylamadrid/
???????? ???????? lev, ?? ??????? ???????????? ? ??? ????????? ? ?????????. ??? ???? ??????????? ?? ??? ????? ??????????? ???????? — ? ???????????, ??? Lev, ??? ? ??????. ?????? – ????????? ??????, ?????????? ??????????????, ??? ??????? ?? ??? 1 ???????. ???????, ????? ???? ? ??? ???? ??????? — ?????? ? 2014 ???? ?????????? ?????? ??????? ?? ??????-??????????. ??? ?? ????? ?????? ??????, ? ? ?????? ?????? ???????? ????? ?????????? ?????????? ?? ??? ???????? ???? ? ??????. ?????? – ????????? ??????, ?????????? ??????????????, ??? ??????? ?? ??? 1 ???????. ?????? ?????? ??? ? ??????? 2021 lev ??????????? ??????
?????? ? ??? ?????? ? ?????????? ?????? ?? ????????? ??????, ? ???? ??????? ?? ??? ?? ???????, ??? ?????? ??? ????? ?????, ?????? ???-?? ????? ??? ?????????? ? ???.
???????? ??????????? ?? ???????? ?????? ????? ????? ????????????? ??????? ??????.
????? ?? ????? ??????? ????? ?? ????? ??????
?????????? ?????????????? ?????? ??? ??????, ?????? ??? ??? ??????
https://trbs.link/monah596247590
???? ????????? ????????? ????? ? ?????????? ?? ??????????? ?????: lev ?????? – ??????????? ???? ????? ????? ? ?????? ?????? https://elearnportal.science/wiki/User:JulietHolte
??? ??? ??????? ??????????? ? ??????????, ???? ????? ???????? ???? ?? ???, ?????? ? ??????? ?????? ????? ?????????, ??? ? ??????????? ???????? ????????.
?? ??????? ?????????? ???.
???????? https://brusdoskamsk.ru/ ????????? ????????????? ???????????? ???????????? ? ???????????????????? ?????????? ?? ?????? ?????? — ?? ???????? ????? ? ????? ?? ???????, ????????? ????? ? ??????? ???????????. ??????????? ????????????? ? 1999 ????, ?????????? ????? 1500 ?????????? ??????? ?????????? ?? ???????? ???????????? ? ????????? ???????? ?????: ????????? ?????, ?????????, ?????????, ??????????? ???????? ? ???????????. ??????????? ???????? ???????????? ???????? ?? ?????? ? ??????? ? ?????????? ????????? ?? ??????.
Speel in het beste online casino zonder registratie Spin Panda Casino Nederland https://spinpandaa.nl/nl-nl en ontvang zeker een mooie welkomstbonus en gratis spins van ons. Vul uw rekeningen aan en neem geld op op elke handige manier. Meer dan 8.000 spellen – slots, videoslots, live casino’s, blackjack, roulette van toonaangevende aanbieders.
?????????? ?????????? ?????? ?????? — ??????? ?????? ??????
https://villago.homes/author/josephinebynum/
?????????? ??????? ?????? ?????? ?? ??????
https://www.italia24.tv/tube/@milla02i98870?page=about
kraken tor
Krn
?????? ??????
?????? ????
?????? ??????
kraken tor
kraken ???????????
?????? ?????? ??????? ???????
?????????? ?????? ??? ??????? ????????
https://zarnecka.com/marylinminnis
??????
kraken ??????
?????? ?????????? ??????
?????? ???????
Looking for secure cryptocurrency trading? Visit https://ff-io.to/ – a FixedFloat exchange with absolute security. We offer cutting-edge fixed-float swap technology, no registration barriers, and enterprise-grade security protocols. Learn more on the website.
kraken darknet
kraken ????
?????????? ??????? ?????? ?????? ?????? ?????
https://ferninnholidays.com/agent/sofiaharvill9/
?????? ?????
?????? ?????????? ??????
??????????? ?????? ??????
kraken ???????
?????????? ??????? ?????? ?????? ????????, ??????? ???????
https://git.daoyoucloud.com/hanneloreboehm
kraken ???????
??????
?????? ?????? ???
Krn
kraken ??????
kraken ??????
???????? ?????? https://china-star.ru ?? ????? ??? ????: ????, ????, ???? ? ??. ????????????, ???????? ??????, ??????????, ??????????? ? ?????? ???????? ???????????????. ??????, ??????? ? ?? ?????????? ?????????.
?????????? ?????????? ??????????? ?????? — ??? ????????
https://git.solidityteam.ir/audryolivarez
?????? ???? ??????
kraken ????
??????
kraken
kraken2trfqodidvlh4aa337cpzfrhdlfldhve5nf7njhumwr7instad
kraken tor
?????? ??????? ??????
?????? ?????? ???
?????????? ?????????? ??????????? ?????? — ??? ????????
https://gitea.isolaatti.com/florrader7901
kraken2trfqodidvlh4aa337cpzfrhdlfldhve5nf7njhumwr7instad.onion
kraken ???????
kraken market
?????? ?????? ??????? ???
??????? (???????????) — ???? ?? ???????? ??????????? ?????????? ??? ??????? ????????????-????????????? ???? ?????????????? ??????, ????????????? ???????? ???????????? ???????????? ?????????????? ? ?????????????? ?????????? ????????????. ?? ????? https://indenza.com.ru/ ???????? ??????? ???????? ????????, ?????????, ????????? 40 ? 160 ??, ? ????? ?????????? ?????????? ????? ???????????? ? ???????? ????? ??????. ????????? ? ?????? ???????? ???????????? ?????????, ??? ???????? ????????? ?????????? ??????? ? ??????????? ?????????????? ????????? ???????.
kraken ??????
?????? ??????
????? ???????? ????????, ? ????? ??? ??? ??????? ? ???????????? ????????????? ??????? ???????? ???? https://aglant.shop/ ? ?? ??????? ??????? ??????? ?? ???????? ??????, ??????? ???????? ???????? ??????????? ???????? ???????? ?? ??????? ??????????, ????????? ? ??????????? ??????????????, ? ??????? ????????? ? ????????? ?? ???? ??????. ????????? ?? ?????.
?????? ????
?????? ??????
Torentino — ??? ???????? ??? ???, ??? ????? ???????????? ? ????????: ?? https://torentino.org/ ??????? ???????? ????????? ??? ??? ?? ?? ????? ???? — ?? ?????????? ??????? ? ????? ?? ??????????? ????????, ????????? ? ????-????????. ??????? ????????? ?????????????? ?? ??????, ???? ??????? ??? ?????? ??????????? ? ???????? ?? ?????????, ??? ??? ????? ???? ??????? ????? ?????? ??? ?? ?????? ???????? ?? ???????? ?????. ?????????? ?????????? ? ??????????? ????????? ???????? ????? ? ???????? ????? ?????????? ? ???????? ????????.
?????????? ?????????? ?????? ?????? — ??? ?? ?????
https://heartbreakers.site/@donte64z993223
??? ????? ?? ??????
?????? ?????? ???
???????? ?????? https://lchina.ru ?? ????? ? ?????? ??? ????: ????, ????, ??. ??????? ?????? ?????????, ???????????, ?????? ? ???????? ? ???????????. ???????? ? ?????? ???????? ? ?????????????, ????????? ????? ? ??????? ????.
?????? ?? ??????
kraken ????
?????????? «??????» https://gastrodachavselug1.ru ?????????? ???????? ? ????????? ?? ????? ? ?????? ? ???????????. ??????????? ????, ??????, ????, ???????? ????? ? ???????? ????????? ????? ? ?????. ???????? ?????? ? ???????? ???? ??????? ??? ?????? ??????.
?????????? ?????????? ?????? ????????
https://kingdomshiftmedia.com/@reginaldtic164?page=about
?????? ?????? ??????? ???
?????? ??????????? ????
vk1
?????? ??????
? ????? ????????????? ????? ?????? ?????????? ??????, ??? ???????? ? ?????????? ????? ?? ?????? ?????, ? ???????? ?????????? ????????? ? ??????. ?????? http://storedrinks.com/ ???????? ??? ?????? DELIVERY DRINKS DUBAI, ????????? ?????? ????? ??????? ? WhatsApp, ???????? ??? ?????????? ???????. ??????? ???????? ?????? ? ????????? ??????????? ??????? ????????, ??????? ???????? ? ????????????????? ????????????. ??????? ????? ?? ???? ?????? ? ????????????? ? ??????????, ????? ?????????? ??? ??????????????? ?? ?????? ????? ? ????????, ?? ?????????? ? ?????????????.
?????? ?????? ??????? ???????
?????? ???
?????????? ?????????? ?????? — ?????? ????????????? ??????
https://michigancountryrealestate.com/agents/blondellcallah/
????????-??????? https://cybergarden.pro/ ?????????? ??????? ????? ?????????????? ? FPV-?????? ?? ??????? ??????????????, ??????? ???????????????? ?????? DJI Mavic 3, Matrice ? Agras ??? ?????? ? ????????? ?????????. ? ???????????? ???????????? ?????-???????????, ?????? ??? FPV, ???????? ???????????? ? ???????? ?????????? ? ???????????? ??????? ????????. ??????????? ????????????? ?????????? ???????????? ?????????????, ????????? ????????? ?? ???????? ? ??????? ??????????????? ??????? ? ????????? ???????.
kraken market
kraken market
????????? ?? ????? https://asiafast.ru ??? ???????? ????: ???????? ?????? ?????, ???? ? ??, ???????????? ?? ??????, ????????????, ??????????, ?????????? ??????????. ?????????? ???????? ?????? ? ??????????? ??????????? ?????? ??????.
?????? ?????? ???
vk1
??????????? ???????? https://gpcdoerfer1.com ? ??????: ?????????? ??????, ????????? ???????????, ????- ? ?????????????, ???????? ???????? ? ????????. ???????? ??????????, ????????????? ????????? ????? ? ???????????? ???????? ?? ?????? ?????.
?????? ?? ????? — ?????????? ?????????? ?????? ?????? ??? ????????
https://onedance.tv/@egbnatalia5819?page=about
kraken2trfqodidvlh4aa337cpzfrhdlfldhve5nf7njhumwr7instad
?????? ?? ??????
?????????? ????????? ??????? ?????? — ?????
https://qdate.ru/@celesteellswor
?????????? ????? ?????? ????? ?????????? ?? ????????
https://shamrick.us/beatriz48i147/beatriz1985/wiki/tamozhennoe-oformlenie-33U
???? ??????????? ???????, ??? ? ??????, ?????????? ???? ??????
https://testedwebsite.us/realestatee/agent/laynemccurry71/
??????-????? https://gvrest.ru ?????????? «??????»: ???????? ?????? ?????????? ???????? ? ????????? ?? ?????? ? ???????????. ????, ??????, ????, ????? ? ???????? ?????????? ??? ?????? ???????. ??????? ?????, ??????? ???????? ? ???? ????????? ???????.
???????? ?????? https://china-star.ru ?? ????? ??? ??????? ?????? ????????: ?? ????????? ?????? ?? ???????????. ??????????? ??????????? ???????, ??????? ?????????, ?????????? ? ??????? ???? ?? ?????. ??????? ????? ? ???????? ??????.
This is my first time pay a visit at here and i am actually impressed to read all at one place.
register in catalog Rio
?????????? ?????????? ??????????? ?????? — ??? ?????
https://vgreal.estate/author/bebe21s9494918/
?????????? ?????? ?????? — ??? ?? ?????? ??????
https://www.buyasiaproperty.com/author/whitneym083529/
Today’s Focus: https://parusbag.ru/forums/topic/verificzirovannyj-biznes-menedzher-fejsbuk/
The best of the best: https://beautyclinic.pe/buying-and-selling-tiktok-accounts-what-you-need-4/
????????-??????? https://cybergarden.pro/ ?????????? ??????? ????? ?????????????? ? FPV-?????? ?? ??????? ??????????????, ??????? ???????????????? ?????? DJI Mavic 3, Matrice ? Agras ??? ?????? ? ????????? ?????????. ??????? ???????? ???????????????? ?????? ??????????, FPV-??????, ?????????????? ??????? ? ???????? ???????????? ? ?????? ????????????? ???????. ???????? ???????????? ???????????????? ???????????? ????????????, ??????????? ???????????? ? ??????????? ???????? ?? ??????.
?????????? ????????????? ?????? ?? ???? ???? ?????
https://www.safeproperties.com.tr/agents/joannagreenlee/
?????????? ?????? ?????? ?????? ?????? ? ???, ?????????
https://dermerprection.xyz/williamsbromha
??????? ????? ????????? ???? ?????? ???????? — ??? ????? ????? ? ???????????? ??? ???????, ??????? ? ???????? ????????. ????????????? ?????? https://vip-pattaya.ru/ ?????????? ????????? ?????????? ?????????: ?? ???????? ???????? ? ???? ???? ?? ????????? ????? ?? ????????, «???????? ?????????????» ? ????????????? ?????????. ????????? ?????????, ?????????? ?????, ????????????? ????????? ? ??????????? ????????????? ??????? ?????? ??????????? ?????????? ? ??????????, ? ??????????? — ??????????? ? ??-?????????? ?????????????.
?????????? ?????????? ???????????? ?????? — ????????? ????????
https://git.advarna.fr/unasons3968513/una1984/wiki/tamozhennoe-oformlenie+77U.-
?????????? ?????????? ? ??????? ?????? — ??? ?????
https://git.manabai.net/randitulloch01
?????? ??????????? ??????? ?????? — 10 ?? 10
https://git.zguiy.com/cortezstonehou
? ?????, ????? ??????? ????? ???? ???????? ? ???????, ??????? SeoOm ?????????? ?? ?????? ??????, ? ??????????? ????????? ????????? ?????. ?? ????? https://seoom.ru/ ???????? ??????? ???????????: SEO ? SMM-???????????, ???????? ?????? ? ????????-?????????, ?????? ? ???????????? ? PR-??????????. ????????? ???????????????? ? ??? ????? ?? beauty-????? — ?? ???????? ???????? ?? ?????? ? ???????, ?????????? ????????? ????? ?????? ??? «?????» ???????, ? ?????????? ?????????? ? ????????? ????????? ?????????????.
?????????? ?????????????? ?????? ??? ??????, ?????? ??? ??? ??????
https://gitea.yanghaoran.space/jacksonried526/2954511/wiki/tamozhennoe-oformlenie-98e
????? ?????? ????? ??????, ? ?? ???????? ??? ??????, ??????-????? ?????????? ????????? ????????? ??? ???, ??? ????? ????? ? ????????. ?????? «?????-??» ?? ????? https://xn—-7sbujpz2a7c.xn--p1ai/ ?????????? ??????? ??????? ?????????? ????????: ?????? ??????????????? ?? 2–3 ??????, ??? ?????????? ?????????? ???????? ? ?????, ? ?????? ????????? ?? ????? ? ??????? 15 ?????. ????????? ???????? ?????????????, ???????????? ? ???????? ??? ?????? ? ???????????? ?????????? ??????? ??? ??????? ????????, ???????? ???????? ?? 1000 ?? 30000 ?????? ????????????, ??? ??????? ? ???? ? ??????????? ????????.
?????????? ?????????? ?????? ?????? — ??????? ??????, ??? ??
https://irania.tv/@alonzoy5731469?page=about
????? ????? ??????? ??? ?????????? ???????? ?????? t.me/kupitspravku ?????????? ??????? ? ???????????????? ????? ??????????? ??????? ??? ?????? ?????????? ? ?????? ??????? ? ????????. ????????? ???????? ??????????, ??? ???? ??????? ? ?????????? ? ??? ????????? ?? ????????, ? ??????? ????? Telegram ???????? ???????? ?????? ? ???????? ???????? ???????????. ???????? ????? ????? ?????? ?????????? ?? ?????????, ?????? ? ??????? ??????????, ??????? ????? ???????? ??????????? ???? ??????. ???????? ?????? ???????? ????????????? ??? ???, ??? ???????? ????? ? ???????????? ?????? ?????????????? ??????? ???????????? ? ???????????????.
?????????? ?????????? ? ??????????? ?????? — ??? ????????
https://luxury.homepro.casa/en/author/numbershallman/
????????-??????? https://mishiny.ru/ ?????????? ??????? ????? ????????, ???????? ??? ? ???????? ??? ??????????? ? ????????? ? ???????? ? ?????? ??????. ??????????? ???????? ????????? Michelin, Bridgestone, Continental, Nokian, Pirelli, Goodyear ? ?????? ????? ? ??????, ?????? ? ??????????? ??????????. ??????? ???????????? ??????? ?????? ?? ????? ?????????? ??? ???????, ? ????? ??????? ????? ? ???????????? ????? ????????? ??????????.
??????????? ??????????? ???????????, ?????????? ?????????? ??????????? ??????
https://mylinku.com/dominikwak
?????????? ????????????? ?????? ?? ??????, ????????? ?? ?????
https://prajna.cc/@heribertomccra?page=about
Greetings I am so thrilled I found your blog, I really found you by error, while I was researching on Bing for something else, Anyhow I am here now and would just like to say cheers for a remarkable post and a all round exciting blog (I also love the theme/design), I don’t have time to read it all at the moment but I have bookmarked it and also added in your RSS feeds, so when I have time I will be back to read a lot more, Please do keep up the awesome jo.
https://big-ip-client.com/
????????? ??? ?????? https://skillstaff.ru ? ???????? ?????????????, ?? ? ????????????: ???????????, ?????? ? ????????? ????????? ??? ?????? ????? ????????. ?????? ? ????????? ????????? ??????? ??????? ??? ??????????? ????? ? ?????????? ?????.
??????? ??????????? https://proctofor.ru ? ?????? ? ??????????? ????????????? ? ???????? ???????. ???????? ?????????? ??????????? ? ??????? ????????, ??????, ???????, ?????????????? ??????????? ?????? ?????. ????? ?? ??????, ??? ????????, ? ?????????? ????????. ???????? ??????, ??????? ??????, ??????????? ? ????????? ?????????.
?????????? ?????? ?????? ??? ???????? ????
https://rhoming.com/agent/thomasmcquade9/
Aw, this was a very good post. Taking a few minutes and actual effort to make a great article… but what can I say… I procrastinate a whole lot and never manage to get anything done.
openconnect
?????????? ?????????? ?????? ?????? — ??????? ??????, ??? ??
https://stephens.cc/porfiriolundbe
Wow, fantastic weblog structure! How lengthy have you been running a blog for? you made running a blog look easy. The entire look of your web site is excellent, as well as the content!
cisco secure client
Excellent blog you have here but I was curious if you knew of any user discussion forums that cover the same topics discussed in this article? I’d really love to be a part of community where I can get feedback from other experienced individuals that share the same interest. If you have any recommendations, please let me know. Kudos!
sonicwall netextender mac
?????????? ?????????? ?????? ?????? — ??? ????????
https://tv.thechristianmail.com/@ingeborgtyrrel?page=about
????????????? ????????????? ??????????? MetallProduct 61 ???????????????? ?? ?????????????? ??? ? ???????????? ??? ??????? ?? 10 ?? 5000 ?, ????????? ??????? ??? ???????? ??????????????, ???? ? ???????????? ?????????. ?? ????? https://metallproduct61.ru/ ???????? ??????? ??????????? ??????????????, ??????? ?????????? ? ????? ????? — ?? ?????????????? ?? ??????? «??? ????». ????????????? ????????????????? ??????????, ??????????? ?????????? ?????? ? ?????????????? ?????? ? ??????? ?????? ???????????? ?????????, ????????????? ? ?????????? ?????????? ?????????? ???? ? ??????? ???????? ????????????.
?????????? ?????????? ?????? ?????? — ????????? ?????????
https://webba.cz/@newtonwilks828?page=about
??????? ??? ???? https://kopkol.ru ? ?????????? ??????? — ???????, ?????? ? ???????????? ????????????? ? ?????????. ????????????? ??????? ? ???????? ??????? ????? ???????, ??? ???? — ?? ??????? ?? ????? ????. ???????? ? ???????? ???, ????????????? ??????, ???????? ? ???????? ????????????. ?????? ???? ?? ????? ??????? ??? ???????? ? ????????.
?????????? ????????? https://sever-geo.ru ? ?????? ? ?????????? ??????? ??? ????????????? ????? ?????, ?????????, ???????????? ? ???????????? ????????. ????????, ????????, ????????, ???????????? ??????? ? ?????????. ???????? ?? ?? ? ????, ???? ??? ? ??? ??????????? ????????????. ?????????? ??????????? ????? ??? ?????????????? ? ????????????. ????? ?? ?????? ? ???????? ?????, ?????????? ?????, ????????????? ?? ????? ???????.
?????????? ??????????? ?????? ????? — ??? ?????? ???????????, ??????? ?????????? ? ????????????????? ?????????? ?????????????? ? ?????? ?????????? ???????? ? 1995 ????. ?? ????? https://alexberg.site/ ???????? ??????? ?????? ?? ???????? ??????? ?????, ???????????? ??????????? ? ??????? ????????? ??????????, ??? ?????? ?????? ????????????? ??? ??????? ????????????? ??????????. ?????????????? ??????, ???????? ? ???????????????? ????????? ? «????????? ????????» ?? ???????? ????????? ?????????? ???????? ?? ????? ????????, ? ??????????? ?? ?????? ????? ??? ????? ? ??????.
?????????? ?????????? ???????????? ?????? — ????????? ????????
https://www.musicsound.ca/felipadesailll
?????????? ????????????? ?????? — ?????? ???????
https://code.sammer.vip/arnoldoostrand/8055619/wiki/tamozhennoe-oformlenie-28i
??????????? ???? ?????????? Sofokast Plus®, Velakast® ? Daclatasvir® ???????????? ?????????? ?????????? ? ??????? ???????????? ????????? ???????? ? ? ???????????? ? ???????????? ?????????????? ????????? ??. ?? https://sofokast.ru/ ???????????? ????? ???????, ?????????, ???????????? ??????, ? ????? ?????? ?? ????????????? ?????????? ??????????? ? ????????????? ? ?????????????. ?????? ???????????? ??? ?? ??????-?????????????? ? ???????????, ??? ? ?? ?????????, ??????? ???????? ??????????? ??????? ? ??????? ? ????????? ?? ?? ????? ??????? ?????? ?? ????? ????????????? ????????.
???????? ?????????? ??????? https://ng-logistic.ru ??? ???????????? ????????, ??????????????????, ?????????? ? ???????????? ????????. ???????? ??????? ?????? ????????, ?????????? ????? ? ??????? ?????????????? ??????? ?? ???????. ?????? ??????????? ??????????, ?????????? ???????? ? ???????? ?????????. ??????, ???????????? ????, ?????? ?????? — ??? ??????????? ?????? ? ?????????.
?????????? ?????? ?????? — ??? ?? ?????? ??????
https://forgejo.maledict.me/nidiamackay652
???????? ????? https://bio-grunt.ru ? ?????? ?? ?????? ? ?????????? ??????? ??? ???, ???????? ? ??????????? ?????. ??????????? ?????, ???? ??? ????????? ????????? ?????, ??????? ???????? ????? ??? ?????? ? ?????. ??????? ?????? ?????, ?????????? ????????, ?????? ? ??????? ??????. ???????? ? ???????? ?????? ? ?????????????, ????????????? ?????????. ???????? ????? ?? ??????? ??????????? ? ??????? ? ????????.
????????????? ????? https://????????.?? ??? ???? — ?? ?????????? ?? ???????? ???????. ??????????????, ????????????, ?????? ??????????, ?????????? ???????, ??????, ?????????? ???????????? ? ?????????? ??????. ???????? ?? ????????, ????????? ?????, ????????? ????? ? ??????????. ??????? ??????????? ??? ????? ????? ??? ??????? ? ?????????, ? ????????? ???????? ?? ??? ???????? ???? ?????.
??? ???, ??? ???????? ? ???????? ?????? ????????, ???????? ??????? ?? ???????????? ?????-???? ?????????? ???????? ?????????????????????. ?? ????? https://press-forma.by/ ???????? «???????????» ?????????? ?????? ????: ?????????? ? ???????????? ?????-????, ????? ???????, ?????? «??? ????» ? ??????? ??????? ???????. ??????????? ???????, ????????????????? ???????? ? ?????? ????? 10 ??? ? ????????????????? ?? ????????????? ????????????? ????????? ????????? ????????? ????? ? ??????????? ?????????????, ? ?????????? ?????? ????????? ???????? ????????? ??????????? ?????? ???????? ????????????.
?????????? ?????????? ?????? ?????? — ??? ????????
https://git.hubhoo.com/dianemolinari5/4263986/wiki/tamozhennoe-oformlenie+5u.-
????????? ??????????? ?????? ??????? ????? ?????????? ?? ??????? ????????????? ??? ?????? ?????????? ???????? ??? ???? ?? ???????????? ?? ??????? ? ??? ???????.
????????? ??????? ???????? ??????? ???????? ? ????
???????????????? ????????? https://stsgeo.ru ??? ????????????? ?????? ????? ? ??? ? ???????????????? ???????? ? ??????????. ????????? ??? ?????????? ?????????, ??????????? ???????? ?????, ?????? ????????????? ? ???????. ?????????? ??????????? ?????? ??????????, ??????????, ???????????, ??????????? ?????????.
?????? ?? ????? — ?????????? ?????????? ?????? ?????? ??? ????????
https://git.thomasgoossen.nl/sanfordbonwick
?????? ????????? ??????????? ??????? ?????? — ?????, ????????? ? ????
https://gitea.noname-studios.es/juliostedman7
???????, ??? ?? ??? ???????? ? ?????? ? ?? ????????? ???? ????????? ???????? ???? https://aivengogeo.com/ ??? ?? ????????? ??? ???? ??????! ??????? ??? ?? ?????????? ???????? ???????. ??? ???????? ?????? ?? – ? ???? ????, ???? ?? ????????. ??-?????????? ???????? ?? ??????? ? ????? ?????? — ?? B2B-????? ? ??????????? ?? e-commerce ? ?????????? ???????. ??????? ??????????????? ?????????????!
???????? ?????? https://avalon-transit.ru ?? ????? «??? ????» ??? ??????? ? ????????-?????????. ????-, ?/?-, ??????? ? ????-?????????, ???????????? ?? ???????, ???????? ??????, ???????????, ?????????? ? ???????? ?? ?????. ???????? ? ?????? ???????? — ?? ????????? ???????? ?? ???????????. ?????????? ?????????, ??????????, ?????? ? ?????????? ? ????????????? ?? ???? ?????? ????????? ?? ?????.
??????? ?? ???????????????? ?????????? ????????????? ??????
https://homeablazebyhispresence.dennmachinery.com/@nereidatreat1?page=about
?????????? ?????? ??? ??????? ????????
https://learnhub.greellc.com/@zita3305150238?page=about
???????????????? ???????? https://mebelniy-shchity.ru/ ????????????? ????????? ???? ?? ????, ?????, ???????????, ????? ? ???, ? ????? ??????????, ??????????? ?? ???????, ?????????? ??????? ? ???????? ?? ?????????????? ????????. ? ???????????? ???????????? ????????? ? ??????????????? ???? ? ????? ? ??????? ???????, ??????????, ????? ? ???-??????, ??????? ???????????? ?? ??????????? ???????????? ?? ????????????? ?????. ??????????? ???????? ? ?????????? ? ??????????????? ????? ????????? ??????.
????? ???????????? ??????? ????????????? ??????? ????????? ?????? ?????, ?? ???????? ???????????????? ?? ??????????? ?????? ?????????. ??????? ?????? ???? ??????? ?? ??????? ? ??: http://idrinkandibreakthings.com/index.php/User:JovitaIrons
????????? ?50 ??? ???? ??????? ?????, ???? ??? ????????? ???????, ??????? Aviator game ??? ????????? ????? ???????.
?????? ??????????? ????? ???? ????.
?????????? ?????? — ??? ?????? ? ????????
https://movie.actor/@elitomlin74197?page=about
?????????? ??????????? ?? ????, ?????????? ?????????? ??????????? ??????
https://perfectneighbourhood.com/author/vernstoner1479/
??????? ?????????????? «??????» ? ?????? ?????-?????????? ???????? ????????? ???????????? ?????????? ? ????????? ? ???????????? ????????? ????? ?? ??????? ??????. ?? ????? https://xn--80ac8agj0c.xn--p1ai/ ???????????? ?????? ?? ?????? ??????? ? ?????????? ?????? ?? ??????????? SPA-???????? ??? ???? ? ?????????? ??????? ? ????????????? ???????. ??????? ???????, ??????????? ??????, ?????? ?? ??????? ? ????????????, ?? ?????? ????????? ?????? ????? ?? ?????? ??????? ? ???????????, ? ????????? ????????, ????? ???????? ??????? ???????????? ?????.
?????????? ?????????? ? ??????? ?????? — ??? ?????
https://rayandco.uk/author/berniecewpa039/
????? ?????????? — ??????? ? ??????????? ????????? 17 ???, ???? ?? ??, ???????? ???????????? ???????????, ????????, ????????, ????????, ??????????? ? ????????? ?????, ????????? ???????? ????????? ? ???????? ????????? ?????. ????? ??????? ?? ????????? ?????????, ?. 30/15, ??. 413 ? ??????; ???????? ????????? ?????? ? ??????? ????????????. ?????????? ????? ??????????? ???????, ??????? ?????????????????? ? ?????????? ??????. ???????? ?????????? ?????, ??????? ?????? ? ???????? ????? ? 5–10 ?????: https://advokat-laptinskiy.ru/
??? ????? ?? ??????
?????? ??????
???????? ?????????? ?????? ??????, ???????? ?? ?????? ???
https://skiivie.com/@quintonmoseley?page=about
????????? ?? ?????: ??????-??????? ?????????
?????????? ?????????? ??????????? ?????? — ??? ?????
https://tippy-t.com/tanyacampos16
Today, while I was at work, my sister stole my iphone and tested to see if it can survive a twenty five foot drop, just so she can be a youtube sensation. My apple ipad is now destroyed and she has 83 views. I know this is totally off topic but I had to share it with someone!
wisenet viewer download
Right here is the right webpage for anyone who really wants to find out about this topic. You know a whole lot its almost hard to argue with you (not that I actually would want to…HaHa). You definitely put a fresh spin on a topic which has been written about for decades. Wonderful stuff, just wonderful!
admanager plus
???????? ???????? «??? ???» ? ???????? — ???????? ????????? ???????????? ? ??????????? ??? ???????????? ? ???, ?????????? ??? ? ?????????? ???????????, ??? ? ? ???????? ???????????. ?? ????? https://tkmoycar.ru/ ??????????? ??????? ???????: ?????????????? ???? ?????, ????????????? ? ??????????????? ????????????, ?????????? ? ??????????. ??????????? ???????? ?????? ? ???????, ????????, ???????????? ? ????????? ????????????, ??? ????????? ??????????? ??????????? ?????????????? ??????? «??? ????» ? ?????????????? ??????? ???????.
Excellent site you have here but I was curious if you knew of any discussion boards that cover the same topics discussed in this article? I’d really love to be a part of group where I can get feedback from other experienced people that share the same interest. If you have any suggestions, please let me know. Thanks a lot!
palo alto globalprotect download
?????????? ????????????? ?????? ?? ??????, ????????? ?? ?????
https://videoasis.com.br/@randi65n921280?page=about
https://towing.com.pl
I think everything said made a great deal of sense. However, think about this, what if you were to write a killer headline? I am not suggesting your information isn’t good., but what if you added a headline that makes people want more? I mean %BLOG_TITLE% is a little plain. You ought to glance at Yahoo’s home page and note how they create article headlines to grab viewers to open the links. You might add a video or a related picture or two to get readers excited about what you’ve got to say. Just my opinion, it might make your blog a little livelier.
citrix secure access download
I loved as much as you’ll receive carried out right here. The sketch is tasteful, your authored material stylish. nonetheless, you command get got an edginess over that you wish be delivering the following. unwell unquestionably come more formerly again since exactly the same nearly very often inside case you shield this hike.
watchguard ssl vpn download
???????????????? ?????????? ?????? ????? ?????? ?????? v3 ?????????? 56-?????????? ????? ??? ??? ?????????? ????? ??????? ??? ?????? ???????? ??? ?????????? ????? ???????????.
For the reason that the admin of this web page is working, no uncertainty very shortly it will be famous, due to its quality contents.
Qfinder Pro download
?????????? ?????????? ?? ??????????? ????? ??????? — ??? ?? ?????? ?????????, ? ?????? ????????? ?????? ?????????? ? ????? ????. ? ????????-???????? «???????» ?? ?????? https://www.florion.ru/catalog/novogodnie-kompozicii-iz-nobilisa ???????????? ????? ??????????? ?? ????????, ??????? ????? ?? ????????? ? ????????? ?????????? ??????? ??????. ???????? ??????????? ?????? ?????? — ?? ????????? ?????, ????? ? ?????? ?? ???????????? ???????? — ???, ????? ?????????? ????????? ????????? ? ???????? ? ????? ????? ??????? ???????????? ?????? ? ????????, ????? ??? ?? ?????????? ?????.
Strona internetowa mostbet – zaklady sportowe, zaklady e-sportowe i sloty na jednym koncie. Wygodna aplikacja mobilna, promocje i cashback dla aktywnych graczy oraz roznorodne metody wplat i wyplat.
?????????? ????????????? ?????? — ???????? ???????
https://www.happylove.it/@tresaweinman45
What’s up, its nice paragraph concerning media print, we all be aware of media is a impressive source of information.
fortinet vpn client
?????? ?????????? ????????????, ???????? ? ??????? ????? ????? ???????????? ?????????? ??? ??????????????, ? ???????? ?????????? ???????? ????????? ????? ???????? ??????????. ?? ???????? https://inpekmet.ru/lazernaia-gravirovka ???????? «?????» ???????????? ? ???????????? ???????????? ?????????? ?? ??????? ????? ????????? ? ????????? ????????????? ??????? ???????? ?? ??????. ??????? ?????????? ????????? ????? ??? ???????? ??? ?????????? ????????????, ????? ???????? ??????, ????????????? ??????? ? ???????????, ?????????? ? ???????, ??????????? ????? ? ???????????? ???????????? — ?????? ?????? ??? ????????????, ????????? ? ????????????.
?????????? ?????????? ? ?????????? ?????? — ?????? ? ??????
https://xajhuang.com:3100/judithmackinto
????????-??????????? ???? ??????? ???????????????? ?? ???????????????? ??????????? ? ??????? ? ?????? ? ???????? ??????. ????? ????????? ????????????? ? ??????? ?? ????? egorkosarev.ru ??????????? ?????? ?????? ?????: ?? ????????? ??????? ? ??????? ??????? ?? ????????????? ???????? ? ????????? ?????. ???????? ???????? ??????????? ???????? ?? ???? ?? ???????? ???????: ?????????????? ?????? ???????? ????????, ? ??????????? ??????? ?????? ??????? ?????????????? ??????.
???????????????-??????????? ???????? «????????-?????» ?? ????????????? ???????????????? ?? ??????????? ?????????? ???????? ??? ??????? ? ???????? ????? ?????????. ?? ????? http://express-svyaz.ru/ ???????????? ?????? ?? ??????? ? ???????????? ?????? ???????????????, ?????????, ???????-???????? ????????????, ???? ? ????????????, ? ????? ?????????????? ? ???????????? ??????????????????, ????????? ?????? ? ???????? ??????. ???????? ???????? «??? ????», ??????? ?????????? ?????????? ? ??????????? ????????????, ??? ????????? ?????????? ???????? ???????? ?????????????? ? ??????? ??????? ? ?????????? ????????.
Hi there everyone, it’s my first visit at this site, and post is actually fruitful in support of me, keep up posting these types of articles or reviews.
forticlient mac download
?????????? ????????????? ?????? — ?????? ???????
https://egarealtygroup.com/agents/dominiquegavin/
?????? ?????? ???????? ??????? ??????? ??? ???????? ??????????? ?? ????? iPhone ? ?????-??????????. ????????-??????? i4you ????? ?????????? ??? ???????, ??????? ???????????? ????? ????????????? ??????????. ? ????? ???????? ???????????? ???????? ????????? ???????????? ????????? Apple. ?????? ???????? ?????????????? ??????????? ????????? ????????????? ?????? ?? ???? ? ?????, ??? ???????????? ??? ??????????? ? ??????????.
https://abakan.ru/index.php/chto-proiskhodit/v-rossii/item/19694-chto-uchest-pri-vybore-tsvetov-sovety-dlya-zapominayushchegosya-podarka
?????? ??????????? ??????? ?????? ???? ?????? ??????
https://git.bpcspace.com/brianne72z658
?????? ?????? ?????????: https://medim-pro.ru/kupit-spravku-iz-psikhdispansera/
?????????? ?????????? ???????????? ?????? — ??? ???????????????
https://git.pgia.ru/duanewhitcomb4
?????????? ?????????? ?????? ?????? ??????? ?????? ??? ???????
https://gitea.chloefontenot.org/ivoryhobart28
??????? ??????????????? ????????? ????? ??-???????, ?? ????????? ????????? ???? ?????? ????????-??????????????? ????? ? ?????? ??????-???????? ? ?????????? ???????????. ????? J-center Studio ? ?????? ?? ????? https://j-center.ru/ ?????????? ????????? ??? ???????? ? ??????????? ????????: ?? ??????? ?????? ? ???? ?? ?????????? ??????????, ??????? ???????????? ? ?????????-???????????. ??????? ??????????, ???????? ????????? ?? ??????? ? ????????? ???? ????????? ?????? ???????????? ????????? ? ???????? ????? ?? ????? ?????-?????.
?????????? ?????????? ??????????? ?????? — ??? ?????
https://go.atamarii.com/@jarrodsouth729
?????????? ?????????? ?????? ?????? — ??????? ?????? ??????
https://karabass.pro/@shanicecoxen82?page=about
?????????? ??????????? ???????? https://medim-pro.ru ? ??????? ??? ???????? ? ?????? ??????????. ?????? ? ??????????????? ???????, ????????????? ?? ???? ??????, ?????? ? ???????????. ???????? ???? ????? ? ????????? ??????????????????.
???????????????? ???????? https://mebelniy-shchity.ru/ ????????????? ????????? ???? ?? ????, ?????, ???????????, ????? ? ???, ? ????? ??????????, ??????????? ?? ???????, ?????????? ??????? ? ???????? ?? ?????????????? ????????. ? ???????? ???????? ????????? ? ??????????????? ??????????? ? ?????? ? ??????? ???????, ???????????? ?????, ???????? ? ???-???????, ??????????? ?? ????? ????????? ????? ?? ???????? ??????????. ??????????? ???????? ? ?????????? ? ??????????????? ????? ????????? ??????.
?????? ???
?????? ?? ??????
????? ?????? ?????????? ?????? ??????, ????????? ????????
https://mbhomes.ae/author/petersprouse33/
????? ?????? ????? ?????? ? ??? ?????? ??????????, ?????? ??????? ??????-?????? «????-?????» ???????? ????? ?????????? ??????????? ?? ????????? ??????. ?? ????? https://zaym-agent.ru/ ?????? ?????????? ??????? ??? ?????? ? ????????? ?? ??, ??? ????? ???????? ???? ?? ????? ?????????????, ? ??????????? ??????? ?????????? ? ??????????? ?????????. ??????? ???????, ???????? ???????? ? ?????? ?? ??????????? ???????????? ????????? ????????????? ????????? ??????? ??????? ? ?????????? ?????????? ?, ??? ?????????????, ? ??????? ??????? ??? ????? ????????.
???????? https://woodshop.group/ ???????????????? ?? ???????????? ?????????? ???????, ????????, ????????? ? ???????????? ?? ?????????????? ???????? ?? ????, ?????, ???????????, ????? ? ???. ???????????? ??????? ?? ??????????? ????????? ? ?????????????? ??????????????? ? ????????? ????????? ?????, ??? ??????????? ????????? ? ????????????? ???????. ??????????? ????????????? ? 2000 ???? ? ????????????? ???????????? ????????, ????????????????? ?????????? ??????, ???????????? ???????? ??????? ????????? ? ????????? ????????????? ?????????.
https://demo-jet.jetwp.ir/blog/2025/10/25/melbet-vhod-registratsiya-2025/
?????????? ?????? ?????? — ??? ?? ?????? ??????
https://nonstopvn.net/@graigchaney22?page=about
https://pandaiqq.com/melbet-zerkalo-rabochee-2025/
https://dcrown-residence.com/melbet-bonus-za-registraciyu-2025/
https://jaya333.com/melbet-vhod-zerkalo-2025/
https://noorhotelukhiya.com/bonus-kod-melbet-2025-obzor/
https://smis.edu.mz/melbet-2025-obzor-bk/
https://www.tkaninovekompenzatory.cz/melbet-obzor-2025-bk-igroki/
?????????? ?????? ?????? — ??????? ???????????????
https://propertyguides.in/author/delia950087348/
https://rm-kinesiologue.ca/2025/10/25/melbet-obzor-2025-2/
https://www.faifai.tv/????۠???/754104/
https://queirozcirurgiaplastica.com.br/skachat-melbet-obzor-2025/
https://huntbconstruction.com/sayt-melbet-obzor-2025-stavki-bonusy/
?????????? ??????????? ?? ????, ?????????? ?????????? ??????????? ??????
https://sarahjoanthailand.com/author/tammybillups06/
https://www.weconsultit.tech/melbet-obzor-bk-2025/
https://www.netamagaza.com/melbet-obzor-2025-bk
https://www.jeykeyrugs.com/melbet-polnaya-versiya-sayta-2025-obzor/
https://intermodalsas.com/2025/10/25/skachat-melbet-2025-obzor/
?????????? ??????? ?????? — ??????, ?????, ????????
https://suvenduhomes.com/agent/georgianauju6/
?????????? ?????????????? ?????? ??? ?????? ??????
https://urlroxx.com/archerwentcher
???????????? ?????? ??? ???????, ??????? ?? ?????????? ?????????? ???????????? ??????
https://worship.com.ng/kirstenpratt17
?????? ??????????? ??????? ?????? — 10 ?? 10
https://www.prophecyhousing.com/author/clarissausg196/
??????? ?????? ?????? — ?????? ???? ? ?????
https://daftsex.lol/@bettiehardacre?page=about
???????? https://woodshop.group/ ???????????????? ?? ???????????? ?????????? ???????, ????????, ????????? ? ???????????? ?? ?????????????? ???????? ?? ????, ?????, ???????????, ????? ? ???. ???????????? ?????????????? ?? ??????????? ???????????? ? ??????????? ??????????????? ? ????????? ??????? ?? ???????, ??? ???????????? ?????????? ? ?????????? ???? ?????? ?????????. ??????????? ????????????? ? 2000 ???? ? ????????????? ???????????? ????????, ????????????????? ?????????? ??????, ???????????? ???????? ??????? ????????? ? ????????? ????????????? ?????????.
????????? ?????????? ??????????? ?????? ?????? ?? ??????????? ????????? ? ??????????? ??????????, ???????? ??????????? ???????? ?????????, ??????? ?????????? ????? ?????????. ?? ????? https://mstroganov.ru/ ????? ????????????? ? ??????????? ?????? ?? ???????, ??????? ? ?????????????????? ?????????? ??????????, ????????????? ??? ??????????? ????? ? ????????? ???????????. ?????????????? ?????? ? ???????, ?????????????? ? ??????????? ? ?????????? ???????? ???????????? ?????????? ?????? ??????? ? ?????????????? ???-??????, ?????????? ???????? ?????????.
?????????? ?????? ?????? ?????? ?????? ? ???, ?????????
https://ggapps.xyz/kayleighchowne
Telegram-????? ? ????????? – ????????, ????????? ?????????, ?????? ? ????? ?????? ??????
Dragon Money Studio
????-????? ???? ??? ??????? ????? ????, ????????????? Book of Dead ??? ????? ? ????? ????? ????????
?????? ???? ??????
?????? ??????? ??????????? ???? ? ?????, ????? ????? ???????
Dragon Money Studio
?????????? ?????? ?????????? ???????, ??? ???????
https://git.lmbrs.org/valoriemonroy4
I’d like to find out more? I’d love to find out some additional information.
fortinet vpn download
?????????? ?????????? ?????? ?????? ??? ????
https://git.wantbug.com/jacintodelgadi/7992673/wiki/tamozhennoe-oformlenie+76j.-
Free video chat Emerald Chat find people from all over the world in seconds. Anonymous, no registration or SMS required. A convenient alternative to Omegle: minimal settings, maximum live communication right in your browser, at home or on the go, without unnecessary ads.
?????????? ?????????? ?????? — ?????? ????????????? ??????
https://gitea.stormyhome.net/alena361912221
??????? ?? ???????????????? ?????????? ????????????? ??????
https://icefilm.ru//@kevinadams1060?page=about
?????? ?? ????? — ?????????? ?????????? ?????? ?????? ??? ????????
https://linksc.click/garland24x147
Its like you read my mind! You seem to know a lot about this, like you wrote the book in it or something. I think that you can do with some pics to drive the message home a bit, but instead of that, this is wonderful blog. An excellent read. I’ll definitely be back.
Qfinder Pro
?????????? ?????????? ?????? ?????? — ?????
https://my70size.com/@garnetfreeling?page=about
??????? ?????????? ?????????? ? ??????? ?????? — ?????? ? ??????
https://playindia.sanjitchaurasiya.com/@tashat56865201?page=about
Free video chat visit site find people from all over the world in seconds. Anonymous, no registration or SMS required. A convenient alternative to Omegle: minimal settings, maximum live communication right in your browser, at home or on the go, without unnecessary ads.
?????????? ?????????? ???????????? ?????? — ????????? ????????
https://reelx.uk/@janiceraines10?page=about
?????????? ?????????? ? ??????????? ?????? ?????? ?? ???
https://sounddeep.blacktube.in/xaviercarnahan
??????????????? ???????-?????????? ?????? https://www.mses-expert.ru/ ???????? ??????????? ???????? ? ?????????? ?????????? ? ?????? ? ?????? ???????? ??????. ???????? ????????? ???????????-???????????, ?????????????, ???????????, ?????????????????? ? ???????????-??????????? ?????????? ?????????? ?????? ?????????. ??????????? ???????? ????????????? ??? ? ??????? ??, ?????? ? ??? ? ?????? ???????? ?????????, ?????????? ????????? ?????????? ??????.
?????????? ?????????? ? ??????? ?????? — ??? ?? ??????
https://tubeqc.com/@leesadenson160?page=about
??????? (???????????) — ???? ?? ???????? ??????????? ?????????? ??? ??????? ????????????-????????????? ???? ?????????????? ??????, ????????????? ???????? ???????????? ???????????? ?????????????? ? ?????????????? ?????????? ????????????. ?? ????? https://indenza.com.ru/ ???????? ??????? ???????? ????????, ?????????, ????????? 40 ? 160 ??, ? ????? ?????????? ?????????? ????? ???????????? ? ???????? ????? ??????. ????????? ? ?????? ???????? ???????????? ?????????, ??? ???????? ????????? ?????????? ??????? ? ??????????? ?????????????? ????????? ???????.
Kraken https://krakencasinotr.com/tr-tr/ Türkiye’nin en iyi online casinosudur. 22 $ yat?r?n ve 77 $ casino bonusu ve 250 bedava dönü? kazan?n! Popüler oyunlara göz at?n veya en sevdi?iniz oyunlar? oynay?n ve büyük ikramiyeyi kazanmaya çal???n! Resmi web sitesinde Kraken Casino’da çevrimiçi oynaman?n tüm avantajlar?n? ö?renin.
?????????? ?????????? ? ??????? ?????? ??????? ?? ?????
https://vincytube.com/@xfuelsie58502?page=about
?????????? ?????????? ??????? ?????? ???????? ?? 2 ???
https://www.invds.uk/jaquelinerimme
??? ???????? ?????????? ????????? 2000 * 30 = 60 000. ?????? ?? ??????????? ????? ?????? ?????? – https://en.gyaanipedia.com/wiki/User:Mckinley03F
??? ???? ???????? ??? ??????????? ? ???? ??????.
??? ???????? ???????? ????, ?? ?? ?????????? ????????, ???????????? ??????????? ??????? ?????????, ????????? ???????? ? ?????????? ??????????????-???????????????.
?????????? ?????????? ? ??????????? ?????? — ????????
https://zhangertong.com/cathleenfreeh
Love the breakdown of slot strategies-super helpful for casual players! It’s always fun to dive into platforms like WinPH99 that mix easy gameplay with great security and a wide game library.
?????????? ?????????? ?????? ????????
https://familyworld.io/@tamiechilds16?page=about
??????? ?????????? ????? ??????????? — ??????? ? 17 ?????? ??????, ???? ??????????? ?????? ??, ???????? ????? ???????????, ????????, ????????, ????????, ??????????? ? ????????? ????, ????????? ????????? ????????? ?????? ? ?????? ??????? ????????. ???? — ??????, ????????? ????????, ?. 30/15, ??. 413, ???????? ????????????? ?????? ? ??????????? ????????????. ?????????? ????? ??????????? ???????, ??????? ?????????????????? ? ?????????? ??????. ???????? ?????????? ?????, ??????? ?????? ? ???????? ????? ? 5–10 ?????: https://advokat-laptinskiy.ru/
?????? ??????????? ??????? ?????? ?? ?????????? ????, ?? ???????????
https://git.emoscape.org/santos93983257
?????????? ?????? ?????? — ??? ?? ?????? ??????
https://git.srv.ink/jeanacovington
????? ??? ??????? ?????????? ?????? ?????? — ??? ??????? ?? ????, ???????
https://gitea.jobiglo.com/gavinmcneal18
Free video chat emerald chat android app and a convenient alternative to Omegle. Instant connections, live communication without registration, usernames, or phone numbers. Just click “Start” and meet new people from all over the world, whenever you like and whatever your mood.
????????? — ??? ????? ??????? ?????? ?????? ?? ??????? ?????? ???? ??????, ? ?? ?? ??????? ??????????. ? ???????? ????????-???????? «???????» ?? ???????? https://www.florion.ru/catalog/mono-bukety ???????????? ?????????? ?????????? ?? ???, ??????? ???????? ? ??? ????????? ? ?????, ? ??? ???????? ???????????. ???????? ????????? ????????? ??????? ? ??????? ??????????? ???????, ???????? ??????????, ??????? ???????? ??????????, ??????? ? ?????? ??????? ? ????????? ?????.
?????? ??????????? ??????? ?????? — ?????????? ???? ????????
https://hellos.link/elip478167
?????????? ????????????? ?????? ?? ??????, ????????? ?? ?????
https://klimaexpress-tube.de/@deannawestgart?page=about
??????????? ???????, ?????????? ??? ??????? ????????? ? ??????, ????? ?? ????? ????????? ????????? ??????? ???????????????? ????????? ?? ??????? ???????? https://booking90.ru/ ???????? ?????????? ?? ??????????? ?????????? ??????????, ???????????, ??????? ? ???-??????? ??? ????? ?????? ? ??????. ??????? ????? ?? ???? ??????????, ??????????? ????????????? ? ??????????? ??????, ????? ?? ???????? ???????? ??????? ??? ??? ?????? ?????? ? ??????????????, ? ????? ??????? ????????? ??? ????????.
?????????? ?????? ?????? — ??? ?? ?????? ??????
https://mirnauk.ru/@maybellecarpen?page=about
Cloud ops optimization: cost savings already kicking in. https://play.pxopro.com/@blondellwekey1?page=about
Incident response drills inspired by your examples. https://quickdate.arenascript.de/@brooke31o4301
??????? ????? ????????? ???? ?????? ???????? — ??? ????? ????? ? ???????????? ??? ???????, ??????? ? ???????? ????????. ????????????? ?????? https://vip-pattaya.ru/ ?????????? ????????? ?????????? ?????????: ?? ???????? ???????? ? ???? ???? ?? ????????? ????? ?? ????????, «???????? ?????????????» ? ????????????? ?????????. ????????? ?????????, ?????????? ?????, ????????????? ????????? ? ??????????? ????????????? ??????? ?????? ??????????? ?????????? ? ??????????, ? ??????????? — ??????????? ? ??-?????????? ?????????????.
Must-Read Collection: https://www.artstation.com/indromogh6/profile
DevOps automation workflows explained perfectly; implementing now. https://reoflix.com/@mollyallison17?page=about
?????????? ??????? ?????? ?????? ?????? ?????
https://onlyaimovies.com/@gpdselina79129?page=about
?????????? ???? ?????? — ?????????? ????
https://qdate.ru/@celesteellswor
????? ???????? ?????????? ?????? ??????, 100%
https://shervas.com/karolynngb6997
???????????? ??????????? ????????, ???????
https://theindietube.com/@bernadine65a8?page=about
?????? ????
kraken ????
?????????? ?????????? ??????? ?????? ???????? ?? 2 ???
https://video.buzzsharer.com/@guadalupewilsm?page=about
?????? ?????????? ????????????? ??????, ???????? ?? ?????????
https://www.camperandgo.it/author/sergioperrier/
????? ? ????? ???????????? ??-??????, ????? ?????? ???????? ?????????? ????? ?? ????????? ?????????????? ???????? ? ???????? ??????. ?? ????? ???????????? ???????? https://ekskursii.open-anapa.ru/ ????? ???????? ???????????? ????????? ?? ????? ? ????? ?????????????? ???? — ?? ?????? ????? ?????-????? ?? «???????? ??????» ?????. ?????????? ??????????, ?????????????? ????????????? ? ??????????? ????????? ?????? ??????? ??????????, ?????????? ? ??-?????????? ?????????????? ??? ???? ?????.
? 2007 ???? ???????? ?????? ??? ??????? SEO ?????????? ????????? ??????? ?? ??????????? ???-???????? ? Google ? Bing. ????? ??????? ??????????? ??????? ?? ????????? private-seo.com/ru/ ??????????? ?????? ?????? ????? ?? ???????????: ??????????? ?????, ?????????? ?????????????? ????????? ???????????, ????????? SEO ? ?????? ? ?????? ???????????? GEO. ?????? ??????? ???????? ??? ???????? ??????????? ?????? ???????????? ? ??????????? ????????? ? ??????????? ???????, ? ??? ??????????????? ?????????? 80% ???????? ?? ?????????? 5-10 ???.
?????????? ????????????? ?????? — ???????? ???????
https://www.smartestwholesale.com/author/ryder72l127378/
??????? ??? ?????? — ??? ?? ?????? ?????? ?????????, ? ?????? ???????, ??????????? ? ????. ????????-??????? http://posteranet.ru/ ???????????????? ?? ????????? ? ???????? ? ?????? ????????, ???????????? ?? ?????? ??? ??????????, ? ??? ??????????? ?????? ? ????????. ???????? ???????? ???????? ?? ???? ??????, ??? ???? ?? ?????? ??? ???????? ??????????, ??? ?????? ??????? ??????? ? ??????????? ???????? ? ????????? ??? ???????? ???????? ???????????? ????, ????? ??? ??????????.
?????????? ????????????? ?????? — ???????? ???????
https://dev.kirill-vorotov.com/donettedouglas/1630744/wiki/tamozhennoe-oformlenie+99W.-
??????????? ?? ????? — ?????????? ?????????? ??????????? ?????? ?????
https://git.avclick.ru/murraywadswort
?????????? ?????????? ?????? ?????? ??????? ?????? ??? ???????
https://git.mkdev.ddns.net/shannonwhitham
?????????? ??????????? ?? ???, ?????? ??? ??????? ? ????? ???????? ????? ? ????????? ??????????? ?????, ??????? ? ??????????????????????? West-atlas.com ?????????? ?????????? ?????? ? ????????? ???????? ?????? ???? ?????? ???????, ????????? ?????? ? ???????? ????????? ??????????? ??????. ??????? ?????????, ???????? ?????????? ????? ????????? ? ?????? ??????? ? ??????? ?????? ???????????? ???????? ??????? ? ??????. ???????? https://west-atlas.com/ ? ???????????? ?????? ????? ????? ????????!
?????????? ?????? — ??? ?????? ? ????????
https://git2.ujin.tech/patrickrenner0
? 2007 ???? ???????? ?????? ??? ??????? SEO ?????????? ????????? ??????? ?? ??????????? ???-???????? ? Google ? Bing. ????? ????? ??? ??????????? ?? ????????? private-seo.com/ru/ ??????????? ?????? ?????? ????? ?? ???????????: ??????????? ?????, ?????????? ?????????????? ????????? ???????????, ????????? SEO ? ?????? ? ?????? ???????????? GEO. ?????????? ????? ????? ?????? ?????? ??? ???????????, ??????????? ?????? ??????? ? ???????? ? ??????? ??????? ?? ????????? ??????-????????????, ??? ???????????? 80% ??????????, ?????????????? ????? 5-10 ???.
?????????? ?????? ?????? — ??? ?? ?????? ??????
https://gitlab.herzog-it.de/horacioknoll21
Just what you need: https://podcasts.apple.com/ky/podcast/puzzlefree/id1697682168?i=1000737822998
?????????? ?????????? ? ?????????? ?????? — ???????? ??????
https://iurl.7s.digital/dongcardenas40
?????????? ??????? ?????? — ?????, ??????, ????????
https://luxurylinkproperties.ae/agents/corrined664077/
The algorithms in an ai rap generator analyze hit songs to understand popular flow patterns.
??????????? ????????? ????????? ?????? ?????? ??? ????????????? ? PGP ???????? ?? darknet ??????? ????? Dread ??? ???????? ??????? ??????????? ?????? ?? ??????????? ??????????????.
???????? ????????? ? ????????????? ????? ??????? ?? ?????? ?????? ??????, ?? ? ?????? ???????? ? ????????? ?????, ? ?????? ???? ????? ???? ???????? ??????? ???????. ?? ????? https://www.nlobova.ru/ ???????????? ?????? ?? ????????, ??????? ?????????, ?????????, ?????????? ? ????????????? ???????? ?????, ? ????? ??????? ?????????? ?????????. ??????? ????? ???? ? ??????, ?????? ???????? ??????????? ?????????????? ? ????????? ????????? ? ????, ????? ???????? ???????? ???????? ? ?????? ?? ?????? ????? ??????? ?????? ??????????? ???????? ? ?????????? ?????????.
?????????? ?????? ?????? ??? ???????? ????
https://namastayrentals.com/author/georginabuck87/
???????????????? ????????? https://stsgeo-spb.ru ??? ????????????? ? ??????????????? ? ?????-?????????? ? ??. ????????-??????? ???????????, ??????????, ???????? ? ???????. ???????? ? ???????? ? ???????? ????????, ?????? ?????????? ?? ???????.
????????-??????? https://stsgeo-krd.ru ???????????????? ?????????? ? ?????????: ???????????, ??????????, ???????????? ??? ?????, ??????????? ? ???????????????. ???????????????? ???????????? ? ??????????? ????????.
????? ?????? ? ??????????? ?????? ?????? ??? ????????? ???????? ? ???? ???????? https://mti5.me/ ? ????????? ??????? ? ????? ???????. ?????? ? ???????????! ????????, ????????? ? ?????? ??????, ?????? ?? ???????? ? ????????? ?? ??????????? ? ?????????? ??????? ? ???? 90 ???? ??? ????????????? ?????????! ??????? ??? ???? ????? ????????????? ?? ?????.
?????????? ?????????? ?????? ?????? — ??? ??? ????, ?????? ?? ?????
https://profmustafa.com/@ilashufelt1925?page=about
?????????? ?????? ?????? — ??? ?? ?????? ??????
https://roadmap.click/kristinwooden2
For hottest news you have to go to see web and on internet I found this web site as a most excellent site for newest updates.
????? ??????
???????????? ???????????? https://stsgeo-ekb.ru ? ????????????? ? ?????????: ???????????, ???????? ??????????, ????????, ???????????. ????????-??????? ??? ????????? ?????????????, ????????? ? ???????. ???????????? ???????????? ? ??????????? ??????.
??????? ?????? ?????? — ??????, ???? ?????????
https://streamz.network/@gingerpigdon9?page=about
????? ??????????? ???????? ??? ?????????? ?????????? ? ??????, ??? ? ???? ?????? https://doskadonbassa.ru/ ?????????? ?????????? ?????????? ? ?????????? ????-????, ????????????, ?????? ? ??????. ??????? ????????? ???????? ?????????? ?????????? ?????????? ? ????????? ? ????????????????? ????????????. ????????? ??????????? ?????? ?????????????? ?????????? ?????? ??? ?????????????? ????????. ??????? ??????????? ? ?????????? ?????????? ???????? ??????? ???????????? ?????????? ?????????!
?????????? ????????? ??????? ?????? — 5 ?????
https://ultimatepropertiesuae.com/author/maplebidmead16/
Uwielbiasz hazard? nv casino: rzetelne oceny kasyn, weryfikacja licencji oraz wybor bonusow i promocji dla nowych i powracajacych graczy. Szczegolowe recenzje, porownanie warunkow i rekomendacje dotyczace odpowiedzialnej gry.
Looking for a specific Raja Luck game? Head over to their download page. They’ve got a bunch of them listed and easy to grab. Here’s the link: rajaluckgamedownload
????? ?????? ? ???? ???? ?????????? ??? ?????????? : ?????? ? ???????? ? ???????, ?????????? ?? ??????????, ????-?????????? ? ??????. ???????? ???????? ? ???, ??? ????? ????? ?? ????? ????? ??? ? ???????????? ? ????????.
???????????? ?????? ??? ???????, ??????? ?? ?????????? ?????????? ???????????? ??????
https://wedioz.com/@pedroguess472?page=about
?????????? ?????????? ??????????? ?????? — ??? ?????
https://www.ngiafon.com/video//@grettajyp81499?page=about
????? ???????? ???????? ? ????? ???????????? ????????, ? ??????? ????? ?? ?????? ????????, ?? ? ??????????? ?????????? ??????? ??????. ????????? https://store-dubai-drinks.com/ ?????????? ??????????? ?????? alcohol delivery: ??????????????? ??????, ??????????? ????????? ?? ????? ?????? ? ???????????? ????? ?? ????? ? ??????? ?? ??????????? ? ????. ?????? ???????, ???????? ??????? ? ?????? ?? ??????????????? ?????? ?????? ??????? ??? ??? ??????????, ??? ? ??? ?????? ???????, ??????? ???????, ??????????? ? ??????? ??????? ???????.
????????????? ?????? ??? ????? ? ???????? ??????????? ??????????? ???? ? ????????. ?????? ??????, ??? ????????, ?????? ??????? ?????. ???????? ??????? ????? ?????? ?????????? ?????. ???????? ???? ??????? ? ???????. ???????? ?????? ???????????? – ?????? ????????? ?? ?????
????? ?????? ? ???? ????? ???? ?????????? ? ??? ?????? ? ????????? : ?????? ? ???????? ? ???????, ?????????? ?? ??????????, ????-?????????? ? ??????. ???????? ???????? ? ???, ??? ????? ????? ?? ????? ????? ??? ? ???????????? ? ????????.
?????????? ?????? — ??? ?????? ? ????????
https://compass-estate.com/uk/estate_agent/kishalowes877/
?????????? ??????? ?????? ?????? ?? ??????
https://fs-biolink.com/nicolasclutter
????? ? ????? ???????????? ??-??????, ????? ?????? ???????? ?????????? ????? ?? ????????? ?????????????? ???????? ? ???????? ??????. ?? ????? ???????????? ???????? https://ekskursii.open-anapa.ru/ ????? ???????? ???????????? ????????? ?? ????? ? ????? ?????????????? ???? — ?? ?????? ????? ?????-????? ?? «???????? ??????» ?????. ?????????? ??????????, ?????????????? ????????????? ? ??????????? ????????? ?????? ??????? ??????????, ?????????? ? ??-?????????? ?????????????? ??? ???? ?????.
?????????? ?????????????? ?????? ??? ??????, ?????? ??? ??? ??????
https://git.infortek.tech/zzqdonald30016/donald2011/wiki/tamozhennoe-oformlenie+68G.-
???????? ?? ???????? ????? https://www.chitai-gorod.ru/catalog/toys/lego-115391 ? ?? ??????? ?????? ???????????? LEGO ? ??????? ????????????, ? ????? ?????? ??? ??????? ??????????? LEGO ??? ???????. ?????????? ?????????? ????? ????????????? LEGO ? ?? ??????????? ??????? ?? ??? ??? ??????????!
?????????? ?????????? ?????? ????????
https://git.thunder-data.cn/michelavery918/michel1998/wiki/tamozhennoe-oformlenie+82n.-
???????? Waltzprof ??????????? ???? ????????? ?? ???????????? ????????? ??????? ? ?????? ????????? ???????? ???????? ??? ???????, ??????????? ? ?????. ?? ????? https://waltzprof.com/ ???????????? ?????????? ??????? ?? ???????????? ? ??????????? ?????, ?????????????? ??????, ??????? ????? ? ????????????? ??????????? ?????? ????????????. ??????????? ???????? ?????????? ?????????? ? ??????? ????????? ????????, ??????? ??????????????? ? ?????????? ???????? ???????? ??????? ??? ??????? ???????? — ?? ??????? ??????? ?? ??????? ?????, ??? ????? ?????????????, ???????? ? ?????? ???????? ?????????.
????? ?????????? ???????????? ? ????????? ? ???? ?????? ? ?????? ? ???????? ???????? ???? https://krab1.ru/ – ????????? ?????????? ??? ???? – ????, ????????, ????, ??????, ??????? ????????, ? ?? ???????? ??? ??????? ? ??????????? ?????????? ? ????????????? ? ???????? ??? ???! ? ??? ?????????? ??????????? ??????? ????? ? ????? ??????? ? ????????????. ????????? ?? ?????.
What’s up to all, how is the whole thing, I think every one is getting more from this web site, and your views are good for new people.
escorts Rio
?????? ?? ?????? — ?????????? ?????????? ?????? ?????? ?????? ??????
https://gitea.offends.cn/caitlyncastano
?????????? ?????? ??? ??????? ????????
https://hostseeker.store/@garfieldlawson?page=about
????? ????????? ???? ? ????????? ?? ?????? ? ?? ?? ???????? ????? ???????? https://xn—-8sbwhzjq7b3a.xn--p1ai/ ? ?? ??????? ??????? ??????????? ?????, ??? ?????? ????????? ??? ??????? ? ?????????????? ?????????. ??????? ?????, ?????????????? ?????? – ???????? ???? ? ??? ? ????????? ?????? ? ??????!
??????? ????? ????????? https://vash-elektrik24.ru ?? ??? ? ??????. ??????? ? ??????? ????, ?????? ?????? ? ???????? ?????????????, ??????? ???????, ????????, ?????. ?????????????? ?????, ???????? ?? ??????, ?????????? ???? ??? ??????? ??????.
???????? ????????, ?????? ???????? ?????????? ?????????? ??????, ??????????
https://learninghub.fulljam.com/@karachipman47?page=about
?????????? ?????????? ? ??????? ?????? — ??? ?????
https://mozatoday.com/@kandice869733?page=about
Hot Topics: https://addthismark.xyz/story.php?title=from-search-to-success-my-journey-to-buy-facebook-ad-accounts-that-deliver
??? ??? ???? ? ????????????? ???????. ???? ?????? ???????: ???????? ???????, ???????????? ???????? ? ????? ??????????. ??????????? ???????? ? ???????????????? ??????. ??????????? ??? ??????????? ? ????? ?????! https://tattooator.ru/
?????????? ?????????? ??????????? ?????? ?????? ? ??? ????????
https://pl-property.com/author/lucas76m367708/
?????? ??????????? ??????? ?????? ???? ?????? ??????
https://rc.intaps.com/thaliafarthing
?????????? ??????? ?????? — ????? ? ?? ??????
https://sm99.co/@zaracousins000?page=about
?????????? ?????????? ?????? ?????? — ??????? ??????, ??? ??
https://topnova.properties/author/rickiecaban859/
?????????? ????????????? ?????? ?? ??????, ????????? ?? ?????
https://vidmero.com/@sanfordstukes?page=about
??????? ?????? ?????? — ?????? ???? ? ?????
https://www.grupposolutio.it/agents/maryannelovele/
Engagement metrics matter significantly when you buy tiktok likes for marketing campaigns. Authentic interaction signals improve For You Page placement helping content reach broader audiences organically beyond initial purchased engagement.
?????????? ?????? ?????? ??????? ?????????? ?????? ????????? ? ??????? ?????????, ??????????? ?????????? ? ?????????????? ?????????? ?????? ???????????.
????? ?????????? ?????? ? ??????? ?????????? ????? ?? ????????????, ??? ???????? ???????????, ????????? ?????????? 1Win ???????????? ? ??????????? ?????????? ??? ???????? ?????????????. ?? ?????? https://t.me/s/win1win_skachat_na_android ????? ??????? ??????????? ?????? 1win ??? Android ? ???????? ? ??????? ?????? ?????????? ???????????? ?????????: ?? ????? ? ????-?????? ?? ??????? ???????? ? ??????? ????????. ??????? ?????????, ?????????????? ??? ?????????, ??????? ?????? ? ??????????? ??????? ?? ????????? ? ????? ????? ?????? ?????????? ???????? ??????? ??? ???, ??? ????? ????????, ???????? ? ??????? ? ???? ??????-??????.
??????????? Tor ??????? ???????????? ?????? tor ?????? ????? ????????????????? ????????? ???????????? ? ??????????? JavaScript ? ??????? ????????? ?????? ??????? ?? ?????? ?????????.
???????? ?????? ???????? https://88000.com.ua ??????? ????? ?????, ????????, ?????????, ????????, ????? ?? ????? ???????. ?????????? ??????, ?????????, ??????’? ?? ?????????. ??? ??????? ??? ??????? ? ?????? ?????, ?????? ? ???????? ?? ????’?????.
?????????? ?????????? ??????????? ?????? ??? ?????????
https://www.zambianhome.com/author/lancaperton079/
A cozy hotel Bianca Kolasin for mountain lovers. Ski slopes, trekking trails, and local cuisine are nearby. Rooms are equipped with amenities, Wi-Fi, parking, and friendly staff are available to help you plan your vacation.
?????????? ?????????? ?????? ?????? — ??? ????????? ? ??????
https://estatesbazaar.com/author/niiwolfgang526/
???????? ??????????? — ?????????? ?????????? ? ??????????? ?????? ??? ????????
https://git.comzg.com/theodore495804
?????? ????
kraken darknet
?????????? ?????????? ? ?????????? ?????? — ?????????? ? ????????
https://git.repo.in.net/terrellumbagai
?????????????? ?????? «??????????????? ?????????» ???????? ?? ????? ???????? ???????? ?? ???? ?????? ? ?????????? ????? ????????? ?? ?/?-?????????? ? ???????? ? ????????????????? ???????. ?? ??????? https://gdlog.ru/ ???????????? ?????? ???? ?? ????? ??????????? ? ????? ?????? ?????????? ??????????, ??????????????? ?? ???????? ? ??????? — ?? ?????? ? ?????-?????????? ?? ??????????????? ? ????????? ???????. ??????? ?????????, ???????? ????? ??? ???????? ? ??????????? ???????? ???? ??????? ?????? ?????? ??????? ???????????? ??? ???????, ??????? ????????? ????????? ??????????? ??????? ???????? ?? ???????? ??????.
?????????? ?????? ?????????? ???????, ??? ???????
https://gitea.ddegame.cn/brunocordova68
?????? ?? ????? ?????? — ??? ???????????? ???????, ??????? ?????????? ????? ? ????????? ???-??????. ? ????????-???????? «???????» ?? ???????? https://www.florion.ru/catalog/loshadi-iz-cvetov ?? ??????? ?????????????? ??????????, ????????? ??????? ?? ?????? ??????? ? ??????. ????? ?????????? ???????? ????? ?? ??????? ??????????, ??????? ? ???????????? ????????????: ??? ?????????? «???-??????», ??????? ????????? ? ????????? ? ????? ????????? ?????????? ??????? ???, ??????????? ?????? ? ???? ????????.
??????????? ????????? ??????? ??????? ????????? ?????????? ? ?????????????? ??????? ? ???????????? ??????????. ???????????? ???????? «????? ?????????» ?????????? ?????? ????????? ? ?????????????? ? ????????????????? ?????????? ??? ????? ?????: ????????????? ???????????, ??????, ???????? ????????? ??? ???????? ?????????. ?????????????? ????????????? ?????? ???????????? ????????????? ?????? ??????? ?????????? ?????????? ?? ??????? ????. ?? ????? https://anapa-transport.ru/ ????? ???????????? ? ???????? ? ???????? ???????? ??? ????????????? ???????, ??????? ??????????? ??????????????? ??????????? ? ???????? ???????? ?????.
kraken ???????
kraken8
???????? ?????????? ?????? ??????, ???????? ?? ?????? ???
https://gt.clarifylife.net/manualpelensky
Premium alcohol delivery ? ????? ????? ???????? ???? ???????? — ??? ???????? ???????? ??? ???, ??? ?? ????? ??????? ????? ?? ?????? ?????? ????????. ?????? https://drinks-delivery.com/ ????????????? ???? ??? ???? ?? ????? ???????? ??????????????? ???????? ??????, ??????? ??????? ??????????? ????, ???? ? ???????? ???????? ? ?????? ????????? ?? ?????. ?????? ???????? ????????? ?????????? ???????? ???????????????? ? ???????????? ????????, ? ??????? ??????-??????? ???????? ???????? ????? ?? ???? ?????, ?? ??????? ????????? ??????.
?????????? ?????????? ? ??????? ?????? — ?????? ? ?????
https://kenyahomeshub.com/author/heatherrodarte/
kraken ???
kraken ??????
Casino utan registrering https://casino-utan-registrering.se bygger pa en snabbare ide: du hoppar over kontoskapandet och gar direkt in via din bank-ID-verifiering. Systemet ordnar uppgifter och transaktioner i bakgrunden, sa anvandaren mots av en mer stromlinjeformad start. Det gor att hela upplevelsen far ett mer direkt, tekniskt och friktionsfritt upplagg utan extra formular.
Free Online Jigsaw Puzzle https://yandex.com.tr/search?text=puzzlefree.game play anytime, anywhere. Huge gallery of scenic photos, art and animals, customizable number of pieces, autosave and full-screen mode. No registration required – just open the site and start solving.
?????? ??????????? ??????? ?????? — 10 ?? 10
https://meeting2up.it/@eldonkirby115
Casino utan svensk licens https://casinos-utan-licens.se ar onlineplattformar som drivs av operatorer med licens fran andra europeiska jurisdiktioner. De erbjuder ofta ett bredare utbud av tjanster och anvander egna regler for registrering och betalningar. For spelare innebar detta andra rutiner for sakerhet, verifiering och ansvarsfullt spelande.
I casino crypto https://crypto-casino-it.com sono piattaforme online che utilizzano valute digitali per transazioni rapide e sicure. Permettono di vedere in pratica i vantaggi della blockchain: trasparenza dei processi, assenza di intermediari, trasferimenti internazionali agevoli e un’interfaccia moderna, pensata per un’esperienza tecnologica degli utenti.
???? ??????????? ???????, ??? ? ??????, ?????????? ???? ??????
https://offplanluxury.com/author/moseabrams875/
?????????? ?????????? ? ??????? ?????? ??????? ?? ?????
https://propertymanagementhuahin.com/author/lizetteufx9625/
?????? ??????
kraken ??????
??? «??????» ??????????? ??????????? ???????????? ???????? ? ??????? ???, ????? ???????? ????? ??? ??????? ??? ??????, ???????? ????????. ?? ????? https://denors.ru/ ???????????? ??????? ??? ???????????????, ???????-???????? ???????????, ????, ????????? ? ???????????? ????????? — ?? ???????????? ? ??????? ?????????? ?? ?????? ? ???????. ???????? ?????????? ???????, ?????? ? ??????, ? ????? ? ?????? ?????? ???????????? ???????????? ?????????, ???????? ??????? ? ??????????? ???????? ???????????????? ??????? ?????? ??? ?????? ??????.
?????? ??????????? ??????? ?????? ?? ?????????? ????, ?? ???????????
https://senexhomes.com/agent/nellcolley3185/
kraken market
kraken ????
Explore hyperliquid aggregator and gain unlimited access to a modern, decentralized market. Trade derivatives, manage your portfolio, utilize analytics, and initiate trades in a next-generation ecosystem.
Use hyper trading for stable and efficient trading. The platform combines security, high liquidity, advanced solutions, and user-friendly functionality suitable for both beginners and professional traders.
Discover hyperliquid dex a platform for fast and secure trading without intermediaries. Gain access to innovative tools, low fees, deep liquidity, and a transparent ecosystem for working with digital assets.
Choose hyperliquid arbitrage finder as a convenient tool for trading and investing. The platform offers speed, reliability, advanced features, and fair pricing for cryptocurrency trading.
A cozy swissotel Kolasin for mountain lovers. Ski slopes, trekking trails, and local cuisine are nearby. Rooms are equipped with amenities, Wi-Fi, parking, and friendly staff are available to help you plan your vacation.
Choose hypertrade — a platform for traders who demand speed and control: over 100 pairs per transaction, flexible orders, HL token staking, and risk management tools. Support for algorithmic strategies and advanced analytics.
Check out multi hop routing hyperliquid, a modern DEX with its own L1: minimal fees, instant order execution, and on-chain transparency. Ideal for those who want the speed of a CEX and the benefits of decentralization.
?????????? ?????? ?????? ??? ???????? ????
https://tapm.ee/nevareibey3135
?????????? ??????? ???????? ??????? ? ??? ?????? ????? ?????: ???????????? ?? ?????????, ?????????? ? ?????? ??????????, ????????? ???????????? ????????, ?????????? ??????? ???, ?????? ? ???????? ?????????????? ?????, ????????? ???????????? ? ??????????????????? ?????????. ???????? ??????????????????.
?????? ??????? ???????? ???? ??????????? ?????? ???????? ?????: ????? free zone, ??????????? ????????, ??????????????, ??????? ?????????, ?????????? ???? ? ???????????. ?????????? ???????, ??????? ????? ? ????????????? ?? ??????? ??????? ???????.
?????? ??????
kraken darknet
??????? ?????? ?????? — ?????? ? ???????
https://vainend.com/virgilzinn8092
kraken ???????
kraken ???????????
?????????? ???????? ????????? ??? ??? ?????????????? ???????: ?????? free zone ??? mainland, ?????????? ????????? ????????, ?????????? ????????????? ??????????, ??????????????, ?????????? ????????????? ? ????????? ?? ???????. ?????????????????? ? ?????????? ??????? ??????.
?????? ????? ?????? ????? ??? — ?????????? ?????????? ??? ?????? ??????? ? ??????????????? ????????????. ???????? ??????? ?????????, ??????????? ?????????, ???????????????? ????, ?????????? ??????????????????, ?????????? ? ???????????? ????????????? ???????????.
???????????????? ?????????? ???????? ?????? ???: ?? ?????????? ????????? ?????????? ???????? ????????? ? ?????? ?????????? ?? ???????????, ??????????, ????????? ?????????? ????????? ? ????????????? ?????????????? ????????. ?????? ?????????????????? ? ?????? ????????? ?????.
?????? ??????? ????? ???????? ??????????? ????? ? ??? ????????? ??????????? ????, ???????? ?????????, ??????? ? ??????????, ???????????? ???? ??????? ?? ????????? ????????. ???????????? ????????????????, ?????????? ? ?????????? ? ?????? ???? ??????????.
?????????? ?????????? ??????????? ?????? — ??? ????????
https://www.aytacproperties.com/agents/wilfredohutchi/
????? ???????? ????? ???? ?? ?????
https://bravomos.ru/ bravomos
????? ?????? ??????? ????????? ? ???????? ???? xn—-itbqgfcdcbm0a.xn--90ais – ??? ?? ??????? ???????????????? ?????? ? ???? ?????????. ??????? ???? ??????, ????????? ? ??????? ?? ???????? ? ???????? ?? ??????. ???? ?????? ?????????? ????????? ? ???????????? ?????????, ? ???? ????? ???????? ????????? ???????????? ?????? ????? ?????????. ???????????, ??????????????? ??? ?????? ????????? ??? ?????????????. ?????? ? ??????? ?????? ??? ???? ??????????.
?????????? ??????? ?????? — ??????, ?????, ????????
https://www.qbrpropertylimited.com/agent/wandabrunson33/
«??????????» ????????? ???????? ???????????? ?????? ?? ???????? ? ?????????? ???????, ??? ????? ? ????????, ? ?????????. ?? ????? https://belblokopt.ru/ ??????????? ???????? ??????? ?????????? ? ?????????????? ?????? ??? ????, ?????? ? ???????????, ??????? ????????? ??????? ??? ? ?????????? ??? ? ??????? ??????? ?????????. ???????? ?????????? ???????? ? ?????????, ????????????? ?? ?????? ????????? ? ???????????? ????????? ?? ???????? ? ????????????, ???????? ??????? ???????????? ? ??????????? ???????? ??????????? ??????????? ???????? ???????? ?? ?????????????, ??? ?????? ???????? ? ??????.
?????? ??????????? ???? ???? ??? ????????? ?????? ????? ????????????? ? ??????????? ?? ??????, ????????? ???????? ? ?????? ????????????. ????? ???????? ??????????? ???????? ? ???? ?????????? ????, ????? ??? ??????? ???????? ??? ?????? ?? ???????? ???????. ????? ???????? ????????? ?????? ?????? ? ????, ??? ????? ??????????? ????????, ?????? ???????? ? ?????????? ???????????. ????? ???????? ????????? ?????? ????? ???????? ?????? ??? ??????????, ? ????? ???????????? ??????? ?? ??????? ?? ????????? ????????. ????? ????????? ????? ???????, ??????? ????? ?? ?????? ???????????, ?? ? ???????????, ????? ?????? ???????? ?????????? ???? ????????? ? ??????????? ?????????.
?????????? ?????????? ??????????? ?????? — ??? ???????? ?? ???????
https://dating.hyesearch.com/@jasongatty045
????? ????? ??????? ???? ? ??? ??? ????: ???????? ??????????, ???????? ? ?????????????, ????????? ?????????? ?? ??????, ???????????, ?????? ?????? ? ?????? ???????????? ????. ???????????? ???? ??????? ? ???????? ?????? ???????? Emirates ID.
??????????? ???????? ?????????? ???: ??????????? ????? ??????? ??????????, ?????????? ????? ??????????, ????????? ??? ??????? ? ?????????? ????????, ?????? ???? ?????????? ? ?????????????. ??????????? ???????????? ? ?????????? ???? ????.
????????????? ????????? ????? ? ??? ??? ????: ?????? ????????????? ?????????, ????? ?????? vesting, ?????????? ????????? ??????????, ????????? ???????? ?????? ? ?????? ?????. ???????? ????????? ?????????? ? ???????? ??????? ???????????? ????????? ???????.
Corporate corporate bank account opening in dubai made simple: we help choose the right bank, prepare documents, meet compliance requirements, arrange interviews and support the entire onboarding process. Reliable assistance for startups, SMEs, holding companies and international businesses.
Get your uae golden visa with full support: we analyse your profile, select the right category (investor, business owner, specialist), prepare a compliant file, submit the application and follow up with authorities. Transparent process, clear requirements and reliable guidance.
??????
?????? ???????
??????? ?? ???????????????? ?????????? ????????????? ??????
https://git.7milch.com/janelleloveles
Professional set up company in uae: advisory on jurisdiction and licence type, company registration, visa processing, corporate bank account opening and ongoing compliance. Transparent costs, clear timelines and tailored solutions for your project.
Comprehensive tax consultant uae: advisory on corporate tax, VAT, group restructuring, profit allocation, substance and reporting obligations. We provide practical strategies to optimise taxation and ensure accurate, compliant financial management.
Comprehensive consular support uae: embassy and consulate liaison, legalisation and attestation of documents, visa assistance, translations and filings with local authorities. Reliable, confidential service for expatriates, investors and corporate clients.
Trusted accounting services in uae providing bookkeeping, financial reporting, VAT filing, corporate tax compliance, audits and payroll services. We support free zone and mainland companies with accurate records, transparent processes and full regulatory compliance.
Want to obtain an investor visa uae? We guide you through business setup or property investment requirements, prepare documentation, submit your application and ensure smooth processing. Transparent, efficient and tailored to your goals.
????? ????????????? ????? ? ????????????? ??? ???? ??? ?????? ???????? ???????? https://premium-sk.ru/ – ??? ?? ??????? ??????? ???????? ????? ?? ??????????????. ???????????? ? ????? ???????????? ????????? ??? ??????????? ?????????, ? ?????? ????? ????? ???????????. ???????????? ???????? ?? ??????. ? ??????? ????????? ? ?????? ????????? ?? ????? ?????? ???????????? ????? ? ???????. ????????? ?? ?????.
?????? ???????
kraken8
End-to-end corporate setup uae: company formation, trade licence, corporate documentation, visa processing, bank account assistance and compliance checks. We streamline incorporation and help establish a strong operational foundation in the UAE.
Launch your fund setup uae with end-to-end support: structuring, legal documentation, licensing, AML/KYC compliance, corporate setup and administration. We help create flexible investment vehicles for global investors and family wealth platforms.
Set up a holding company in uae with full legal and corporate support. We help select the right jurisdiction, prepare documents, register the entity, coordinate banking and ensure compliance with substance, tax and reporting rules for international groups.
Comprehensive family office setup uae: from choosing the right jurisdiction and legal structure to incorporation, banking, policies, reporting and ongoing administration. Tailored solutions for families consolidating wealth, protecting assets and planning succession.
Need legalization of documents for uae? We manage the entire process — review, notarisation, ministry approvals, embassy attestation and translation. Suitable for business setup, visas, employment, education and property transactions. Efficient and hassle-free.
???????????? ?????? ??? ???????, ??????? ?? ?????????? ?????????? ???????????? ??????
https://git.lmbrs.org/valoriemonroy4
Need a poa dubai? We draft POA documents, organise notary appointments, handle MOFA attestation, embassy legalisation and certified translations. Ideal for delegating authority for banking, business, real estate and legal procedures.
Need a will uae? We help structure inheritances, appoint executors and guardians, cover local and foreign assets and prepare documents in line with UAE requirements. Step-by-step guidance from first consultation to registration and safe storage of your will.
Open a brokerage account uae with full support. We review your goals, recommend regulated platforms, guide you through compliance, handle documentation and assist with activation. Ideal for stock, ETF, bond and multi-asset trading from a trusted jurisdiction.
Complete uae work visa support: from eligibility check and document preparation to work permit approval, medical tests and residence visa issuance. Ideal for professionals moving to Dubai, Abu Dhabi and other emirates for long-term employment.
?????????? ? ????? https://chinaavia.com ?? ???????? ?????: ??????? ????? ??????, ????????? ???????, ?????? ? ??????????? ????????, ?????????? ??????????. ?????????? ?????? ? ?????, ??????, ???????? ? ?????? ?????? ??????. ???????? ?????? ? ?????????? ?????? ???????????? ??????.
?????????? ?????????? ? ??????????? ?????? — ??? ????????
https://git.xemo-net.de/danniellekaest
Verified service site shop is proud to present direct access to buy top-tier accounts suitable for business. The pride of our service is our exclusive educational hub, featuring secret guides on SMM. Inside the guides, experts share tips on using trackers to increase profits in your daily work. Ordering from us, you get not only working goods, but also helpful tech assistance, replacement warranties and the lowest prices in the industry.
????? ????? ???????? ?? ????????????? ???????? ???? https://www.mezhgorod-taxi-novosibirsk.ru/ ? ?? ??????? ???????? ??????? ?? ???????????? ? ????????? ????????? ?? ????? ? ?????? ?????? ??????. ?? ????? ???????? ??????? ??????????? ? ????????? ??????? ?? ?????????? ????????. ?????????? ??????? ?????? ? ????????? ?? ??????????. ????????? ?? ?????.
?????? ?? ????? — ?????????? ?????????? ?????? ?????? ??? ????????
https://gitea.ultrasoft.cm/scottgok006598
? ???? ??????? ???????? ??????? ?? ?????? ?????????? ????, ?? ? ???????? ?????????, ? ????? ??????? ???????? ????????????? ?????. https://fortuna-distillery.com/ ????????? ??????? ?????????? ??????? ??????? ? ??????????? ?????????? ??? ???????? ?????????? ??????. ?? ????? ??????????? ??????? ?? ??????? ??????? ??????????? ??????????? ????????.
???????? ????????? ? ????????????? ????? ??????? ?? ?????? ?????? ??????, ?? ? ?????? ???????? ? ????????? ?????, ? ?????? ???? ????? ???? ???????? ??????? ???????. ?? ????? https://www.nlobova.ru/ ???????????? ?????? ?? ????????, ??????? ?????????, ?????????, ?????????? ? ????????????? ???????? ?????, ? ????? ??????? ?????????? ?????????. ??????? ????? ???? ? ??????, ?????? ???????? ??????????? ?????????????? ? ????????? ????????? ? ????, ????? ???????? ???????? ???????? ? ?????? ?? ?????? ????? ??????? ?????? ??????????? ???????? ? ?????????? ?????????.
?????????? ????????????? ?????? — ???????? ???????
https://inmessage.site/@george75247359
???????? ????????, ?????? ???????? ?????????? ?????????? ??????, ??????????
https://listflips.com/author/grettaharness7/
?????????? ?????????? ??????????? ?????? ?????? ? ??? ????????
https://mycrewdate.com/@darwinrosman7
?????????? ?????????? ??????? ?????? ?????? ? ??? ??????
https://playtube.theapp4u.com/@educurtis64137?page=about
?????????? ????????? ??????? ?????? — ?????
https://repo.apps.odatahub.net/hassieligertwo
??????? ? ????? ????? ????????? https://rutiti.ru/a-ljpost/login-okolyako/frl-5 ??????? ???????? ? ?????, ????? ?????????? ??? ????? ? ????, ? ?? ??? ????????? ??? ??? ???????, ??????.
Platforma internetowa mostbet: zaklady przedmeczowe i na zywo, wysokie kursy, akumulatory, zaklady na sumy i handicapy, a takze popularne sloty i kasyno na zywo. Bonus powitalny, regularne promocje, szybkie wyplaty na karty i portfele.
Descubre cocoa casino online: tragamonedas clasicas y de video, juegos de mesa, video poker y jackpots en una interfaz intuitiva. Bonos de bienvenida, ofertas de recarga y recompensas de fidelidad, ademas de depositos y retiros rapidos y un atento servicio de atencion al cliente. Solo para adultos. Mayores de 18 anos.
?????????? ?????????? ?????? ?????? — ??? ????????
https://spinvai.com/markhargraves
???????? «????? ?????» — ??? ?? ?????? ?????????? ?????, ? ????????? ??????????? ????? ???? ?? ??????? ????? ? ?????, ????? ???????, ??????-???? ? ???????????. ?? ????? https://volgaglamp.ru/ ????? ??????? ???????? A-frame ???? ??? ?????????? ??????? ? ?????????, ?????? ? ??????? ?????, ????????????? ????? ? ????????????? ? ???????? ? ?????????????. ????? ???? ?????????? ? ????? ???? ? ???? ?? ????, ???? — ???????? ? ???????? ????? ????, ??????? — ?????, ?????? ? ?????? ?????????? ?? ?????????? ????. ?????? ????????? ????????? ?????????? ????? ??????? ? ??????? ???????? ??????? ?????.
?????????? ?????? ?????? ?????? ?????? ? ???, ?????????
https://tubisocial.com/@mindyhewlett8?page=about
Prodej reziva https://www.kup-drevo.cz v Ceske republice: siroky vyber reziva, stavebniho a dokoncovaciho reziva, tramu, prken a stepky. Dodavame soukromym klientum i firmam stalou kvalitu, konkurenceschopne ceny a dodavky po cele Ceske republice.
Professional data backup europe secure, efficient, fast and privacy-focused reliable FTP Backup storage in Europe. 100% Dropbox European alternative. Protection on storage account. Choose European Backup Storage for peace of mind, security, and reliable 24x7x365 data management service.
????????? ?????? ??? ??? ? ??????? ??????? ?? ??????? – ??? ?????????? ?????????????? ? ?????. ?? ???????????? ????????, ?????????????? ??????? ??????, ?? ??????? ?????????? ?????? ??? ????????? ??????, ?? ???????? ??????????? ?? ???????? ???????? – ????? ?????? ??????? ?????? ????? ??? ??????????? ??? ???????? ?????????? ? ???????????????? ??????. ?????? ???????? ????? ??????? ???????? ?? ??? ??????, ?????????? ??????????? ?????????? ??????.
???????? ????????? ????????? ????? ??????????? ??? ??????? ??????-??????? ???????????? ??????????? ? ???????? ????????. ??????????? Platl.ru ???????????????? ?? ??????? ???????????? ?????? ?????????, ?????????? ???????????? ? ???????? ??????? ??? ????????? ????????. ? ???????? ???????????? ????? ??? Steam, App Store, Xbox, ?????????? ??????? ?????????, ? ????? ???????? ??????????? ??????????? ??? ??????? ? ??????????. ????????? ?? https://platl.ru/, ????? ????? ?????? ??????? ?? ???????? ???? — ?? ??????????? ?? ???????-???????? ?? ?????????? ???????. ??? ?????? ???????????? ????????? ????? ?????? ? ??????????? ????.
????? 777 ??????????? ???? ????????? ????? 777 – ??? ?????????? ??????-?????????, ???????????? ??????? ????? ???????? ???, ??????? ??????? ????????, ????????? ???? ? ???????. ????????????? ???????? ??? ?????????? ????-??????, ??? ? ???? ?? ???????? ??????.
?????????? ???? ?????? — ?????????? ????
https://vw-git.senecasense.com/carolerwin7094/carol2023/wiki/tamozhennoe-oformlenie+51M.-
??? ???, ??? ????? ????? ? ??????? ? ??????, ?????? «????? ? ???????? ? ?????» ?????????? ??????????? ?? ??????? ???????????? ?????? ?? ????????? ? ?? ??? ?????????. ?? ????? https://anapa-taxi-transfer.ru/ ????? ??????? ?????????? ????????? ???????, ??????? ??????? ?? ?????????, ?/? ???????, ???????? ?????????????? ???? ? ?????, ? ????? ???????? ???? ??????????? ??????. ?????????????? ??????, ????????????? ?????? ? ??????? ???????? ?????????? ?????? ? ????????? ??????????? ???????, ? ?? ? ?????????? ???????????.
?????????? ?????? ?????? — ??? ?? ?????? ??????
https://www.masercondosales.com/agents/lupebeard0580/
????? ????????? https://vash-elektrik24.ru ?? ??? ? ??????: ??????????? ?????, ????? ? ?????????? ??????????????, ????????? ??????? ? ????????????, ??????????? ???????, ?????? ????????. ????????????????? ???????, ?????? ????, ???????? ?? ?????? ? ??????? ????? ???????.
?????? ????? ????? vykup-auto78 ?????? ? ?????????: ???????????? ??????, ????? ???????????, ?????????? ?????? ? ?????????? ??????? ????????? ??? ?? ?????. ???????? ?????????? ???? ????? ? ?????, ??????? ????? ? ????? ???. ???????? ??? ??????? ????????.
University https://vsu.by offers modern educational programs, a strong faculty, and an active student life. Practice-oriented training, research projects, and international collaborations help students build successful careers.
?????????? ?????????? ??????????? ?????? ??? ?????? ??????????
https://zurimeet.com/@jurgenfritz095
??? ???, ??? ??????? ?????? ?? ???????? Kraken.
?????? ??????? ??? ??????, ??????????? ???.
???????? ? ????????.
Keywords: kraken ??????? ?????? onion, ???? kraken darknet, ?????? ????? ???, ?????? darknet, kraken ???????, ?????? ??????.
kraken ?????? ???????
??? ???, ??? ??????? ?????? ?? ???????????? Kraken.
??????????? ?????? ??????????.
??????????? ???? ????????.
?????? ???: kraken darknet, kraken ?????????? ??????, kraken ????? ???, ?????? ??????? ??????, kraken ?????? ???????, ?????? ??????.
???? kraken darknet
???????? Waltzprof ??????????? ???? ????????? ?? ???????????? ????????? ??????? ? ?????? ????????? ???????? ???????? ??? ???????, ??????????? ? ?????. ?? ????? https://waltzprof.com/ ???????????? ?????????? ??????? ?? ???????????? ? ??????????? ?????, ?????????????? ??????, ??????? ????? ? ????????????? ??????????? ?????? ????????????. ??????????? ???????? ?????????? ?????????? ? ??????? ????????? ????????, ??????? ??????????????? ? ?????????? ???????? ???????? ??????? ??? ??????? ???????? — ?? ??????? ??????? ?? ??????? ?????, ??? ????? ?????????????, ???????? ? ?????? ???????? ?????????.
??????? ???????? ??????? ?? ???? ?????????? ?????? ???????? ???????? ?????? ??? ???????. ??????? ????? ?????? ??????? — ??? ??????? ?????????? ??????????, ??? ???????? ??????? ?????????? ?? ?????????. ?? ???????, ????? ??????? ????????? ??????? ????????, ??? ???????? ??? ? ????? ??????????? ??????. ??????? ?????, ?? ????????? ?? ?????? ????, ? ????? ?????? ????????????, ????????? ?? ???? ? ??????????? ??????? ???? ?? ?????.
?????????? ?????????? ??????? ?????? ???????? ?? 2 ???
https://flowndeveloper.site/@jerricolmenero
??????? Apple ? ?????? https://app-house.by/ – ??? ???????????? ??????? Apple, ? ??? ????? iPhone, iPad, MacBook, Watch, ?? ???????? ????. ???????? ?? ???? ? ?? ??????? ?????? ?????, ?????? ?? ????????? ????????????. ? ??? ?? ??????? ??? ????? ?????????? ????????. ????????? ?? ?????.
?????????? ?????????? ? ??????????? ?????? — ????????
https://git.gezhishirt.club/heathukv995607
?????? ????????? ??????? ????? ??? ?????? – ??? ???????? ?????????? ????? ????????? ??????, ??? ???????, ????????, ?? ???? ???????? ???????? ???????? ? ????????, ?? ??? ????? ? ???????? ????????? ? ?????????? ????? ????????. ?????????? ????, ?????????????? ??????, ??????????????? – ??? ?? ??????? ????????????? ?????. ???????? ?? ?????????? ?????????? ??????, ??????????? ? ???????? ?????? ?????????? ? ??????? ?? ??????????, ??????????? ?????? ? ?????????? ??????? ? ?????????, ??????????????? ?? ????????? ??????.
Cryptocasino reviews https://crypto-casinos-canada.com in Canada – If you’re looking for fast BTC/ETH transactions and clear terms, cryptocasino reviews will help you evaluate which platforms offer transparent bonuses and consistent payouts.
BankID-fria kasinon https://casinos-utan-bankid.com Manga spelare forbiser hur mycket uttagsgranser och verifieringskrav varierar, men BankID-fria kasinon hjalper dig att jamfora bonusar, betalningsmetoder och tillforlitlighet.
Casinos, die Paysafecard https://paysefcard-casino-de.info akzeptieren: Viele Spieler in Deutschland mochten ihr Konto aufladen, ohne ihre Bankdaten anzugeben. Casinos, die Paysafecard akzeptieren, ermoglichen sichere Prepaid-Einzahlungen mit einem festen Guthaben. So behalten Sie die volle Kontrolle uber Ihre Ausgaben und konnen weiterhin Spielautomaten und Live-Dealer-Spiele spielen.
???????? ? ?????????? ????? ?? ????? ????????: ????????? ??????, ?????????????? ????? ?????, ????????????, ??????????, ???????????? ????????? ? ?????????. ?????????????? ??????, ??????????? ?????? ? ???????? ????????. ??????????????? ? ?????????.
?????????? ???????? ???????????? ?????? – ??? ???????? ?????????????? ??????, ????????????? ?????? ??? ????????? ????????? ? ???????????? ? ????????. ???? ???????? ?????? ??? ????????????? ???????, ??? ??????? ?????? ?? ???????? ?????? ?????? ??? ????????????? ???????????. ????, ????, ??????? ?????? ????? – ???????????? ?????? ? ?????? ???????? ????? ?????????, ??????????? ???????? ?????? ???????????? ????????????, ???????? ? ?????? ????????. ??? ?????????? ? ????????????? ? ???????????.
???????? ????????, ?????? ???????? ?????????? ?????????? ??????, ??????????
https://git.sskuaixiu.com/callummclaughl
?????????? ?????????? ??????? ?????? — ????? ?????
https://gitea.madf12.com/ashleighdemain
Updates on the Topic: https://tomenfantphare.fr
New releases are here: http://www.rivierapokerclub.fr
bukmacher internetowy mostbet pl oferuje szeroki wybor zakladow sportowych, zakladow na zywo i slotow od czolowych dostawcow. Oferuje szybka rejestracje, bonusy dla nowych graczy, przyjazna dla uzytkownika aplikacje mobilna, natychmiastowe wyplaty i calodobowa obsluge klienta.
Things Worth Watching: https://www.trimartolod.fr
https://infolenta.com.ua/obov-iazky-cherhovoho-kpp-povnyy-spysok-ta-pravyla-vykonannia-sluzhbovykh-funktsiy/
bukmacher internetowy mostbet casino oferuje szeroki wybor zakladow sportowych, zakladow na zywo i slotow od czolowych dostawcow. Oferuje szybka rejestracje, bonusy dla nowych graczy, przyjazna dla uzytkownika aplikacje mobilna, natychmiastowe wyplaty i calodobowa obsluge klienta.
Today’s Focus: https://www.opencart-france.com
More details One click: http://www.rando-cretes.fr
Only top materials: https://chuyenhangphap.fr
?????? ?? ????? — ?????????? ?????????? ?????? ?????? ??? ????????
https://hifzcollages.harkcreation.com/author/anitrasecombe/
??????? ?????? ?????? — ??????, ???? ?????????
https://lagosproperty.net/author/florenemoreton
?????????? ???? ?????? ?? ??????? ????, ????????? ? ???????
https://miurl.do/adell12c433750
?????????? ?????? ?????? — ??? ?? ?????? ??????
https://pagemelon.com/damiensige
????? ?????? ? ??????????? ?????? ?????? ??? ????????? ???????? ? ???? ???????? https://mti5.me/ ? ????????? ??????? ? ????? ???????. ?????? ? ???????????! ????????, ????????? ? ?????? ??????, ?????? ?? ???????? ? ????????? ?? ??????????? ? ?????????? ??????? ? ???? 90 ???? ??? ????????????? ?????????! ??????? ??? ???? ????? ????????????? ?? ?????.
????????????? ????????? ??? ?????????? ????????? ???????? ????????? ???????? ??????, ?????????? ????????????? ????????? ? ???????????? digital-???????????. ?????????? https://digital.econ.msu.ru/ ???????? ??????????? ???????? ? ?????????????? ??????????? ?? ???????? ???? ??????, ??? ?????? ??????? ??????????????.
?????????? ?????????? ?????? ?????? ??? ????
https://quenly.com/@rogersimonetti
?????????? ????? ?????? ????? ???????? ???????
https://shrtlnk.ink/carrispargo76
????? ?????????? ?????? ? ??????? ?????????? ????? ?? ????????????, ??? ???????? ???????????, ????????? ?????????? 1Win ???????????? ? ??????????? ?????????? ??? ???????? ?????????????. ?? ?????? https://t.me/s/win1win_skachat_na_android ????? ??????? ??????????? ?????? 1win ??? Android ? ???????? ? ??????? ?????? ?????????? ???????????? ?????????: ?? ????? ? ????-?????? ?? ??????? ???????? ? ??????? ????????. ??????? ?????????, ?????????????? ??? ?????????, ??????? ?????? ? ??????????? ??????? ?? ????????? ? ????? ????? ?????? ?????????? ???????? ??????? ??? ???, ??? ????? ????????, ???????? ? ??????? ? ???? ??????-??????.
?????????? ?????????? ? ??????????? ?????? ?????? ?? ???
https://tigerlink.me/marklaidlaw270
????? ????? ???????? ??? ? ?????????? ???????????, «???????????????» ? ??????? — ??????? ????? ??? ????????? ? ???????????: ?????????, ????????????, ???????, ??????, ?????????, ????????? ? ??? ?? ??????, ??????? ????, ???????? ? ??????. ???????? — ??????????? ????????????? «???????-?????????» ? ????? «??? ????», ???????????? ? ??? ??????????????? ?? ????, ? ??????? ????? ???????? ???????? ?????????? ????????????. ????????? ?? https://www.svartk.ru/ — ?????? ??????? ???????, ??????? ?????????????? ? ???????? ????? ? ????????????? ?????????.
Straight to the best here: https://evendis.fr
????????? ? ???? ????: https://efaflex.ru
https://qwertyoop.com qwertyoop
?????????? ????? ?????? ????? ?????????? ?? ????????
https://video.office.saltworks.pl/@bertiewindsor?page=about
?????????? ?????????? ??????????? ?????? — ??? ?????
https://www.cinnamongrouplimited.co.uk/agent/wilmer52y81577/
???????? ???????????? ?????? ???????? ???? http://kupit-kursovuyu-24.ru .
anal sex for gays anal sex for gays .
?????? ??????????? ??????? ?????? — ???????? ??????? ? ?????
https://www.travelmapsgo.com/andreshansford
??????? ????? ???????? ???????? ?????? http://www.kupit-kursovuyu-26.ru .
????????? ???????? ?????? ?? ????? ???? kupit-kursovuyu-21.ru .
???? ???????? ?????? http://www.kupit-kursovuyu-23.ru .
??????? ?????? https://forthenaturalwoman.com ? ?????, ??????? ? ???????????: ????, ???? ?? ?????, ????????, ?????????, ??????? ? ?????? ???????. ???????? ??????, ??????? ??????, ?????? ????????? ? ??????? ???????? ??????. ??????????????? ? ?????????? ? ???????? ???? ??? ???? ?????? ????.
??????? ??????? https://mynewsmonitor.com ??????: ????? ?????? ??????? ??? ? ?????? ? ???????? ???????. ????????, ?????????, ????????, ???, ????? ? ????????. ??????? ??????, ??????????? ??????, ?????? ????????? ? ??????? ?????, ??????? ??????????? ? ?????? ????????? ???????.
?????????? ? ??????? https://allnews.in.ua ???????: ???????? ??????? ? ??????? ???????? ? ??????????? ????????????? ?????????. ???????? ??????, ??? ?????????, ?????? ??? ????? ? ? ???? ????? ????????. ????? ??????????? ? ??????? ???, ????? ?? ?? ???????? ?????? ?????????.
??????? ??????? https://newsline.in.ua ??????: ?? ??????? ????????? ?? ???????? ??????? ? ?????????? ????????????. ????????, ?????????, ????????????, ?????????? ? ????????. ?????? ??????????? ????? ? ??????? ?????, ????? ?????? ??????????????? ?? ????, ??? ??????????.
?????????? ?????? ?????? ?? ?????? ??????????? ??????????
https://devkona.net/katherinaserle/katherina2006/wiki/tamozhennoe-oformlenie+10I.-
oficjalny mostbet mostbet casino
?????????? ?????????? ??????????? ?????? ??? ????????
https://git.barneo-tech.com/deannepfeiffer
??? ??????? https://ua-news.com.ua ??????? ? ????? ??????: ?????????? ???????, ?????? ???????, ????????, ?????? ? ?????????. ???????? ??????, ??? ????? ?? ???????????, ??? ??????? ??????? ????? ????? ? ?????? ??? ???????. ?????????? ? ?????? ????????? ???????.
??????? ??????? https://ukrnews.in.ua ???????: ????????, ?????????, ????????????? ???????, ?????, ???????? ? ???????????? ????. ??????????? ??????, ?????? ? ????????? ??????. ?????? ??????? ???, ????????? ? ????? ????? ??? ???????? ? ???????? ??????.
????????? ?????? https://ua-today.com.ua ? ???????? ?? ?????????????: ?????? ??????????? ?????????, ?????, ??????????? ????????? ? ???????? ?????????. ??????? ????? ???????, ??????? ?? ?????, ????? ?????????? ? ??????? ?????? ? ???????? ?? ????.
??????????? ???? https://cargurus.com.ua ??????: ?????? ???????, ????????, ?????? ????? ? ??????????? ???????????, ????-??????, ?????? ?? ???????????? ? ???????????. ??????? ????? ?? ?????? ? ???????, ????????, ???????? ? ???????? ????????? ??? ????????????? ?????? ??????.
?????????? ??????? ?????? ?????? ?? ??????
https://git.nagee.dev/barneyschwab5
???????? ??? ????? ???????? ??? ????? .
?????????? ??????? ?????? ?????? ????????, ??????? ???????
https://gitea.biutag.com/calebolney2140
?????? ???????? http://www.kupit-kursovuyu-26.ru .
????? ????????????? ? ??????????? ?????? ????????? ???????????????? ???????? ???? ?????? https://www.vesper.ru/ – ?? ???????????? ??????? ????????? ???????????????? ? 1992 ????. ? ??? ??????? ??????? ? ???????? ?? ??????. ???????????? ? ????? ?????????? ? ????????, ???????????? ???? ?? ????? ?????????.
?????? ???? https://autoindustriya.com.ua ??????: ??? ?? ??????????? ? ?????????. ?????? ? ????????? ???????, ????-??????, ???????? ?? ??????? ? ????????????, ?????????? ? ???????? ? ???????, ??????? ?????. ???????? ??????? ??????, ?????? ???????? ???????? ? ?????????? ?? ??????????.
??????????? ??????? https://womanstyle.com.ua ?????? ??? ???, ??? ????? ???????? ???: ????? ? ???????, ?????????? ? ?????????, ???????????, ???, ??????????? ? ??????. ?????????? ????????, ???-?????, ???????? ? ????????????? ?????????, ??????? ???????? ?????????? ? ???? ? ???? ? ???????.
??????? ?????? https://womanblog.com.ua ? ??????????? ??????: ?????? ???? ? ???????, ????????, ??????, ???????, ???????????? ? ????????????? ???????. ?????????? ??????????, ???????????? ???????????? ? ???????? ???? ??? ???????????? ?????, ??????? ? ??????? ???????.
??????????? ????????? https://arguments.com.ua ??????: ??????? ??????? ???, ?????????? ?????????, ?????? ????????? ? ????????? ? ???? ???????. ????? ? ???????? ???????, ???????????? ???????, ???? ? ?????. ???????? ??????????? ? ???, ??? ?????????? ? ?????? ? ????.
https://aviator-game.biz
????????? ??????? ????? http://www.kupit-kursovuyu-21.ru/ .
?????????? ??????? ?????? — ????? ? ?? ??????
https://gitlab.liruwei.cn/sallyi16111950
???????? ?????? ?????? ?????? http://www.kupit-kursovuyu-23.ru .
aviator betting game
???????? https://accs-shop.com/ – ??? ??????? ????????? ?1 ? ??????????? ?????? ??????, ? ??????? ?? ??????? ?????? ???????? ? ??????? ????????????. ?????????? ????????? – ??? ?? ??????????? ??????? ??? ???? ??????????? ?????. ?????? ??????? ???????? ?????????? ???????? ????? ????????, ?? ?????? ???? ??????? ? ????????, ? ????????? ???????? ??????!
aviator game official site verified
pobierz kasyno mostbet mostbet
???? ?????? https://automotive-news.com.ua ??? ???, ??? ????? ????????????: ??????? ?????????, ?????? ?????, ????-??????, ?????? ?? ?????? ? ????????????, ????????? ??????? ? ?????? ???? ?? ??????????. ????, ?????, ?????? ????????? ? ???????? ?????? ?????????? ? ????? ?????.
?????????? ?????????? ?????? ?????? — ??????? ??????, ??? ??
https://jaipurnest.com/author/cindahelm85522/
???????????? ?????? https://garden-story.com ??? ?????????????? ? ??????? ????????: ?????? ? ?????????? ?? ???????, ??????? ? ?????????????, ?????? ?????????? ? ????????????, ????????????, ?????, ????-??????? ? ?????? ?????????. ???, ????? ???????? ???????????? ? ????????? ??????.
?????? ? ??????? https://remont-sam.com ? ?????????????: ?? ?????????? ??????? ? ????? ?? ??????? ? ??????. ????????? ??????????, ?????? ????????????, ???????? ??????????, ????-??????? ? ????????. ??????? ????????? ?? ????? ???????? ?????? ????? ?????? ??????? ??? ?????? ???????.
????? ????????? ?????? ???? ??????? Terapiazvu.com ?????????? ???????? ?????-????????????? ??????? ?????????? ??????? ?????? ?????? ?????? ? ??????????? ??????? ??????????-???????????? ???????. ???????????????? ??????? ???????? ??????????????? ???????? ??????? ?????? ? ??????? ??????, ???????? ????????? ?????????????? ?????????? ???? ???????? ?? ?????????? ? ???????????? ?????????? ???????? ?? ??????. ?????? ? ??????? ?????? ????????????? ????????? ??????????, ??????????? ?????????????? ????????? ???????? ? ???????????? ?????????? ?? ??????????????? ?????????.
??? ????? ???????? ???????? https://www.kupit-kursovuyu-22.ru .
?????????? ?????????? ?????? ?????? — ????? ?????? ????
https://majlis.sharechanneltv.com/@jaxonparis6608?page=about
porn online porn online .
Game-Lands https://game-lands.ru/ – ??? ???? ? ?????????? ??????? ? ????????????? ??? ???????? ? ??????? ???????. ????? ?? ??????? ?????? ??????, ??????? ????? ? ??????, ?????? ???????????? ?????????, ????????, ????????, ? ??????????? ????? ?? ???????. ???????, ??? ???????? ?????? ??????????, ??? ?????? ? ??????? ???????? ? ? ???? ?????? ? ????? ?????. ???, ????? ???????? ????? ? ???????? ??? ??????????? ??????? ???????.
?????????? ?????????? ??????????? ?????? — ??? ????????
https://nhadatdaibang.com/estate_agent/magdarosser51/
?????????? ????? ???????????? ?????? ??????????? ???????? ??????, ???????? ???????????? ??????????? ? ?????? ??? ?? ????? ???????? ???. ?????? Audiomap.ru ?????? ?????? ?????????? ????????? ????????? ?????? — ?? ?????????????? ??????? ?? ?????????? ? ????????????????. ??????? ????????? ?? ????????? ???????? ?????? ????? ???????????? ?? ????: ???????? ??????, ?????, ?????????????? ?????????? ??? ??????????????? ??????????. ???????? ?? https://audiomap.ru/ ? ????????? ?????????? ?????????? ????? ?????? ??? ??????????? ? ?????????? — ?????????? ??????? ???????????? ? ?????? ?????? ??????????????? ? ????????.
?????? ???????? ?????? ?????? ???????? ?????? .
?????? ???????? https://kupit-kursovuyu-26.ru .
Right now it looks like BlogEngine is the top blogging platform out there right now. (from what I’ve read) Is that what you’re using on your blog?
juegos friv gratis
?????????? ????????????? ?????? ??????? ????? ???? ????
https://properties.trugotech.com/author/rosalyn4934182/
???????? ??? ????? https://kupit-kursovuyu-21.ru .
?????????? ?????????? ??????????? ?????? — ??? ?????
https://rubpal.com/@cyrusclaxton96
????????? ?????? ?? ????? https://kupit-kursovuyu-23.ru .
XXX-Video mit gro?em Arsch XXX-Video mit gro?em Arsch .
?????????? ??????? ?????? — ?????, ??????, ????????
https://superocho.org/@miqueljansen1?page=about
????? ???????? ????? ?? ????????? ?????? seoprofi.org ???????????????? ?? ?????????? ???????? ?????????? ??? Rutube ? VK ?????, ? ????? ?????????? ???????????? ?????? ? ??????? ?????? ???????. ??????? ??????????? ??????????? ?????????? ?????? ? ?????????? ?????????? ? ????????? 40-80%, ??????????? ??????????? ?????????? ? ???????????????? ????? ? ????????? ???????????? ??? ?????? ???????. ?????? ???????? ?? 1200 ?????? ?? 1000 ?????? ???????, ?????? ???????? ?????????? ? ??????? 1-3 ????? ? ?????????????? ?????????? ????????.
?????????? ????????????? ?????? ??????? ????? ???? ????
https://upropertyz.com/author/coryw818819892/
???????? ???????????? ?????? kupit-kursovuyu-22.ru .
???????? ???????????? ???????? ???????? ???????????? ???????? .
??????? ????? ???????? ???????? ?????? http://www.kupit-kursovuyu-26.ru .
???????? ??????????? — ?????????? ?????????? ? ??????????? ?????? ??? ????????
https://wishi-washi.com/author/vtffernando843/
???????????? ?????? https://sovetremont.com ? ????????????? ????????: ?????? ???????, ????????????? ?????, ?????????? ???????, ???????, ??????, ?????? ? ???????????????. ???????????, ?????, ??????? ? ???????????? ?????????, ??????? ???????? ????????? ????? ? ??????.
porn games porn games .
?????? ? ????????????? https://stroyline.com ? ???????: ????????? ??????????, ?????? ??????????, ????????????, ???? ?????????? ? ???????, ?????? ???????? ? ???????? ???????. ???????? ???????????? ??????, ???????? ???????? ?????? ? ?????????? ????? ? ??????.
??????-?????? https://stroyinfo.com ? ????????????? ? ??????? ??? ?????????? ???????, ????? ? ???: ???????? ??????, ?????, ???-?????, ?????? ?????????? ? ???????, ?????? ?? ??????? ? ?????????? ????????. ???, ????? ??????? ?????? ?????? ?????? ??? ???????? ?????????????? ???????????.
?????? ??????? https://ukrportal.com.ua ??????? ? ????: ????????, ?????????, ????????, ????????????, ????????? ? ????????? ?????????. ??????????? ?????????? 24/7, ??????????? ????? ? ??????????? ??????. ??????? ?? ????????? ?????????, ??????? ????????? ??????? ?????? ? ????? ????.
????????? ??????? ???? – ??? ?????? ?????????, ???????? ??? ? ???????? ?????, ??? ???????? ??????? ?????????? ???????????? ????. ????? ????????? ???????????????? ?? ???????????? ???????? ????? ????? «?????????», ?????????? ????????? ?????????? ? ???????????? ?????? ? ??????? ????. ???????? ???? ?????? ?????????????, ?????? ?????????? ????????? ? ????? ?????? ?????, ? ???????????? ??????? ????????? ????????? ??????? ??? ??????? ?????? ??????. ? ??????????? ????????-???????? https://prometall.shop/ ???????????? ???? ? ?????, ???????? ????????? ? ??????????????? ????????, ? ????? ???????????? ???? ??? ????: «?????», «???????», «????? PRO». ???????? ?????????? ?????? ???????? ????? – ?? ???????????????? ???????????? ?? ???????? ?? ?????? ? ????????? ??? ????, ????? ????? ? ??????????? ???? ????????? ? ????????.
??????????????? ??????????????? ????? ? ??????? ?????? ? ?????? ???????????? ???????????? ???????? ??????????? ?????? ?? ?????????? ????????? ??? ?????????? ???? ????????? ? ????????????. ??????????? ???????? ???????? ?????? ????, ?????????? ? ??????? ????????? ??????????????? ????????????? ? ??????? ?????? ??????. ????????? ?????????? ? ?????????? ???????????? ?? ????? https://www.ctgroup.kz/ ??????? ????????? ?????????? ???????????? ????? ???????????? ?? 6 ???????? ? ???????????? ??????? ? ????????????? ??????? ? ???????????? ????????????? ?? ????????? ???????? ?????.
?????????? ?????????? ?????? ?????? — ??? ??? ????, ?????? ?? ?????
https://www.pakproperty.ca/author/tanyab19212959/
???????? ???????? ?? ????? http://www.kupit-kursovuyu-21.ru .
???????? ? ???????? ??????? ?????? ?????? https://behruzoglu.com/ru/ – ??????? ????????????? ???????? ? ?????, ??????? ?????? ???. ???? ??? ????? ????????????????? ??????? ???? ???????? ? ???, ?? ????? ?????? ???????????. ??? ??????????????? ???????? ? ????????, ?????? ???????? ??????? ?????????, ??? ???????? ????????. ?????? ?????? – ????????? ??????? ???? ???????? ? ?????. ?????, ??? ????????? ????????????? ???????? ? ??? ??? ??????????????? ???????? ? ?????? ??? ???????? ??????? ???? ???????? ? ???????? ???? ???.
?????? ????????? ??????????? https://www.kupit-kursovuyu-23.ru .
??????????? ??????????? ???????????, ?????????? ?????????? ??????????? ??????
https://credicasaonline.com/agents/jeelisette892/
https://long-living.ru/
?????????? ??????? https://ukrmedia24.com.ua ??????? ? ???? ? ????? ?????: ??????? ??????? ???, ??????, ??????????? ?????????, ????????? ? ???????????? ?????????. ????????, ?????????, ??????????, ???????? ? ?????. ??????, ?????????? ? ?????? ??? ??????????? ??????.
??????? ??????? https://ukrinfo24.com.ua ? ????: ??????????? ??????????, ?????? ???????? ???????, ????????, ????????? ? ?????????. ?????? ??????????? ????????? ? ??????????? ??????. ?????? ? ????? ????, ??? ?????????? ? ?????? ? ?? ????????????? ????? ????? ??????.
????? ???????? https://uavesti.com.ua ??????? ? ????: ????? ?????? ??????? ???, ?????????? ????, ?????????? ?????? ? ???????? ?????????. ??????? ??????, ??????? ??????????, ??????????? ??????. ????????, ????????, ?????????, ???????? ? ??????? ????????? — ??? ?? ????? ?????????.
??? ??????? https://uanews24.com.ua ??????? ? ???? — ??????, ?????????? ? ???????: ??????? ? ????????, ?????????, ?????, ???????? ? ??????. ????????? ??????, ???????? ? ????????? ???????? ??????? ?????? ??????? ?????????????. ?????????? ?????????? ? ??????? ?????????.
??????? ???????? ?????? ????????? ? ??? ??????????? ?? ?????? ??????????, ??? ??????? ??? ????? ??????? ???????? ?????? ???????? ??? ???????????? ?????? ????????! ?????? ???? – ??? ??? ? ???????? ???????? ??? ?????? ????????????? ???????????. ????????? ???? ????????? ? ??? ?????? ? ???????? ???? ???????!
?????????? ?????????? ? ??????????? ?????? — ?????
https://funnyutube.com/@christyburrowe?page=about
vingfoil ????? ???? ???????
?????? ????????? ? ?????????? http://www.kupit-kursovuyu-22.ru .
????? ?????????? ????????? ??? ?????????? ?? Windows? ???????? https://pcutilites.com/ – ?? ??????? ??????? ??????? ???????? ? ?????????? ????????? ???? ????????? ???????? ??? ????????? Windows. ???????? ? ??????? – ??? ??? ????????? ??? ???????, ????, ?????, ??? ??????????? ? ???????. ????? ? ??? ???? ?????? ? ????????? ????????, ? ????? ?? ????????. ????????? ?? ?????.
??????? ?????? ?????? — ??????, ???? ?????????
https://git.kitti.ac.th/meredithamess
???? ??? ?????? https://golosiyiv.kiev.ua ??????? ????? ???? ? ???? ?????: ???????? ?????? ? ???? ? ?????, ??????????, ?????, ??????????, ?????? ? ?????. ???????? ????, ?????, ???-????? ? ????????????? ???????. ???????? ???????? ?????? ????? ??????? ? ?????? ? ??????? ? ????.
??????-???? https://funtura.com.ua ??? ?????? ?????? ????????: ?????? ???? ? ???????, ???????? ????? ?????, ???????, ??????, ????????? ? ????????????. ?????????? ??????????, ?????? ????????? ? ????????????? ?????????, ??????? ???????? ??????????? ???? ????????? ?????? ????.
???? ??? ?????? https://e-times.com.ua ? ?????, ??????? ? ???????????: ????, ??????, ???? ?? ?????, ????????, ?????????, ????? ? ???????. ?????????? ??????, ??????, ???-????? ? ?????? ???????. ???????? ?????????? ? ????, ??????????? ? ???????? ????? ???? ?????? ????.
?????? ??????? https://womenclub.kr.ua ?????? ??? ??????? ? ?????? ?????? ????????: ?????? ??? ??????? ? ????, ?????????, ?????, ?????, ??????? ? ?????. ??????? ????????? ?? ????????, ???????? ??????, ????? ? ????????, ??????? ???????? ???????? ?????? ?? ?????? ???????.
Mi ar?yorsunuz casino hos geldin bonusu? Sekabet Casino’ya Türkiye’den güvenle ula?mak, üyelik ve finans i?lemleri rehberini görmek ve en iyi geli?tiricilerin oyunlar? ile spor bahislerini incelemek için villaperret26.com adresine göz at?n. Promosyonlar?m?z ile bonuslar?m?z, kullan?c?lar için yüksek de?erli ödül sistemi sunar. Mobil uygulamam?zla diledi?iniz yerde oynay?n — basit arayüz, tüm cihazlara h?zl? kurulum.
??????????? ?? ????? — ?????????? ?????????? ??????????? ?????? ?????
https://git.valami.giize.com/taylorf5991451
?????? ? ???????? https://zoo-park.com ????? ??????? ? ???????? ???????. ?????????????? ?????????, ???????????, ?????? ????, ???????, ???????? ? ????????????? ??????????. ???????? ????? ?? ?????, ?????? ??????? ? ??????????? ??????? ? ?????????.
?????? ? ???????? https://myzoofriend.com ?????? ?? ????? ?? ?????????, ????????, ???????, ?????????? ? ?????????. ?????? ?????? ? ???????????, ???????????? ???????????, ??????? ???????? ? ?????????? ????? ? ??????, ??????? ? ????? ???????.
???? ?????? https://just-forum.com ? ?????? ??????? ????????: ???????, ??????, ?????, ??????????? ????, ?????? ?? ???????, ???????????? ? ??????? ??????????. ??????? ?????? ?????????, ???????? ??????, ???????? ?????? ??????? ? ??????? ????????? ?? ?????? ? ???????.
????????? ?????? https://infonews.com.ua ? ?????? ??????? ???????: ??????????? ?????, ??????? ??????, ???????? ? ?????????. ????????, ?????????, ????????, ??????????, ???????? ? ?????. ?????????? ? ?????? ????????? ??????? ? ??????? ????????? ???????? ??? ??????????? ??????.
?????????? ????????????? ?????? ????? ??? ???????
https://gitea.quiztimes.nl/marjorieconawa
?????? ?????? ?????? ?????? ?? ????? Telegram – ??? ???????? ??????????? ??????? ?????????? ????????, ?????????? ??? ?????????????? ?????. ? Telegram ????? ????? ???????? ? ???????, ???????????? ???????????? ?????? ?? ?????????????? ????????. ????? ?????????? Telegram ?? ?????, ??????? ? ?????????????? ????????? ??? ????, ???????? ????????????? ? ???? – ??? ??? ???????? ????????? ?????? ?? ????? ? Telegram. ???????? Telegram, ??????? Telegram, ???????? Telegram – ???????? ???????? ????? ????? ? ??????? ?????? ?? ?????!
https://kitehurghada.ru/ ???? ????? ???????
ETNA https://www.etnasoft.com/ is a white-label fintech platform for broker-dealers and RIAs offering integrated trading, wealth management, and back-office solutions. Features include multi-asset trading, automated portfolio rebalancing, compliance automation, mobile apps, and 20+ custodian integrations. The platform deploys in two weeks, supports complete brand customization, and scales from startups to established firms managing billions in assets.
??????? ???? ????????????? ? ??????? ???? – ? ??? ??? ???????? ??????, ????? ?????????, ?????????? – ??????? ??????? ?????????????. ????????????????, ??????, ??????????, ??? – ???????, ?????????? ???.
?????????? ?????????? ?????? ?????? — ?????
https://hubenar.com/albakendall171
https://opalubka.market/ opalubka market
?????? ? ???? https://sovetyogorod.com ???? ? ???????: ?????? ? ????? ?? ????? ?? ??????, ???????, ???????, ????????????? ? ?????? ? ????????? ????????. ?????? ????????????, ???? ??? ?????? ? ???????????, ??????????? ??????? ? ???????? ?????? ??? ??????.
??????? ?????? https://dreamywoman.com ? ????? ?????: ??????? ? ????, ????, ????????, ??????????, ?????????, ????? ? ???????. ???????? ??????, ????????, ???-????? ? ????????????? ???????. ???, ????? ?????????? ? ????, ??????????? ? ???????? ???? ?? ?????? ????.
??????????? ??????? https://nova-woman.com ???? ??? ??????? ? ??????: ?????? ???? ? ???????, ???????, ??????, ????????????? ????????, ????????? ? ????????????. ???????? ??????, ??????, ????? ? ????????, ??????? ???????? ??????????? ???? ????????? ? ??????????.
????????? ?????? https://ua24news.com.ua ???????: ??????????? ??????? ???, ????????, ?????????, ????????, ???????????? ? ????????????? ????????. ??????????? ?????, ?????????, ???????? ? ?????????. ????????? ??????? ? ????? ?????? ? ???? ? ??????? ??????? 24/7.
???? xrumer ???? Xrumer 19: ???? Xrumer 19 — ??? ????, ??????????????? ??? ????????????? ? ????? ?????? ??????? Xrumer – ??????? 19.
?????????? ???? ?????? — ?????? ? ?? ?????????? ????
https://lidmilink.ru/wilson73128433
??????????? ???????? «???????????» ?????????? ?????? ???? ???????????? ?????-???? ? ????? ??????????? ??????? ??? ??????? ?? ?????? ? ????????. ????? ? 10-?????? ????????? ????????? ?????? ????????? ?????????: ?? ?????????? 3D-??????? ?? ?????? ????????? ???????. ????????? ? ???????????? ? ?????? ???????? ????? ?????? ?? https://press-forma.by/ – ????? ???????????? ??????? ?????, ??????? ??????? ???? ? ??????? ??????????????. ????????? ???????? ??????????????? ?????????? ? ????, ?????????? ??????????? ? ??????? ? 2-3 ???? ?????? ???????????? ???????????? ? ?????.
???????? ???????? ?????? ??????????? http://kupit-kursovuyu-22.ru/ .
??????? ???????? ?????? ????????? ? ??? ??????????? ?? 5000 ???? ?????? ?????? ? ?????? ? ????????????? ? ??? ?????? ??????? ????? ??? ????? ????? ???????? ???????? ?? ???????? ??????. ??? ?? ?????? ??????, ? ????????? ??????????? ??????? ????????? ????????, ??????? ???????? ?????? ?? ??? ??????? ????. ??????? ??????? ??????? ??? ???????? ???????????? ?????? ? ????? ?????, ??? ??? ???? ??????? ????, ??????? ??????? ? ???????? ??????. ?? ??????? ????? ?? ?????? – ?????????? ??????????? ?????????????!
?????????? ?????????? ? ??????? ?????? ??????? ?? ?????
https://musiccosign.com/christoperprof
??????? ??????? https://smi24.com.ua ??????? ? ????? ?????: ?????????? ???????, ?????? ??????????, ?????????????, ????????? ? ???????????? ?????????. ??? ????????? ?????? ???????? ????????, ??? ?????????? ? ?????? ? ??? ??????? ?????? ?? ????? ?????.
??????-????????? https://novosti24online.com.ua ?????? ???????: ????? ????????, ????????? ???????, ????????, ?????? ? ?????????. ????????, ?????????? ???????, ?????????, ????????????? ??????? — ??? ??????????, ?????????? ? ??????? ??????? ????????.
????????? ?????? https://mediasfera.com.ua ??????? ??? ???, ??? ????? ???? ? ?????: ?????? ??????????, ?????? ???????? ???????, ?????????? ?????? ? ????????? ????????? ? ????????, ????????? ? ????????. ??????? ??????????, ??????? ????????? ? ??????????? ??????????.
??????? ??????? https://mediaportal.com.ua ? ??????? ???????: ????? ????????? ???????, ??????? ?? ?????, ????????? ??????? ? ?????????. ???????? ????????, ?????????, ????????????, ?????????? ??????? ? ????????????? ?????????. ?????? ??? ???, ??? ????? ???????? ?????? ??????? ???.
?????????? ?????????? ??????????? ?????? — ??? ????????
https://play.ayooka.com/@orvilleboddie1?page=about
?????????? ????????????? ?????? ?? ??????, ????????? ?? ?????
https://realtorsatish.com/author/adrianastamper/
??????? ???? https://loveliness.kyiv.ua ? ?????????? ?????????: ???? ?? ????? ? ????????, ???????? ??????, ??? ? ???, ????, ?????? ? ???????. ???????? ????????????, ?????????? ????????? ? ??????????? ??? ?????? «????». ??????? ????????? ?? ???????? ? ?????????? ??????????.
????????????? ???? https://kolesnitsa.com.ua ?????? ??? ????????? ? ??????? ??????????: ?????? ???????????, ????????? ????????????, ????-??????, ?????? ?? ?? ? ???????, ?????? ??? ? ???????????. ?????????? ???????, ????????? ????? ? ?????????, ??????? ???????? ?????? ?????????? ?????.
?????????? ????????? https://mediacentr.com.ua ?????? ? ???????? ?? ????????????? ? ?????: ?????? ???????, ????????????? ??????, ???????? ? ???????????. ???????? ????? ??????, ???????, ?????, ?????????? ? ???????????? ??????? ?????. ??? ?????? — ?? ????? ????????.
?????? ??????? https://lugor.org.ua ???? ??? ???, ??? ????? ???? ?????: ????? ?? ??????? ? ?????, ??????????????? ??????, ???? ??? ????, ?????????, ??????????? ? ????????? ????. ????????, ???-?????, ??????? ? ??????, ??????? ??????? ???????? ? ???????????? ?????.
best lifestyle hub – A nice selection of lifestyle goods, arranged clearly for easy exploration.
????? ???????? ??? ??????? ???????? ???????? ???? Zipin https://zipin.ru/ – ? ??? ? ??????? ????? 1500 ????????? ?? ??????? ?????????????? ? ?????????, ??? ????????? ??????? ???????. ?????????? ??? ??????? – ??? ?? ??????? ??? ??????????? ??? ???????. ??? ????????????? ????????? ????????????????? ?????? ? ??????? ?????????.
??????? ?????????? ?????????? ? ??????? ?????? — ?????? ? ??????
https://sondevs.com/CNZCx
????????-??????? https://cybergarden.pro/ ?????????? ??????? ????? ?????????????? ? FPV-?????? ?? ??????? ??????????????, ??????? ???????????????? ?????? DJI Mavic 3, Matrice ? Agras ??? ?????? ? ????????? ?????????. ??????? ???????? ???????????????? ?????? ??????????, FPV-??????, ?????????????? ??????? ? ???????? ???????????? ? ?????? ????????????? ???????. ??????????? ????????????? ?????????? ???????????? ?????????????, ????????? ????????? ?? ???????? ? ??????? ??????????????? ??????? ? ????????? ???????.
your shopping corner – Wide selection of items, browsing feels smooth and easy today.
Neat Click Hub – Clean and structured interface with easy-to-follow sections.
??????? ???? https://loveliness.kyiv.ua ? ?????????? ?????????: ???? ?? ????? ? ????????, ???????? ??????, ??? ? ???, ????, ?????? ? ???????. ???????? ????????????, ?????????? ????????? ? ??????????? ??? ?????? «????». ??????? ????????? ?? ???????? ? ?????????? ??????????.
????????????? ???? https://kolesnitsa.com.ua ?????? ??? ????????? ? ??????? ??????????: ?????? ???????????, ????????? ????????????, ????-??????, ?????? ?? ?? ? ???????, ?????? ??? ? ???????????. ?????????? ???????, ????????? ????? ? ?????????, ??????? ???????? ?????? ?????????? ?????.
?????? ??????? https://lugor.org.ua ???? ??? ???, ??? ????? ???? ?????: ????? ?? ??????? ? ?????, ??????????????? ??????, ???? ??? ????, ?????????, ??????????? ? ????????? ????. ????????, ???-?????, ??????? ? ??????, ??????? ??????? ???????? ? ???????????? ?????.
?????????? ????????? https://mediacentr.com.ua ?????? ? ???????? ?? ????????????? ? ?????: ?????? ???????, ????????????? ??????, ???????? ? ???????????. ???????? ????? ??????, ???????, ?????, ?????????? ? ???????????? ??????? ?????. ??? ?????? — ?? ????? ????????.
Global Ethical Essentials – Products thoughtfully arranged, browsing feels seamless and intuitive.
daily picks shopping zone – Items are well organized, exploring the site feels quick and natural.
?????????? ?????????? ?????? ?????? — ??????? ??????, ??? ??
https://tonevideos.com/@tyrellrubinste?page=about
Artful Design Hub – Thoughtful product arrangement, smooth navigation, and very easy to browse.
Conscious Picks Hub – Wide selection of ethical items, navigation is easy and pleasant.
fashion corner picks – Selections look trendy, browsing feels comfortable and effortless.
Timeless Goods Marketplace – Elegant timeless items, exploring the site is smooth and pleasant.
trend collection deals – Attractive products are arranged neatly, site feels pleasant to explore.
?????????? ?????????? ??????? ?????? — ????? ?????????
https://viewtube.in/@claudiastallwo?page=about
Modern Inspired Hub – High-quality modern items, browsing is smooth and very enjoyable.
corner for trends – Products appear attractive, browsing feels smooth and convenient.
???? ???????? Xrumer ???????? xrumer ???? ????????: xrumer ???? ???????? – ??? ?????????? ??? ?????????? ???-?????, ???????????? ???????????? ??????????? Xrumer, ? ????????? Telegram.
Visita https://juegosdetragamonedas.me/ y encontraras las mejores tragamonedas gratis de Latinoamerica. Ofrecemos una amplia seleccion de juegos de proveedores internacionales, ademas de diversos bonos y giros gratis por registrarte. Disponemos de una practica version movil. Depositos y retiros son faciles.
Future Hub Marketplace – Thoughtful assortment, website layout makes shopping seamless.
?????????? ?????????? ?????? ?????? — ?????, ??????, ??? ?????? ????????
https://www.immobiliaremercuri.it/agents/tameladrescher/
APS Trend Picks – Cozy autumn pieces stand out, and the browsing flow feels smooth throughout.
https://cap-games.jp/ ????????SEKIRO?DARK SOULS?FINAL FANTASY?Bloodborne ??????????????????????????????????????????????
Home & Lifestyle Picks – Well-curated essentials, browsing feels easy and enjoyable.
Value Corner Global – Lots of appealing finds available, and navigation stays fast and tidy.
?????????? ?????????? ?????? — ?????? ????????????? ??????
https://youtube.mitiosys.org/@alonzoy666058?page=about
Value & Premium Finds – High-quality affordable products, ordering process fast and hassle-free.
Global Value Picks – Picks look curated and neat, and the interface reacts quickly.
Curated Lifestyle Hub – Product variety is excellent, browsing is simple and enjoyable overall.
inspiration hub – Love the creative vibes here, and pages load quickly without hassle.
????????? ?????? https://infosmi.com.ua ???????: ??????? ??????? ???, ??????????? ?????, ????????? ? ?????? ?????????. ????????, ?????????, ????????, ????? ? ????????????? ???????. ?????? ??????, ??????? ????????? ???????? ? ?????????? ?????????? ? ?????? 24/7.
?????? ????????? https://expressnews.com.ua ?????? ??? ???, ??? ????? ???? ? ?????: ?????? ???????, ??????, ??????????? ? ????????? ?????????. ????????, ??????, ????????, ?????, ???????? ? ????? — ??? ? ????? ?????, ? ???????? ??????? ? ??????????? ???????????? 24/7.
?????????? ????????? https://medicalanswers.com.ua ??????: ??????? ???????, ??????????? ??????, ?????? ??????? ??????, ???????? ?? ?????? ? ????? ???????. ????, ?????, ??????????? ? ?????? ????????? ???????? ?????? ?????? ???????????? ? ??????? ? ?????? ???.
?????? ??????? ???? https://mallinaproject.com.ua ?????? ??????? ?? ??????, ???????? ??????, ???????, ??????? ?? ??????? ????????. ????????? ??????????, ??????, ???????? ???? ? ???????? ??? ?????. ??????? ??????, ?????? ?? ? ?????????? ????? ?? ????.
?????? ? ??????????? https://technocom.dp.ua ??????? IT ? ????????, ?????? ?????????? ? ?????????, ?????????, ?????, ?????????? ? ????????. ????????????? ?????????, ?????????????????, ????, ???????? ??????? ? ?????? — ??????? ?????? ? ? ??????? ??? ????????.
????? ??????? ??????????? ??????????? ??????? ? ?????????? ? ?????? ?? ???????? ????? ???????? Dreamstore https://dreamstore.by/. ????????? ? ??????? – ??? ?? ??????? ??????? ????? ???????? Apple, Samsung ? ?????? ?????, ? ????? ????????? ??????, ????????? ? ????????, ? ??? ????? ????? ??. ????????? ?? ?????.
?????????? ?????????? ?? ??????????? ????? ??????? — ??? ?? ?????? ?????????, ? ?????? ????????? ?????? ?????????? ? ????? ????. ? ????????-???????? «???????» ?? ?????? https://www.florion.ru/catalog/novogodnie-kompozicii-iz-nobilisa ???????????? ????? ??????????? ?? ????????, ??????? ????? ?? ????????? ? ????????? ?????????? ??????? ??????. ???????? ??????????? ?????? ?????? — ?? ????????? ?????, ????? ? ?????? ?? ???????????? ???????? — ???, ????? ?????????? ????????? ????????? ? ???????? ? ????? ????? ??????? ???????????? ?????? ? ????????, ????? ??? ?? ?????????? ?????.
?????????? ?????? ?????? ?? ?????? ??????????? ??????????
https://f-ast.me/floydhendon27
Handcrafted Lifestyle Hub – Beautiful artisan goods, shipping quick and packaging impressive.
Clickping Collective Hub – Well-selected products, checkout and navigation are quick and easy.
expand horizons – Excellent variety available, and the site loads quickly with no hiccups.
Ethical Picks Marketplace – Eco-friendly assortment, browsing is effortless and user-friendly.
growth beyond shop – Cool selection of one-of-a-kind pieces, with pages running smooth and clear.
????????? ?????? https://infosmi.com.ua ???????: ??????? ??????? ???, ??????????? ?????, ????????? ? ?????? ?????????. ????????, ?????????, ????????, ????? ? ????????????? ???????. ?????? ??????, ??????? ????????? ???????? ? ?????????? ?????????? ? ?????? 24/7.
?????????? ?????? ?????? ??? ???????? ????
https://git.dadunode.com/fannyspurgeon1/3983165/wiki/tamozhennoe-oformlenie+23A.-
?????? ??????? ???? https://mallinaproject.com.ua ?????? ??????? ?? ??????, ???????? ??????, ???????, ??????? ?? ??????? ????????. ????????? ??????????, ??????, ???????? ???? ? ???????? ??? ?????. ??????? ??????, ?????? ?? ? ?????????? ????? ?? ????.
?????? ? ??????????? https://technocom.dp.ua ??????? IT ? ????????, ?????? ?????????? ? ?????????, ?????????, ?????, ?????????? ? ????????. ????????????? ?????????, ?????????????????, ????, ???????? ??????? ? ?????? — ??????? ?????? ? ? ??????? ??? ????????.
?????????? ????????? https://medicalanswers.com.ua ??????: ??????? ???????, ??????????? ??????, ?????? ??????? ??????, ???????? ?? ?????? ? ????? ???????. ????, ?????, ??????????? ? ?????? ????????? ???????? ?????? ?????? ???????????? ? ??????? ? ?????? ???.
?????? ????????? https://expressnews.com.ua ?????? ??? ???, ??? ????? ???? ? ?????: ?????? ???????, ??????, ??????????? ? ????????? ?????????. ????????, ??????, ????????, ?????, ???????? ? ????? — ??? ? ????? ?????, ? ???????? ??????? ? ??????????? ???????????? 24/7.
Naturally Crafted Hub – Beautifully made natural products, browsing is smooth and very satisfying.
happy finds – The market offers plenty of joyful finds, and everything sits in a clear layout.
???????? ?????? ??????????????? ???????, ??????? ???????? ? ???????? ????????? ?????? ??????: ?????????, ????????????, ?????????????? ???????? ? ?????? ???????? ? ???????. ??? ???????? ?????? ??????? ????? ????????? ??????? ? ?????????? ?????????, ?????????????? ? ?????????? ??????????????? ? ???????? ????? ???? ? ??????? ??????. ??? ????? ???????????? ??????????? ????????, ????????? ??????????? ? ????????????. ???? ?? ???? ????????, ???????? ???????? ??? ?????? ???????? ???? ? ????????, ??????? ???????? ? ???????? – ??? ?????????? ? ????????, ???????? ? ?????????? ???????????? ?????? ???????.
??????? ?????? https://phizmat.org.ua ? ?????, ????????, ?????????? ? ???????. ?????? ???????, ??????? ?????? ???????? ? ????, ?????????? ? ???????, ???????? ??????? ? ???, ???????? ??? ?????? ? ?????? — ??? ???? ? ?????????. ??????, ?????????? ? ????? ?????? ????.
????????????? ?????? https://prostokarta.com.ua ? ???????????? ?? ?????? ? ????: ????????, ?????? ? ??????, ?????? ????????, ???? ? ????????, ????? ? ?????, ?????? ????????, ???? ??? ??????, ????????, ?????? ???? ? ?????????? ??????? ???????.
??????? ?????? https://eternaltown.com.ua ? ?????, ??????? ? ????????. ???? ? ??????, ???? ?? ????? ? ????????, ????????? ? ??????????, ??? ? ?????, ??????? ? ????????????. ???????? ??????, ????????, ???????? ? ??????????? ?????? ????.
??????? ????????? ???????: ??????????? ?????, ?????? ?? 20 ?????. ????????? ??????????? ????? ??? ? ???????, ????????, ???????? ???????????????. ???????? ?????????????, ??? ??????? ??????, ????????? ?????? ? ????? ?????.
???????? ????????? ??????? — ?????? ?? ?????? 24 ????. ????????? ???????? ? ???????????? ????, ??????????? ? ??????????. ??????????? ???????, ????????????? ?????????, ??????? ????? ?? ?????? ? ???????.
?????????? ????????????? ?????? — ?????? ???????
https://git.reacg.com/glendahorn6363
happy living corner – This corner of lifestyle finds feels inviting with clear design and smooth flow.
???????? ????????? ??????? — ?????? ?? ?????? 24 ????. ????????? ???????? ? ???????????? ????, ??????????? ? ??????????. ??????????? ???????, ????????????? ?????????, ??????? ????? ?? ?????? ? ???????.
?????????? ????????????? ?????? — ?????? ???????
https://gitea.ddegame.cn/brunocordova68
??????? ?????? https://phizmat.org.ua ? ?????, ????????, ?????????? ? ???????. ?????? ???????, ??????? ?????? ???????? ? ????, ?????????? ? ???????, ???????? ??????? ? ???, ???????? ??? ?????? ? ?????? — ??? ???? ? ?????????. ??????, ?????????? ? ????? ?????? ????.
????????????? ?????? https://prostokarta.com.ua ? ???????????? ?? ?????? ? ????: ????????, ?????? ? ??????, ?????? ????????, ???? ? ????????, ????? ? ?????, ?????? ????????, ???? ??? ??????, ????????, ?????? ???? ? ?????????? ??????? ???????.
??????? ?????? https://eternaltown.com.ua ? ?????, ??????? ? ????????. ???? ? ??????, ???? ?? ????? ? ????????, ????????? ? ??????????, ??? ? ?????, ??????? ? ????????????. ???????? ??????, ????????, ???????? ? ??????????? ?????? ????.
??????? ????????? ???????: ??????????? ?????, ?????? ?? 20 ?????. ????????? ??????????? ????? ??? ? ???????, ????????, ???????? ???????????????. ???????? ?????????????, ??? ??????? ??????, ????????? ?????? ? ????? ?????.
???????????????? ????????? ???????? ?????????? ??? ?????? ? ???????? ???????. ????????? ???????, ??????????? ??????, ???? ?????? ? ??????. ?????????, ??????????? ? ?????????? ???????? ????????????? ????????? ????????.
Thoughtful Click Picks – Well-laid-out content and intuitive navigation make exploring the site enjoyable.
??????? ??????? ?????????????? https://e-battery.ru ??????? ??? ???????? ??????????? – ???????? ??????? ??? ?????????? ?????? ????????? ???????. ?????? ??? ?? ??????????, ????????, ?????????, ?????? ?????? ? ??????? ?????????????????? ??? ??????????? ????????????
????? ?????????? ????????? ?????????? ???? ???????????????? ????????? ??????? ??? ?????????? ? ??????????? ????. ????????????? ?????????, ????????? ??????, ??????? ????, ????????????? ? ??????????. ??????? ??????????? ????????, ???????? ? ?????????? ?????????.
????????? ???????? ?????? ?????????? ?? ?????????? ?? ?????? ?????????, ? ?????? ?????? ????? ??? ??????? ??????? ?? ??????. ? ?? ?????: ????????? ???????? ? ???????? ???????????, ??????????, ???????????, ? ????? ?????????????? ????????? ?? ????? – ?? ??????? ????????? ?? ?????? ??????. ?? ????? ????????? ??? ?????????? ? ??????????, ?? ??????? ??? ? ?????? ?????. ???? ???? – ???????????? ??? ??????????? ???????, ????? ?? ????? ??????????? ?????? ????????? ? ????? ?????.
????? ???????????? bestakbspb.ru ?????? ??? ?? ????? ? ?????? ????, ??????? ????? ??????? ? ????????? ????. ????????, ?????????, ???????? ??????? ? ?????? ? ?????????.
The best is right here: https://vps38372.onzeblog.com/39034492/get-started-with-free-online-puzzle-games
get x casino ??????????? t.me/getx_site_official .
??????????? ???? ?????? fen-ds-1.ru .
Clickping Experience Hub – Well-structured layout with thoughtfully arranged content, very enjoyable to browse.
???? ??????? ?????? ??? ????? ? ????????? ??????????? ???? ?????? fen-d-1.ru .
?????? ?????? ??????? ??? ????? ??????????? ???? ???? ? ????????? http://www.fen-ds-3.ru .
dyson com ??????????? ???? http://stajler-d-1.ru/ .
?????????? ????????????? ?????? ????? ??? ???????
https://gunimmo.lu/agent/kendrickzhang/
???????? ?????? ???????? ???????? ?????? ???????? .
??????????? ??????? dyson https://stajler-d-2.ru/ .
???? ??????? ?????? ??? ????? ? ????????? ??????????? ???? ?????? http://stajler-d.ru .
Creative Essentials Hub – Well-designed layout, visually pleasing items, and a seamless shopping experience.
?????? ?????? ??????? ?????? https://fen-d-2.ru/ .
Clickping Central – Items and sections arranged thoughtfully, making exploration seamless.
????? ?????????? ????????? ??????? ????????? ? ??????? ???????????????? ????????? ??????? ??? ?????????? ? ??????????? ????. ????????????? ?????????, ????????? ??????, ??????? ????, ????????????? ? ??????????. ??????? ??????????? ????????, ???????? ? ?????????? ?????????.
???????????????? ????????? ???????? ?????????? ??? ?????? ? ???????? ???????. ????????? ???????, ??????????? ??????, ???? ?????? ? ??????. ?????????, ??????????? ? ?????????? ???????? ????????????? ????????? ????????.
??????? ??????? ?????????????? https://e-battery.ru ??????? ??? ???????? ??????????? – ???????? ??????? ??? ?????????? ?????? ????????? ???????. ?????? ??? ?? ??????????, ????????, ?????????, ?????? ?????? ? ??????? ?????????????????? ??? ??????????? ????????????
?????????? ?????????? ??????????? ?????? — ??? ?????
https://khmerhd.tv/@vitohenson3479?page=about
????? ???????????? ???????????? ????????????? ??? ?????? ??? ?? ????? ? ?????? ????, ??????? ????? ??????? ? ????????? ????. ????????, ?????????, ???????? ??????? ? ?????? ? ?????????.
????? ????????? ?????????? ??? ????????????? ???? ? ????????? ??????? ?? ???? ???????? ???? https://stroi-garantiya.ru/ – ?? ?????? ?? ??????????????? ??? ???????? ???????. ?? ????? ?? ??????? ????????? ?????????? ?????????. ??? ????????????? ???????????? ? ?????? ????????. ? ??? ??????? ? ????????????? ????.
Delicious – here: https://vps86048.blog2learn.com/86420901/build-your-own-puzzle-experience-online
????? ????????? ????? https://shams-arab.ru ???? ? ????????? ????????, ???????????? ? ?????????. ????????? ??????????, ???????, ??????? ? ??????????? ?????. ??????? ???????? ?? ????????, ????????? ? ?????? ??????? ???????.
?????? ?????? https://students-helper.ru ????????? ? ???????? ????????. ????????, ???????????, ????????, ?????? ? ???????????. ?????????????? ??????, ?????????? ??????, ????????? ?? ??????????? ????????????? ? ??????????????????.
Commerce Essentials Hub – Dependable site with simple navigation and an excellent product range.
????? ???? https://obucheniebpla.ru ???????? ?????????? ???????????? ???????????? ?????????? ? ???? ? ??? ???????????. ???????? ???????, ?????? ????????????, ?????????, ?????????????? ? ?????????? ?????????? ?????? ?? ??????????? ??????????.
???????? ????????? https://mother-massage.ru ??????? ? ?????????? ??? ????? ?? ???????? ?? ????. ???????????? ???????, ?????????? ???????, ???????? ???????? ? ?????????? ???????? ??????. ????????? ???????????, ????????? ???????????? ? ??????????? ?????????.
??????????????? ???? https://za-obrazovanie.ru ? ????????? ???????? ? ???????? ???????. ?????? ? ????????????, ??????????, ??????????, ????????? ? ?????? ? ?????? ? ?????????. ????????, ????? ? ???????? ?????????.
Clickping Curation Hub – Carefully curated items and structured design, making the site easy to explore.
?????????? ?????? — ??? ??????? ? ?????? ???????
https://mexicocoastal.com/author/maynard5219967/
modernwellbeingstore – Wellbeing-focused items are appealing, site navigation makes shopping very simple.
Soft Petal Home – Every item is delicate, and navigating the store feels smooth and natural.
Thoughtful Design Hub – Neat sections and intuitive navigation, browsing feels natural and enjoyable.
????? ????????? ????? https://shams-arab.ru ???? ? ????????? ????????, ???????????? ? ?????????. ????????? ??????????, ???????, ??????? ? ??????????? ?????. ??????? ???????? ?? ????????, ????????? ? ?????? ??????? ???????.
????? ???? https://obucheniebpla.ru ???????? ?????????? ???????????? ???????????? ?????????? ? ???? ? ??? ???????????. ???????? ???????, ?????? ????????????, ?????????, ?????????????? ? ?????????? ?????????? ?????? ?? ??????????? ??????????.
?????? ?????? https://students-helper.ru ????????? ? ???????? ????????. ????????, ???????????, ????????, ?????? ? ???????????. ?????????????? ??????, ?????????? ??????, ????????? ?? ??????????? ????????????? ? ??????????????????.
??????????????? ???? https://za-obrazovanie.ru ? ????????? ???????? ? ???????? ???????. ?????? ? ????????????, ??????????, ??????????, ????????? ? ?????? ? ?????? ? ?????????. ????????, ????? ? ???????? ?????????.
???????? ????????? https://mother-massage.ru ??????? ? ?????????? ??? ????? ?? ???????? ?? ????. ???????????? ???????, ?????????? ???????, ???????? ???????? ? ?????????? ???????? ??????. ????????? ???????????, ????????? ???????????? ? ??????????? ?????????.
?????????? ????????????? ?????? ??????? ????? ???? ????
https://okotcha.com/kendrafollansb
Site web de pari foot rdc: paris sportifs, championnats de football, resultats des matchs et cotes. Informations detaillees sur la plateforme, les conditions d’utilisation, les fonctionnalites et les evenements sportifs disponibles.
Site web 1xbet congo – paris sportifs en ligne sur le football et autres sports. Propose des paris en direct et a l’avance, des cotes, des resultats et des tournois. Description detaillee du service, des fonctionnalites du compte et de son utilisation au Congo.
La plateforme telecharger 1xbet apk: paris sportifs en ligne, matchs de football, evenements en direct et statistiques. Description du service, marches disponibles, cotes et principales fonctionnalites du site.
dyson ??? ???????? dyson ??? ???????? .
???? ???????? ???????? ?????? ???? ???????? ???????? ?????? .
Thoughtful Layout Hub – Neat design with carefully organized items and seamless browsing.
La plateforme en ligne telecharger 1xbet burkina faso: paris sportifs en ligne, matchs de football, evenements en direct et statistiques. Description du service, marches disponibles, cotes et principales fonctionnalites du site.
?????? ??????? ??? ????? ?????? ???? ??????????? ???? ? ????????? fen-ds-1.ru .
Application mobile 1xbet apk. Paris sportifs en ligne, football et tournois populaires, evenements en direct et statistiques. Presentation de l’application et de ses principales fonctionnalites.
Curated Petal Hub – Each item is gentle and attractive, and browsing the website is simple.
?????? ?????? ??????? ??????????? ???? https://www.stajler-d-2.ru .
??????????? ??????? ?????? http://fen-d-1.ru .
dyson official dyson official .
Modern Wellbeing Finds – Browsing is effortless, with products thoughtfully selected for health and comfort.
Everyday Goods Marketplace – Items are top-notch, purchasing is simple, and the site is user-friendly.
cheap electronics online EU ?????? iPhone ?????? ? ?????? ????? ????? ????????! ??? ????????-??????? ?????????? ??????? ????? ???????? ???????, ??????? iPhone 15 Pro Max ?? ????? ???????? ???? ? ??. ????? ????? ????????? ???????? ? ??? ???? ??????? iPhone ? ??????????????? iPhone ? ?????????. ?? ???????? ???? ??????????????? ??????? ????????????? ?? iPhone ? ??????!
?????????? ?????????? ??????????? ?????? — ??? ???????? ?? ???????
https://propi.id/author/amelie33a36610/
Future Crest Finds – Browsing is fast and intuitive, with forward-looking design selections.
?????? ??????? ??? ????? ???? ? ????????? ?????? ??????????? ???? https://www.stajler-d-1.ru .
Elegant Home Picks – Navigation is intuitive, highlighting daily essentials beautifully.
Wildshore Home & Lifestyle – Each product is appealing, and navigating the store is simple.
?????????? ????????????? ?????? — ?????? ???????
https://seychelleslove.com/@kellemcneill82
Consumer Essentials Picks – Fast shipping, careful packaging, and excellent assistance from support.
??? ?????? ?????? ???????? stajler-d.ru .
Premium Home & Lifestyle – Each item is appealing, and navigating the website feels effortless.
?????? ??????? ??? ????? ??????????? ???? ? ????????? ?????? ???? http://www.fen-d-2.ru/ .
Curated Everglen Picks – Navigation is effortless, highlighting charming nature-themed products.
Mindful Design Market – Eco-friendly and thoughtfully organized, checkout is simple and quick.
Clickping Selection Hub – Thoughtfully arranged sections with smooth flow and clear visuals.
modernpremiumhub – Modern and premium items feel well curated, browsing is effortless today.
?????????? ?????????? ?????? ?????? — ????????? ?????????
https://testedwebsite.us/realestatee/agent/laynemccurry71/
https://tanoshikoto.net/ ?????????????????????????????????????????????????????????????????????????????????????????
Marketplace Picks Hub – Exploring the site is fun, navigation is straightforward and clear.
Golden Craft Collection – Every product is skillfully made, and browsing the website is effortless.
?????? ???? ????? ??????? ??? ?????? – ??? ?? ?????? ????? ??? ????, ??? ????? ?????????, ??? ????????????? ?????, ?????????, ??????? ?, ??????? ??, ??????? ?? ??????? ???????. ??? ?????? ??????? ????? ??????????? ????????? – ??? ??? ???????? ??????. ???? ??????? ?????? ?????????? ?? ?????? ??????? ????? ??? ? ?????? ??????, ?? ? ??????????? ??????, ????????? ????????? ? ???????? ??????? ????.
everydaypremiumessentials – Everyday essentials are high-quality, shopping here is quick and pleasant overall.
??? ????? ???????? ???????? ??? ????? ???????? ???????? .
???????????? ??? dyson ???????????? ??? dyson .
Curated Fall Essentials – The interface is clean, showcasing visually appealing autumn products.
?????? ??????????? ??????? ?????? — ???????? ??????? ? ?????
https://vezonne.com/@lyndaesquivel6?page=about
?????? ??????????? ???? ??? ???? https://www.dn-fen-4.ru .
??????? ?????? ??????????? ???? http://www.fen-ds-1.ru .
Creative Living Hub – Navigation is seamless, highlighting home items that feel fresh and inspiring.
Global Essentials Store Hub – Excellent quality products, well-curated and easy to explore.
Global Creative Picks – Thoughtfully curated unique items, browsing feels lively and enjoyable.
Autumn Boutique Picks – Smooth browsing with each item reflecting cozy and charming autumn vibes.
clearer options – Reinforces the value of simplicity when weighing possibilities.
?????????? ?????? — ??? ?????? ? ????????
https://www.best-property.ae/author/christinmanna6/
Stylish Creative Marketplace – Intuitive layout with thoughtfully selected home items for easy shopping.
?????? ??????? ?????? ??????????? http://www.fen-d-1.ru .
Wildridge Floral Collection – Every item feels vibrant, and exploring the website is effortless.
?????? ??????? ??? ????? ?????? ???? ? ????????? ??????????? ???? http://www.stajler-d-2.ru .
La plateforme 1xbet apk: paris sportifs en ligne, matchs de football, evenements en direct et statistiques. Description du service, marches disponibles, cotes et principales fonctionnalites du site.
Site web 1xbet inscription rdc – paris sportifs en ligne sur le football et autres sports. Propose des paris en direct et a l’avance, des cotes, des resultats et des tournois. Description detaillee du service, des fonctionnalites du compte et de son utilisation au Congo.
Eco Essentials Hub – Mindfully arranged products, shopping is easy and visually satisfying.
Responsible Essentials Marketplace – Browsing is smooth, highlighting thoughtfully sourced products throughout.
Site web de pari foot rdc: paris sportifs, championnats de football, resultats des matchs et cotes. Informations detaillees sur la plateforme, les conditions d’utilisation, les fonctionnalites et les evenements sportifs disponibles.
?????????? ?????????? ???????????? ?????? — ????????? ????????
https://daterondetjolie.fr/@gerardscherer0
La plateforme en ligne 1xbet burkina apk: paris sportifs en ligne, matchs de football, evenements en direct et statistiques. Description du service, marches disponibles, cotes et principales fonctionnalites du site.
Moonridge Picks Marketplace – Navigation is simple, highlighting distinctive and fun products.
new opportunities – A comfortable space for discovering fresh ideas at your own pace.
dyson ??????????? ???? ? ?????? stajler-d-1.ru .
?????? ???? ??????? ?? ?????? ??????? ??????-?????? ? ???? ? ???????? ?? ??????????? ??????????, ?? ??????? ???????????? ??????? ? ?????????? ? ??????? ?????, ??? ???? ????? ?? ??????? ????????????? ??????? ?? ?????, ? ?? ?? ??????? ??????????.
globalpremiumcollective – Global premium items are unique, website is user-friendly and visually appealing.
???? ????? ???????? https://bestyleacademy.ru ????????????????? ????????. ??????? ?????????, ?????????? ?????????, ?????? ?? ????? ? ?????????? ???????. ????????, ??????????? ? ???????? ???????????? ??? ?????? ? ??????.
????? ???????? https://vdskill.ru ? ??????????????? ??? ??????? ? ????????????????. ???????? ?????, ????????????, ?????? ? ???????????. ???????????? ???????, ????????? ??????????? ? ?????????? ??????????? ??? ?????.
??????????????? ???? https://educationruss.ru ?? ???????? ?? ????????. ???????????? ? ????????, ???????? ?????, ??????? ???????????, ?????????, ????????? ? ????? ?????????. ???????? ?????? ? ???????????? ??? ???????????? ? ?????????.
Ethical Consumer Hub – Informative and clean design, items meet expectations and feel reliable.
???????????????? ????? ???????????? ???????????? ?????? ??????, ????????, ???????????? ? ??????????? ??????? ? ???????????? ??????????. ???????? ???????? ????????? ?????? ? ????????? ?????? ??? ??????.
Curated Urban Essentials – Smooth browsing highlights stylish and distinctive urban items.
Application mobile 1xbet burkina. Paris sportifs en ligne, football et tournois populaires, evenements en direct et statistiques. Presentation de l’application et de ses principales fonctionnalites.
??????????? ?? ????? — ?????????? ?????????? ??????????? ?????? ?????
https://demo.playtubescript.com/@hugomackennal2?page=about
??? ?????? ?????? ???????? ??? ?????? ?????? ???????? .
dyson ??????????? ??????? http://www.stajler-d.ru .
???????? ?????? ?????? ???????? ?????? ?????? .
??????????? ???? dyson http://fen-ds-3.ru/ .
?????? ??????? ??? ????? ???? ??????????? ???? ?????? ? ????????? http://www.fen-d-2.ru .
moderncollectorsmarket – Modern collectibles feel high-quality, shopping experience is seamless and effortless.
purposeful path – Emphasizes finding meaning behind personal goals and choices.
Global Essentials Collection – Impressive selection, smooth browsing experience, and high-quality items.
Ethical Lifestyle Market – Products are responsibly sourced, browsing and checkout are effortless.
Cheat Empire — ??? ????????? ?????? ? ???????? ??????????? ? ??????? ?????: Roblox (???????), Genshin Impact (?????? ??????), Standoff 2 (???????? 2), PUBG Mobile (???? ??????), Counter-Strike 2 (?? 2) ? ?????? ??????. ????? ?? ??????? ??????????? ????, ??????? ? ???? ??? ???????, ????? ?? ???????????, ??????? ?????????? ? ?????? ??? ????????. ??? ????????? ????????? ? ????????? ??? ??????????. ?????????? ??? ????????! https://cheat-empire.fun/
Conscious Lifestyle Market – Website is responsive, browsing feels natural, and product range is top-notch.
?????? ??????????? ??????? ?????? ???? ?????? ??????
https://git.881221.xyz/carmelodd30439
???????????????? ???????? ???????? ? ???????????? ??????, ????????, ???????????? ? ??????????? ??????? ? ???????????? ??????????. ???????? ???????? ????????? ?????? ? ????????? ?????? ??? ??????.
??????? ?????? ??? ????? ? ????????? ?????? ??????????? ???? ???? http://fen-ds-1.ru .
???? ????? ???????? https://bestyleacademy.ru ????????????????? ????????. ??????? ?????????, ?????????? ?????????, ?????? ?? ????? ? ?????????? ???????. ????????, ??????????? ? ???????? ???????????? ??? ?????? ? ??????.
??????????????? ???? https://educationruss.ru ?? ???????? ?? ????????. ???????????? ? ????????, ???????? ?????, ??????? ???????????, ?????????, ????????? ? ????? ?????????. ???????? ?????? ? ???????????? ??? ???????????? ? ?????????.
????? ???????? https://vdskill.ru ? ??????????????? ??? ??????? ? ????????????????. ???????? ?????, ????????????, ?????? ? ???????????. ???????????? ???????, ????????? ??????????? ? ?????????? ??????????? ??? ?????.
Curated Wildbrook Outdoors – Easy-to-use layout and distinctive products make shopping enjoyable.
shape your future – Reinforces the idea that progress starts with intentional choices.
????????? ?????????? «???????????» ? ?????? ?????????? ???? ????????? ? ????????? ????????????? ???????????? ????????, ??????? ????????? ?????? ? ??????? ?? ???????????. ?? ????? https://vozrogdenie1.ru/ ??????????? ???????? ??????? ????????? ??????????, ?????, ???????????? ????? ? ???????????, ? ????? ?????? ?? ????????, ????????? ? ???????????????. ??????????? ???????????? ? ??????? ??????? ????????? ???????? ?????????????? ?????? ? ?????? ?????????? ? ???????????? ???????????, ????? ????????? ???????? ???????? ? ?????????? ?????????? ? ????????????.
Green Design Hub – Responsible choices showcased cleanly with an intuitive browsing experience.
?????????? ?????????? ??????? ?????? — ????? ?????
https://git.lucas-michel.fr/alannalui37491/alanna2019/wiki/tamozhennoe-oformlenie-87P
Sunrise Studio Marketplace – Browsing feels natural, with carefully curated and inspiring products.
progress together – Highlights the value of advancing with a supportive community.
??? ?????? ??????????? ???? ???? http://fen-d-1.ru/ .
??????? ?????????? ?????????? ? ??????? ?????? — ?????? ? ??????
https://git.yinbonet.cn/reynabonilla69/reyna1985/wiki/tamozhennoe-oformlenie+36T.-
??? ?????? ??????????? ???? ???? https://dn-fen-4.ru/ .
??????? ?????? ?????? ??????????? ???? ??????? ?????? ?????? ??????????? ???? .
Sourced Lifestyle Store – Well-arranged items with genuine feel and easy navigation.
??? ?????? ?????? ??????????? ???? https://stajler-d-1.ru/ .
????? ??????? ?????????????? ??????? ??? ????????? ???????? ???????? https://www.akb24v.ru/ ? ?? ??????? ????????? ??????? ??????? ?? ???? ??? ?????? ??????? ??? ???. ???????? ????? ??????? ? ??? ? ??????? ? ?? ????? — ???????????? ??? ??????? ???????? ??????????????, ? ????? ??????? Still, Jungheinrich, Yale, Hangcha, Daewoo, Toyota ? ?????? ??????. ????????? ?? ?????.
????? ?????? ?????? 2026 ????????, ??? ???-10 ??????? ??? ??????? ?????????? ????? ? ????? ???? ????????? ??????-??????! ??????? ????!
??????? ???????? ??? ???????, ?????????? ?????????? ??????? ??????
https://gitea.yanghaoran.space/jacksonried526
full potential tips – Offers actionable advice for unlocking hidden abilities in everyday life.
Cactus Casino (???????) ?????? ?????? ?????? ? ?????
? ???? ???? ?????? ?????? ?????? ?????????? ????????? ?? ????? ????????? ??????? ? ??????????? ????????? ??? ???, ??? ???????? ???????????? ??????? ??????. ?????? ???????????? ?? ???????, ??????? ????? ??????? ????? ??????, ??????? ??????? ? ??????? ???????. ????????? ?????????? ?????? ??????????? ???? Cactus Casino ???????? ??? ????????, ??? ? ??????? ?????????????, ??????? ????? ?????? ? ????? ?????? ? ????????? ? ??? ?????? ??????.
?????? ?????? ???????? ?????? Cactus
??????? ??????????? ???????? — ?? ???????????????. ?????? Cactus ?????????? ???? ?? ?????????? ??????? ???????????, ??? ???????????? ???????????? ??????? ? ??????. ???????????? ????? ????????? ???????????? ????????, ??????????, ???????, ?????????? ???? ? live-??????.
? ?????? ????????????? ?????????:
• ?????????? ?????? ? ????????? ? ?? ? ??????????;
• ??????????? ????????? ??? ??????????;
• ?????????? ????? ? ?????? ??????, ??????? ???????? ??? ??????? ????? ????;
• ????????? ????????????? ?????????????.
? ????????? ??? ??????? ?????????? ?????, ??? ????? ???????? ?????? ? ??????????? ????????? ??? ?????? ? ????????.
?????????????? ????? ? ??????? ??????? ?????? ??????
?? ?????? ??????? ???? ?????????????? ???????????, ??????????? ????????? ??????? ? ???????? ???????? ? ?????????? ??????. ?????? ?????? ??????????? ?????????? ?????, ??????? ???????????? ????? ???????? ????? ??? ???? ???????????? — ?? ??????? ?? ??????? ? ??????????? ??????????.
????????? ?????????? ????? ?????????? ?? ???????? ???????: ??? ?????? ??????, ??? ???? ??????? ? ????????? ????????????.
???? ? ?????? – ?????, ???? ? ?????????? ????????
????? ???????? ???????? ????? ?? ????????? — ????? ???????? ???????? ?????? ??????: ?? ?????-??????? ?? ??????????? ??? ? ?????-???????? ? ?????????????? ??????????.
????? ????, ?????? ?????? ?????? https://kaktuskazino.site ?????????? live-??????, ??? ????? ????????????? ????????? ????????? ???? ????????? ???? ? ?????? ????????. ?????????? ???? ????? ???????, ????????? ? ??????? ???????? ???, ??? ???????????? ????????? ???? ? ??????????? ?????????.
??? ?????? ?????? ? ??? ????? ????? ???????
????? ?????? ????, ?????????? ?????? ??????? ??????????? ? ????????? ?????? ??????? ????????. ????? ????? ????? ???????? ????? ????????????? ???? ? ????????? ?????. ?? ??????? ?????????? ??????? ????????? ???????????? ?????? ? ?????? ??????, ????????? ???? ???????????? ?? ?????????? ??????? ??????? ? ?????????? ???????.
???????? ????? ???????? ? ??????????, ??????? ???????? ?????? ? ?????? ????? ?????????? ? ??????? ?? ???????? ??????.
??????????? ???? Cactus Casino: ???????????? ? ????????????
??????????? ???? Cactus Casino ???????? ????????????? ? ????????????? ?????????? ??????????, ??? ????????? ????????????? ????????? ?????????? ??? ????????. ????????? ?????????? ????????????????? ?????????? ????????? ?????, ????????? ???? ??? ?????????? ??? ???????? ???????? ? ?????????????.
?????????? ?????????? ? ??????????? ????????? ?????? ???????? ??????? ??? ???????, ??????? ???????????? ???????????? ???? ??? ????????.
????? ?? ????????? Cactus Casino
???? ???????????? ????? ?????????? ????????, ??????? ????? ????????? ? ??????? ?????????, ?????? ?????? ?????? ????? ????? ?????????? ?????????. ????????? ???????, ?????????? ?????? ????? ? ??????? ???????????? ??? ?????? ????????? ?????????? ???????? ??? ????????, ??? ? ?????????? ???????.
?????? ?????? ??????? ??? ????? ??????????? ???? ???? ? ????????? http://fen-d-2.ru .
?????? ??????? ??? ????? ?????? ??????????? ???? ???? ? ????????? stajler-d.ru .
Mindful Marketplace Hub – Organized products with seamless browsing and intuitive interface.
?????????? ?????????? ?????? ?????? — ?????
https://investorshometown.com/author/ktxwendi109831/
dyson ??????????? ??????? http://www.fen-dn-kupit.ru/ .
idea collaboration hub – Points toward a central place for ideas to connect and grow.
???????????????? ???????? prp ???????. ????????? ??????????? ???????, ????????? ???????????? ? ?????? ?????? ? ??????????. ??????, ???????? ? ????????? ?? ???? ?????? ????????.
?????????? ??????????? ?? ????, ?????????? ?????????? ??????????? ??????
https://lnky.pk/ArJgl
Curated Treasures Hub – Carefully selected items with smooth navigation and clear layout.
kickstart progress – Highlights taking proactive steps toward personal growth.
?????????? ????????????? ?????? ?? ???? ???? ?????
https://myspectator.com/author/lonnieali6710/
???????????????? ????????????? ????. ????????? ??????????? ???????, ????????? ???????????? ? ?????? ?????? ? ??????????. ??????, ???????? ? ????????? ?? ???? ?????? ????????.
???????????????-??????????? ???????? «????????-?????» ?? ????????????? ???????????????? ?? ??????????? ?????????? ???????? ??? ??????? ? ???????? ????? ?????????. ?? ????? http://express-svyaz.ru/ ???????????? ?????? ?? ??????? ? ???????????? ?????? ???????????????, ?????????, ???????-???????? ????????????, ???? ? ????????????, ? ????? ?????????????? ? ???????????? ??????????????????, ????????? ?????? ? ???????? ??????. ???????? ???????? «??? ????», ??????? ?????????? ?????????? ? ??????????? ????????????, ??? ????????? ?????????? ???????? ???????? ?????????????? ? ??????? ??????? ? ?????????? ????????.
https://slokkasucouple.com/ ?????????????????????????????????????????????????????????????????????????????????????????????????????
Refined Everyday Hub – Orders delivered quickly, nicely packed and ready to use.
Explore Smart Concepts – A straightforward approach to discovering innovation online.
idea exploration – Focuses on browsing ideas that encourage thoughtful curiosity.
Navigate Smarter Options – A clean concept designed to help users discover optimal solutions.
?????????? ?????????? ?????? — ?????? ????????????? ??????
https://pokesoul.com/@kinasaucedo78
???????? Caspian Training Group ????? 24 ??? ??????? ????????? ??????? ?????????????? ???????? ? ??????????. ????? ???????????? ???????????? ????? ???????? ??????????? ??????, ????????????? ????????, ?????????????? ???????????? ? ??????? ????????? ??? ???????????? ???? ????????????. ?? ????? https://xn—-7sbecpcasfm0beeaecirc5b3a2g.kz/ ???????????? ????????? ?????????? ? ?????? ???????????, ?????????? ? ???????? ?????? ??? ????????????. ???????? ???????? ????????????????? ??????????? ??? «??????-??????» ? ???????????? ?????????? ? ????? ???????? ?????????? 100%.
motivationhub – Offers tips and ideas to start each day with focus and energy.
betteranswershub – Guides you to find practical and improved solutions every day.
Neironica https://neironica.ru ???????????????? ? ???????????????? ??? ???????? ???????-??????, ? ????????????? ?????????? ??????, ?????? ? ????? ?? ??? ???????
ideaexplosion – Helps unlock unlimited creativity and new ways of thinking.
purposeful creation – Reflects the idea of building with intention and lasting relevance.
Daily Essentials Hub Picks – Quick arrival, neatly packed, and very pleased with the quality.
??????? ?? ???????????????? ?????????? ????????????? ??????
https://repo.backender.de/krystynabeards
Innovative Thinking Hub – A simple platform designed to surface creative concepts without complexity.
Find Better Alternatives – A straightforward space to uncover improved solutions quickly.
Conscious Style Market – Thoughtfully selected products, navigating the site is simple and enjoyable.
??????? ??? ????? ?????? ???? ? ????????? ??????????? ???? ?????? http://www.fen-dn-kupit.ru/ .
solutionengine – Helps generate faster and smarter ways to address issues.
?????????? ?????????? ?????? ?????? — ??? ????????? ? ??????
https://speeddating.co.il/@aldaoflynn105
Neironica https://neironica.ru ???????????????? ? ???????????????? ??? ???????? ???????-??????, ? ????????????? ?????????? ??????, ?????? ? ????? ?? ??? ???????
thinkcreativelynow – Helps spark imagination and explore new innovative thoughts.
dailyfreshstart – Helps create a routine that promotes motivation and renewal.
?????? ???????? ??????????? ?????? ?????? ???????? ??????????? ?????? .
????????? ???????????? ????????????? ????????? ???????????? ????????????? .
Learning to Execution Path – Structured ideas that simplify taking action.
Positive Energy Daily – A simple site offering consistent inspiration and optimism.
????? ????????????? ? ??????????? ?????? ????????? ???????????????? ???????? ???? ?????? https://www.vesper.ru/ – ?? ???????????? ??????? ????????? ???????????????? ? 1992 ????. ? ??? ??????? ??????? ? ???????? ?? ??????. ???????????? ? ????? ?????????? ? ????????, ???????????? ???? ?? ????? ?????????.
Freedom of Thought – Inspires innovative thinking in a way that’s fun and actionable.
?????????? ??????? ?????? — ????? ? ?? ??????
https://ubuntushows.com/@coline24796098?page=about
Expand at the link: https://www.google.com/maps/d/u/3/edit?mid=1daxes-2lyhl5umzt9qvo4pu-wpkhsac&usp=sharing
??????????? ???????????? ? ???????? ??????? ???????, ??????????????, ???????????, ???????????????? ??????? ? ???????? ??????. ????????????????? ???????????, ?????? ??????????? ? ?????? ? ?????????.
speedyprogress – Guides you to regain drive and make progress quickly.
???????? ?? ???? ??? ????????? ??? ??????? ??????????????? ? ?????? ????. ????????? 3G 4G ???????? ??????? ????????. ????????? ????????? ????????? ? ???????????????. ?????? ????????? ? ??????????. ?????? ????? ?????????????? ??? ???????????? – https://podklychi.ru/
Apply and Execute – Simple guidance that supports consistent action after learning.
Innovative Freedom – Provides practical ways to explore ideas while maintaining creative freedom.
?????????? ????????????? ?????? — ?????? ????????
https://we2gotgame.com/videos/@melodeesherer2?page=about
Impact Through Action – A clean idea showing how thoughtful steps lead to real change.
learnprogressdaily – Helps maintain consistent learning and practical application of knowledge.
View on the website: https://gravatar.com/affable8849dee127
momentumengine – Keeps your progress steady and your goals within reach.
Daily Motivation Online – A simple approach for quick, encouraging content daily.
Growth Driven Network – A platform focused on linking development with practical outcomes.
?????????? ?????????? ??????????? ?????? — ??? ???????? ?? ???????
https://www.minnieleerealtyllc.com/agent/valeriaschafer/
imaginelab – Helps brainstorm ideas freely and inspire daily creativity.
Daily Project Launcher – Motivates taking action every day and moving projects forward.
???????? «??????» ? ??????? ???????????????? ?? ??????????? ??????????? ??????????? ???????????? ???????? ? ??????????????? ??????? ????? ????? ?? ?????????????? ?? ????????????. ????? ?????-??-? ???? (?? 10110-1), ?????? ?????????????? ?????????????? ?? ????? denors.ru ???????????? ??????? ?? ????????? ???????? ? ???????? ????????????, ?????? ???????????????, ????????? ? ???????? ??????? ??? ???????, ??????????????? ?????????? ? ??????? ????????. ??????????? ???????? ? ????????????????? ?????????????, ???????????? ???????????????? ?????? ? ????????? ?? 3 ??? ? ??????????? ????????? 24/7.
Options Made Simple – A clean framework that helps users explore ideas comfortably.
Daily Success Thinking – Motivational guidance that promotes consistent effort and mental clarity.
mydailystory – Encourages creating your personal story and moving forward confidently.
?????????? ????????? ??????? ?????? ?????? ? ?? ??????
https://code.dsconce.space/ralphpalombo92
strengthspotlight – Shines a light on abilities that support growth.
Path to Self-Improvement – A simple platform offering guidance and practical growth steps.
1xbet Android telecharger 1xbet pour android
1xbet Android gratuit telechargement 1xbet
Compte personnel 1xbet telecharger 1xbet pour android
Growth That Lasts – Thoughtful content focused on building long-lasting success.
focusdreams – Helps align actions with your vision for maximum impact.
??? ?????? ?????? http://www.fen-dn-kupit.ru .
nextlevelgrowth – Empowers progress to reach higher personal goals.
Step Ahead Slowly – A calm reminder that gradual movement still leads to improvement.
?????????? ??????????? ?? ????, ?????????? ?????????? ??????????? ??????
https://footage4k.ru/@frankiemccoll?page=about
More Value Insights – Helpful guidance focused on uncovering value through simple actions.
Handcrafted Lifestyle Hub – Each product is crafted carefully, browsing the site feels smooth and easy.
Effective Progress Hub – Practical ideas to move forward and tackle challenges efficiently.
Map Your Future – A simple platform helping users set priorities and see the bigger picture.
moveadvisor – Guides deciding on your next actions with focus and strategy.
habitsuccess – Guides forming routines that lead to tangible success.
??????? ?????? ?????? — ??????, ???? ?????????
https://git.healthathome.com.np/joeybarreto569
Value Building Resource – Clear explanations that remove unnecessary complexity.
Think And Create – A simple idea encouraging ongoing creativity and unique perspectives each day.
Learn Gradually – Structured guidance for efficiently acquiring new knowledge.
??????????? ???????????? ? ???????? ??????? ???????, ??????????????, ???????????, ???????????????? ??????? ? ???????? ??????. ????????????????? ???????????, ?????? ??????????? ? ?????? ? ?????????.
Hands-On Learning – A simple and useful site encouraging learning by taking action.
???????? ??????????? — ?????????? ?????????? ? ??????????? ?????? ??? ????????
https://git.temporaryname.org/madeleineecker
skillstoday – Pick up new skills that improve your productivity and life.
Thoughtful Outcomes – Carefully framed ideas aimed at meaningful and durable impact.
claritypath – Offers structured ways to reach mental clarity and plan effectively.
dailylearnhub – Encourages learning and putting knowledge into practice every day.
Creative Insights Online – A thoughtful space focused on inspiring imagination and innovative solutions.
Discover Your Potential – Focused ideas for uncovering growth opportunities and achieving goals.
?????????? ?????????? ? ??????????? ?????? ?????? ?? ???
https://gitea.noname-studios.es/juliostedman7
?????????? ??????????? ?? ???, ?????? ??? ??????? ? ????? ???????? ????? ? ????????? ??????????? ?????, ??????? ? ??????????????????????? West-atlas.com ?????????? ?????????? ?????? ? ????????? ???????? ?????? ???? ?????? ???????, ????????? ?????? ? ???????? ????????? ??????????? ??????. ??????? ?????????, ???????? ?????????? ????? ????????? ? ?????? ??????? ? ??????? ?????? ???????????? ???????? ??????? ? ??????. ???????? https://west-atlas.com/ ? ???????????? ?????? ????? ????? ????????!
??????? ?????? ??????? dzen.ru/a/aTBxq5NJAQ5rNagc .
???????????? ?????? ? ????????? dzen.ru/a/aTakePgcFg8RJbIM .
?????? ??????????? ???? ??? fen-dn-kupit-1.ru .
Learning That Matters – Clear, structured ideas that make knowledge acquisition impactful.
sykaaa casino ???? ??????????? ??? ?????????????????? ? ?? ????????? ?? ??????: ?????? ??? ?? Sykaaa Casino. ??????-?????? ?????????? ?????? ????????? ? ?????????? ??????? ?????????, ?? ?????? ??? ?????? «??????», ????? ????????, ? ??? ?? ?????? ????. ? ???? ?????? ? ???????? ???????? ? ???????????, ????????????, ????????? ? ???????, ??????? ????? ????????? ??? ???????? ???????? ?? ????? ??????, ??????? ???????????? ?????? ? ?????? ????.
Find What Works Fast – A motivating site to explore effective methods efficiently.
???????? https://accs-shop.com/ – ??? ??????? ????????? ?1 ? ??????????? ?????? ??????, ? ??????? ?? ??????? ?????? ???????? ? ??????? ????????????. ?????????? ????????? – ??? ?? ??????????? ??????? ??? ???? ??????????? ?????. ?????? ??????? ???????? ?????????? ???????? ????? ????????, ?? ?????? ???? ??????? ? ????????, ? ????????? ???????? ??????!
skillenhancer – Encourages building skills in areas that drive meaningful growth.
Build Value Daily – Practical steps to integrate value creation into everyday actions.
?????????? ?????????? ??????????? ?????? — ??? ?????
https://homerootsproperties.ng/author/rodrigo28w235/
clarityengine – Supports focusing on essential tasks to achieve desired outcomes.
??????????? ???? ?????? https://www.fen-dn-kupit.ru .
Start Growing Smarter – A straightforward vision centered on improvement, connection, and digital achievement.
visionexpander – Encourages seeing the bigger picture and acting boldly.
Imagination in Action – Motivating content that helps turn creative ideas into growth.
?????? ??????? ?????? ?????? ????????? – ??? ???????????? ? ???? ?????????? ?????? ???. ?? ??????? ??? ??? ?????????? ?????????? ?? ???? ?????? ??? ?? ?????? ????. ?? ????? ?? ??????? ????? ????? ????????? ??????? ?? ?????, ?????? ?????? ? ????? ??????? ???, ????????????? ??????? ? ?????????? ?? ????????? ??????? ????????? ? ??????????, ? ????? ???????? ????? ?? ????? ??????? ?????? ????.
?????????? ?????????? ??????????? ?????? ?????? ? ??? ????????
https://lawrencewilbert.com/read-blog/21664_tamozhennoe-oformlenie-40f.html
Unlock Growth Potential – A motivating platform helping users enhance mindset and daily performance.
Design Forward Picks – Well-curated stylish products, navigating the site is simple.
Immediate Progress Hub – Practical tips for taking actionable steps and moving forward today.
????????? ???????: ??????? ?????????? ? ??????: ?????? ? ????????? ??? ????? ?????
????? ? ????? ???????????? ??-??????, ????? ?????? ???????? ?????????? ????? ?? ????????? ?????????????? ???????? ? ???????? ??????. ?? ????? ???????????? ???????? https://ekskursii.open-anapa.ru/ ????? ???????? ???????????? ????????? ?? ????? ? ????? ?????????????? ???? — ?? ?????? ????? ?????-????? ?? «???????? ??????» ?????. ?????????? ??????????, ?????????????? ????????????? ? ??????????? ????????? ?????? ??????? ??????????, ?????????? ? ??-?????????? ?????????????? ??? ???? ?????.
creativedirections – Motivates discovering new ways and innovative approaches.
Pretty! This was an extremely wonderful post. Many thanks for supplying this information.
888phl.pro
???????? ? ???????? ??????? ?????? ?????? https://behruzoglu.com/ru/ – ??????? ????????????? ???????? ? ?????, ??????? ?????? ???. ???? ??? ????? ????????????????? ??????? ???? ???????? ? ???, ?? ????? ?????? ???????????. ??? ??????????????? ???????? ? ????????, ?????? ???????? ??????? ?????????, ??? ???????? ????????. ?????? ?????? – ????????? ??????? ???? ???????? ? ?????. ?????, ??? ????????? ????????????? ???????? ? ??? ??? ??????????????? ???????? ? ?????? ??? ???????? ??????? ???? ???????? ? ???????? ???? ???.
Focus And Direction – A practical place for refining goals and understanding purpose faster.
Different Ways Forward – Thought-provoking insights that encourage looking beyond the obvious.
<futurepossibilitieshub – Helps envision and explore possibilities for growth and success.
?????????? ?????????? ?????? ?????? — ??????? ??????, ??? ??
https://movieru.jp/portfolio/@donquaife94990?page=about
????? ???????? ????? «???????» https://kopirych.by ????????????? ??????????? ?????? ????????? ?????? ?? ??????, ? ????? ?????. ????????????? ?? ???????????????? ?? ???????????? ????????? ??? ??????? ? ???????. ????????????? ???????????? ???????????? ???????????? ? ?????????? ?????????? ???????????? ?? ?????? ??????? ?? ? ???????????? ?????.
Journey Launchpad – Supports taking the first meaningful steps with confidence.
Progress Hub Today – A focused platform for building forward motion and positive change.
thinkfreshdaily – Encourages new perspectives and inventive solutions every day.
inspireboost – Supports regaining focus and excitement for achieving goals.
Clarity Toolkit – Easy-to-use ideas that support clearer thinking right away.
??????? ?????? ?????? — ?????? ???? ? ?????
https://pattayavids.com/@arielr65341934?page=about
Clarity And Purpose – A simple approach helping people move toward purpose with ease.
???? ?????? ??????????? ???? ?????? – ??? ??????????? ????????? ??? ????????? ???????? ???, ???????????? ??????? ?????? ??????????? ? ???????????? ??? ????????. ?????? ????????? ??????? ?????????? ? ????????????? ?????????, ????????? ??? ??????? ???????, ??? ? ????????.
? ???? ??????? ???????? ??????? ?? ?????? ?????????? ????, ?? ? ???????? ?????????, ? ????? ??????? ???????? ????????????? ?????. https://fortuna-distillery.com/ ????????? ??????? ?????????? ??????? ??????? ? ??????????? ?????????? ??? ???????? ?????????? ??????. ?? ????? ??????????? ??????? ?? ??????? ??????? ??????????? ??????????? ????????.
Global Ideas Network – Seamlessly connect with thinkers and innovators around the world.
?????? ???????????? ?????? ??? ???????? ????????????????? ???????, ????????, ??????? ? ??????? – ??? ?????? ?? ???????? ? ?????????????.
??????? SEO ?????????? ???????? ?????? ? 2007 ???? ??????????????? ?????????? ???????????? ?????? ? ????????? ???????? Google ? Bing. ????? ??? ??????????? ???????? ?? ????????? private-seo.com/ru/ ??????????? ?????? ?????? ????? ?? ???????????: ??????????? ?????, ?????????? ?????????????? ????????? ???????????, ????????? SEO ? ?????? ? ?????? ???????????? GEO. ?????????? ????? ????? ?????? ?????? ??? ???????????, ??????????? ?????? ??????? ? ???????? ? ??????? ??????? ?? ????????? ??????-????????????, ??? ???????????? 80% ??????????, ?????????????? ????? 5-10 ???.
?????? ? ????????????? https://prostostroy.com ??? ??? ? ???? ??????? ? ???????. ?????????? ??????, ?????????? ??????, ?????? ?????????? ? ??????????. ?? ?????????? ?? ????? – ???, ??? ????? ????? ??? ????????? ???????.
??????? ??????? ????? https://inpenza.ru ?????????? ? ??????????. ?? ???????? ??? ???????? ???????, ???????????? ? ????? ? ?????????? ???????. ?????? ??????????, ?????, ???????? ?????????? ??? ??????? ??????. ??? ???????? ???????? ????????.
forwardmindset – Helps cultivate forward-thinking habits and plan ahead effectively.
????????? ??????? ????? ?????? ?????? ???? – ??? ?????? ??? ? ???????? ??????? ? ??????????????? ????? ? ????? ????. ????????? ????????????? ?????? ???????? ???????? ?????? ??? ????????????? ? ????????? ???????? ?????? ???? ?? ?????? ????.
???? ??????? ?????? ??? ????? ? ????????? ??????????? ???? ?????? fen-dn-kupit-1.ru .
??????
?????? ?? ?????? — ?????????? ?????????? ?????? ?????? ?????? ??????
https://quenly.com/@rogersimonetti
Shareable Concepts Hub – A modern concept encouraging users to find ideas others will appreciate.
https://g4sky.ru/ – ????????-??????? ??? ??????????? ???, ?????, ????, ???????? ? ??????. ????? ?? ??????? ?????????? ????, ????????, ??????? ? ????????. ???????????????!
pathforwardhub – Helps you plan your next steps and move forward confidently.
positive progress habits – It encourages forward motion through healthy routines.
strengthsexplorer – Helps individuals uncover strengths and plan personal growth.
???? ?????? ???????? ???? ?????? ??????: ????????? ???? ????? ?? ?????? ? ??????? ???????? ? ???????. ?????????????? ??????, ?????????? ??????, ???????? ? ?????? ?????? ???? ??? ? ???? ??????.
start smart journey – This platform helps users begin a smart journey and reach objectives efficiently.
opportunitylaunchpad – Helps turn new possibilities into real achievements quickly.
??????? ?????? ?????? — ?????? ???? ? ?????
https://skpropertiesuae.com/author/luellaw082966/
??????? ??????? ????? https://inpenza.ru ?????????? ? ??????????. ?? ???????? ??? ???????? ???????, ???????????? ? ????? ? ?????????? ???????. ?????? ??????????, ?????, ???????? ?????????? ??? ??????? ??????. ??? ???????? ???????? ????????.
???? ?????? ??????? ???????? ?????????? ???? ?????? ?? ???? ??????????, ????? ???????? ??????? ? ??????? ?????? ?? ???? ????? ? ????????. ??????? ? ????? ????? ? ? ????? ?????.
?????? ? ????????????? https://prostostroy.com ??? ??? ? ???? ??????? ? ???????. ?????????? ??????, ?????????? ??????, ?????? ?????????? ? ??????????. ?? ?????????? ?? ????? – ???, ??? ????? ????? ??? ????????? ???????.
?????? ?????????? ??????????? http://www.arenda-ekskavatora-pogruzchika-6.ru .
????????????? ???? ?? ???? http://www.gidroizolyacziya-czena.ru/ .
?????? ru ?????? ru .
???? ?????? ??????????? ? ?????? ???? ?????? ??????????? ? ?????? .
??? ? ???????? https://zapisnapriemrostov.ru ? ???????? ? ????? ?????! ???????? ?????? ? ??????????? ???????, ????????????? ???????????? ? ???????? ????????? ??? ??????????? ????????? ????????????. ?????? ? ????? ? ?????? ?????? ??????!
edgeplanner – Helps identify and maximize strengths in a strategic way.
????????????? ? ?????? https://ctoday.ru ???, ??? ????? ?????. ?????????? ??????? ??? ??????????? ??? ???? – ??? ???????? ????????. ?????????? ?????????? ? ??????????, ???????????, ??????? ? ??????????? ????????. ? ???? ?????? ?????? ????? ? ????????!
Empowerment Tips Fast – A practical approach to feeling strong, confident, and ready to act.
??????? ??????? ?????? ??????? ???????? ??????? ???????????? ?????. ?????? ?????? ?? ???????? ?????? ? ??????? — ??????????? ???????. ????? http://topovye-kazino-onlajn.biz.ua/ ????? ??????????? ? ?????????????. ??????? ?????? ?????? ?? ???????? ? ??????? ??????? ???????.
?????? ?????? ? ??????? ????? ??? ???????? — ????????, ?? ??? ????.
????? ?????????? ?????? ?????? ?????? ?? ?????. ?????? ?????? ??????? ?????? ????????? ???????? ??????. ????? ?????? ?????? ?????? — ??????? ?????????????. ?????? ?????? ????? ???? ????? ????????????? ? ?????????.
optimistic growth path – The approach encourages confidence in everyday actions.
strengthgrowth – Supports growth by focusing on existing strengths.
payday loan
Ethical Design Picks – Well-curated items, site layout makes browsing enjoyable and smooth.
????
????? ??? ??????? ?????????? ?????? ?????? — ??? ??????? ?? ????, ???????
https://tinyurl.ee/changdowden945
smart journey strategies – The platform highlights actionable tips to plan and execute a successful journey.
???????? ??????? ????????? ?????? ?????? ???? ????????? ??????????? ????? – ????????? ???, ????????? ?????????? ??????????. ?????? ????? ????? ??????????? ??????????? ???????????? ???????? ???????, ??? ???????? ?????????? ????? ? ???????? ?????? ? ???????? ?????????????. ??????? ??????? ????? ??????????? ??????????????? ? ???????? ??? ??????????? ???????, ???????????? ?????????? ? ?????????? ?? ??????.
?????? ?????? ?????? ?????? ????? ?????????? ??????? ? ????????. ?????? ?????? ??????? ???????? ??????, ??? ??????? ??????. ? ??????? ??????? ?????? ?????? ?????? ????? ????????????. ?????? ?????? ?? ??? — ??????? ??????? ??? ???????.
???????? ?????? ?????? ?????????? ??????????? ?????????.
??????? ???????? ?????? ?????? ???????? ????? ??? ??????. ?????? ?????? ??? ???????? ????? ???????? ????????. ?????? ?????? ?????? — ??? ???????????? ? ?????????. ??????? ?????? ?????? ??????? ???? ??????? ???????.
???????? ?? ???????? ????? https://www.chitai-gorod.ru/catalog/toys/lego-115391 ? ?? ??????? ?????? ???????????? LEGO ? ??????? ????????????, ? ????? ?????? ??? ??????? ??????????? LEGO ??? ???????. ?????????? ?????????? ????? ????????????? LEGO ? ?? ??????????? ??????? ?? ??? ??? ??????????!
??? ? ???????? https://zapisnapriemrostov.ru ? ???????? ? ????? ?????! ???????? ?????? ? ??????????? ???????, ????????????? ???????????? ? ???????? ????????? ??? ??????????? ????????? ????????????. ?????? ? ????? ? ?????? ?????? ??????!
discover better methods – The ideas presented make finding solutions easier and more efficient.
?????????? ?????????? ? ??????????? ?????? ?????? ?? ???
https://videos.recentstatus.com/@alenahilder471?page=about
????????????? ? ?????? https://ctoday.ru ???, ??? ????? ?????. ?????????? ??????? ??? ??????????? ??? ???? – ??? ???????? ????????. ?????????? ?????????? ? ??????????, ???????????, ??????? ? ??????????? ????????. ? ???? ?????? ?????? ????? ? ????????!
effectivegrowthplan – Supports creating actionable plans to reach growth targets.
?????? ??????? https://kfaktiv.ru ??????? ??????? ??????! ??????? ? ????????? ????????, ??????? ????????? ????? ??????. ?? ????????? ????????? ?? ?????????? ??????? ? ?????? ?????????? – ?????? ? ????? ?????, ??? ?????????? ? ????? ??????? ??????. ???? ?????? ?????????? ??????????!
??? ? ???????? ?? https://software-expert.ru ??? ???. ???????? ??? ???? ??? ??????? ????????????, ??????????? ????????? ? ??????????? ????????? ? ?????????? ???????????? ???????????. ???????, ??? ????????? ? ???????????? ?? ?? ????? ??????.
??? ? ??????????? https://providers.by ????????! ?????????? ???????, ??????? ?????? ????????????? ? ????????? ?????? ???????. ??????? ??????? ??????? ????????-??????????, ??????????? ????? ? ?????????. ?????? ? ????? ???? ?????????!
directioncoach – Supports finding clarity and staying aligned with your priorities.
warez
forwardideashub – Inspires thinking creatively and exploring new solutions consistently.
??????? ???? https://omaske.ru ? ????????? ?????? – ?????! ???????? ??????? ??????? ??? ???????. ???? ???????? ????? ??? ???? ? ????? ??????? ??? ??????????? ????, ???????? ??????? ? ??????? ?????????. ???????? ? ?????, ???????????? ???? ???? ? ???????!
confidence enhancement tips – The platform emphasizes stepwise strategies to strengthen self-belief.
fast cash
?????????? ?????????? ? ?????????? ?????? — ?????????? ? ????????
https://www.fastmarry.com/@terryjoe47432
guided progress ideas – It emphasizes practical ways to keep moving forward.
???????? ??????????? ??????? ??? ????????? ? ???????? ??????? ??????????. ?????? ??????, ?????? ???????, ????? ??????????. ????? ??????????? ?????? ? ??? ?????? ?????????. ???????????? ?????? ??????????? ?????. ?????????? ???? ??????????????: ?????? ??????????? ?????????? ? ?????? ??????
https://t.me/uhrenGermany026
?????? ??????? https://kfaktiv.ru ??????? ??????? ??????! ??????? ? ????????? ????????, ??????? ????????? ????? ??????. ?? ????????? ????????? ?? ?????????? ??????? ? ?????? ?????????? – ?????? ? ????? ?????, ??? ?????????? ? ????? ??????? ??????. ???? ?????? ?????????? ??????????!
???????????? ??????? ?????? ???????????? ??????? ?????? .
clarity mindset tips – The content encourages developing a mindset that fosters focused growth.
?????? ??????????? ???? ??????? ?????? ??????????? ???? ??????? .
?????? ??????????? ???? ??? ?????? http://www.fen-dn-kupit-1.ru .
??????? ???? https://omaske.ru ? ????????? ?????? – ?????! ???????? ??????? ??????? ??? ???????. ???? ???????? ????? ??? ???? ? ????? ??????? ??? ??????????? ????, ???????? ??????? ? ??????? ?????????. ???????? ? ?????, ???????????? ???? ???? ? ???????!
?????????? ?????????? ? ??????? ?????? — ??? ?? ??????
https://www.viettube.info/@natepoy2667071?page=about
structured growth ideas – The process makes growth easier to manage and track.
??? ? ???????? ?? https://software-expert.ru ??? ???. ???????? ??? ???? ??? ??????? ????????????, ??????????? ????????? ? ??????????? ????????? ? ?????????? ???????????? ???????????. ???????, ??? ????????? ? ???????????? ?? ?? ????? ??????.
??? ? ??????????? https://providers.by ????????! ?????????? ???????, ??????? ?????? ????????????? ? ????????? ?????? ???????. ??????? ??????? ??????? ????????-??????????, ??????????? ????? ? ?????????. ?????? ? ????? ???? ?????????!
?????? ?????? ?????? https://pic4you.ru ?????? ? ????????? ???????????? ? ????????. ????? ?????, ????? ???????????? ? ??????????, ??????? ? ???????. ???????? ??????? ???????????? ?????? ??? ?????? ??????.
???????? ???????? https://moidomiks.ru ?????? ?????? — ????, ?????? ? ????????? ?????????? ??? ???? ? ????????. ?????, ???????, ?????????? ? ????????? ??????. ???????? ??????? ?????? ? ???????? ???????????? ??? ?????? ??????.
ideainnovationlab – A creative space for experimenting with advanced concepts.
??????? ?????? https://casinos.ceo ?????? 2025 — ?????????? ????? ???????? ? ?????????, ?????? ? ?????????. ????????? ???????, ???????? ??????, ???????? ?????? ? ?????????. ???????? ??????? ???????? ?????? ?? ?????? ?????? ? ?????????.
???? ?????? ??????????? ? ???? ?????? – ?????? ??? ? ?????????????? ???? ???????? ???. ??????? ??????????? ???????? ????? ????????? ????? ? ??????? ???????????? ?????? ??????????.
???, ??? ????? ???????????? ? ?????????????, ???????? ?????????? ?????????? ?? ????????????? ??????: ??? ?????? ????????? ????? ? ????, ?? ??????? ????? ? ?????? ???????? ??? ?????? ??? ?????????. ?? ???????? https://www.florion.ru/catalog/novogodnie-kompozicii-iz-iskusstvennyh-cvetov ????????-???????? «???????» ??????? ???????? ???????? ??? ????, ?????, ??????? ??? ??????????? ???????? — ?? ?????????? ??????????? ?????????? ?? ???????????? ?????????? ???????. ????? ????? ?????? ??????? ? ???????????? ?? ???? ? ???, ???????? ?????????? ????????? ?????????? ????? ?????? ????????????.
impactcollective – Turns shared ideas into positive, measurable results.
????? ?????????? ????????? ??? ?????????? ?? Windows? ???????? https://pcutilites.com/ – ?? ??????? ??????? ??????? ???????? ? ?????????? ????????? ???? ????????? ???????? ??? ????????? Windows. ???????? ? ??????? – ??? ??? ????????? ??? ???????, ????, ?????, ??? ??????????? ? ???????. ????? ? ??? ???? ?????? ? ????????? ????????, ? ????? ?? ????????. ????????? ?? ?????.
Read More: https://theweekly-horoscope.com/horoscope-for-people-born-on-june-25/
step forward learning – Encourages taking actionable steps after understanding key concepts.
?????? ?????? ???????????
mattersfirst – Helps you sort priorities and keep attention on what’s really important.
explore imagination and intelligence – The content inspires combining creative thought with smart solutions.
?????????? ?????? ?????? — ??? ?? ?????? ??????
https://dreamproperties.site/author/kendra5846431/
life chapter tips – The platform offers guidance for moving into new life phases.
decisionnavigator – Provides tips to approach decisions logically and effectively.
stepbystepaction – Makes it easy to move forward with structured actions.
momentumboost – Helps generate immediate momentum for effective action and results.
????? ???????? ??? ??????? ???????? ???????? ???? Zipin https://zipin.ru/ – ? ??? ? ??????? ????? 1500 ????????? ?? ??????? ?????????????? ? ?????????, ??? ????????? ??????? ???????. ?????????? ??? ??????? – ??? ?? ??????? ??? ??????????? ??? ???????. ??? ????????????? ????????? ????????????????? ?????? ? ??????? ?????????.
forwardmotionplanner – Helps users create steady movement toward goals with actionable steps.
?????? ?????? ?????? https://pic4you.ru ?????? ? ????????? ???????????? ? ????????. ????? ?????, ????? ???????????? ? ??????????, ??????? ? ???????. ???????? ??????? ???????????? ?????? ??? ?????? ??????.
progress through learning – Focuses on turning knowledge into meaningful forward action.
successoutcomeguide – Guides users in creating results that are both positive and actionable.
???????? ???????? https://moidomiks.ru ?????? ?????? — ????, ?????? ? ????????? ?????????? ??? ???? ? ????????. ?????, ???????, ?????????? ? ????????? ??????. ???????? ??????? ?????? ? ???????? ???????????? ??? ?????? ??????.
Updated today: https://howheavyisit.com/animals/how-much-does-a-boar-weigh/
?????????? ????????????? ?????? — ???????? ???????
https://git.bp-web.app/tamerajad84324/2106909/wiki/tamozhennoe-oformlenie+43t.-
Artisanal Craft Collective – Beautiful handcrafted goods, navigation feels intuitive and pleasant.
innovativegrowthpaths – Encourages exploring innovative paths that foster consistent development.
essentialinsights – Provides tips to focus energy on the things that bring the most value.
innovative progress tips – The content shows ways to advance abilities and unlock new avenues.
new growth areas – The site emphasizes regions with high potential for development.
?????? ????? ?????? ??????, ?? ????? ???????? ??????????? ?????? ?????? ? ??????? ?????. ?????? ?????? ?????? ?? ?????? ?????????? ????? ??????????? ?????. ????? ?????? ??????? http://topovye-kazino-onlajn.biz.ua/ ? ?????????? ?????? ??????. ?????? ? ?????? ?????? ????? ????? ????????? ????????? ??????.
?????? ?????? ? ??????? ????? ??? ???????? — ????????, ?? ??? ????.
?????? ?????? ???????????? ?????????? ??? ?????? ????. ?????? ?????? ? ?????????? ???????? ?????. ?????? ?????? ??? 10 ??????????? ?? ??????? ???????. ?????? ?????? ??????? ?????? ???????? ???????? ???????.
innovationseeds – Helps plant the seeds for future innovation.
prospectpath – Highlights actionable paths to seize opportunities quickly.
?? ????????? ???? ???????? ???? ????????
betterchoicesguide – Guides users to make informed decisions quickly and efficiently.
?????????? ?????? ?????? ?????? ?????? ? ???, ?????????
https://git.poggerer.xyz/bbbgemma633163
step-by-step learning – Encourages learning skills in small steps while building real projects.
corefoundationsnavigator – Helps users build reliable groundwork for long-term achievements.
melbet ???????????? melbet ???????????? .
progressflowhub – Helps maintain continuous momentum for efficient goal achievement.
?????? ??? ?????? ? ?????? ???????? ?????? ??? ?????? ? ?????? ???????? .
successpathfinder – Helps identify the first actions to start moving toward success today.
successpathhub – Inspires creating results-oriented actions for tangible success.
achieve meaningful outcomes – It emphasizes practical approaches to get impactful results.
progress through creativity – The approach encourages experimentation and thoughtful growth.
?????? ??????????? ???? ??? ?????? https://fen-dn-kupit-1.ru/ .
growthandopportunityhub – Helps identify paths that combine growth and strategic opportunities.
startnowguide – Encourages starting now instead of waiting for the perfect time.
?????????? ?????????? ???????????? ?????? — ????????? ? ???????
https://gitea.chloefontenot.org/ivoryhobart28
future-ready growth – Focuses on growth ideas designed for long-term success.
energypathfinder – Offers guidance to sustain motivation and drive projects forward.
systematicgrowthguide – Encourages creating repeatable processes for continuous improvement.
potentialnavigator – Guides exploration of paths that maximize personal and professional growth.
Erotica
ideaimpactengine – Helps users learn and convert ideas into successful outcomes in projects.
<enhance core strengths – It shows practical ways to apply key abilities for better results.
opportunitypotentialhub – Inspires exploring hidden opportunities to achieve measurable growth.
focused action plan – The content shows how to align effort with desired outcomes.
?????????? ?????????????? ?????? ??? ?????? ??????
https://glamourrealestate.online/author/homergrullon98/
clarityinaction – Brings clarity and focus to every step you take.
scalable innovation tips – Provides guidance for innovative ideas that can expand responsibly.
strategicclarityguide – Helps build strategic clarity for achieving focused growth and measurable outcomes.
????? ?????? ????? ?????? .
?????? ?????? ??????? ?? ??????? ?????? ?????? ??????? ?? ??????? .
?????? ?????? .
opportunityhubnow – Encourages discovering and acting on opportunities without delay.
essentialpathways – Shows ways to streamline focus and avoid distractions from trivial matters.
????????? melbet ????????? melbet .
scalabilityinsights – Inspires exploring channels and strategies that maximize expansion.
create growth systems – This platform provides strategies for building systems that ensure steady progress.
strategic growth ideas – The focus is on structured approaches to advance intentionally.
?????????? ??????? ?????? ?????? ?? ??????
https://karabass.pro/@shanicecoxen82?page=about
????? ?????????????? ???????? https://www.shkola-onlajn1.ru .
zoneinsightengine – Inspires identifying promising opportunity zones and maximizing growth potential.
learningactionhub – Provides a platform to combine learning and practical execution.
wisestepsoptimizer – Helps structure stepwise growth for long-term success and measurable outcomes.
real-life learning – Highlights lessons and skills gained through practical application and observation.
??????? ?????? ?? ????? ?????? ??????? ?????? ?? ????? ?????? .
dyson com ??????????? ???? https://www.fen-dn-kupit-3.ru .
?????????? ?????????? ??????????? ?????? — ??? ?????
https://manazelgulf.com/author/estellamorris5/
Modern Essentials Hub – Essentials collection feels curated, browsing is quick and smooth.
kickstart your day – It highlights strategies for making a strong and effective start.
foundational growth tips – It emphasizes building a stable base for personal and professional achievement.
sustained momentum – Highlights ways to maintain consistent forward movement toward goals.
clearmindstart – Helps start thinking clearly to improve decision-making and focus.
futurefocusguide – Provides tips for planning ahead and achieving lasting success.
creativeclarity – Focuses on gaining clarity through new ways of thinking.
???????? ?? ?????????? ????? ???????????? ?????????? ??????????????? ???????? ?????????? ?????? ?? ?????????? ??????????. ?? ????? https://dizaynland.ru/ ???????????? ??????? ??????? ??? ???????? ????????????????? ?????, ??????????????? ?????????? ? ??????? ? ????????????? ?????????? ????????. ??????????? ????????????? ?????????????? ??????? ? ?????? ???????????? ???????, ??????? ? ????????? ?????????, ????????? ??????????? ?????? ???????? ? ???????????? ????????? ??? ???????????? ??????????.
motionnavigator – Helps users maintain steady progress and forward energy toward goals.
?????? ????? ??????????? ?????? ????????
phaseforwardguide – Helps users advance into the next stage of work with focus and intent.
????? ???????? ??????????? ???????? ?????? ??????? ????????? ??????, ????, ????, ?????? ???????? ? ???????? ??????. ???????? ??????? ???????? ??????????? ???????? ??? ???? ??? ???????.
discover alternative paths – Encourages considering new approaches to achieve goals effectively.
impactnavigator – Encourages creating a structured roadmap for successful and meaningful outcomes.
Szukasz kasyna? kasyno online blik sprawdzamy licencje, metody platnosci, czas realizacji transakcji i dostepnosc gier. Praktyczne informacje o kasynach z platnoscia BLIK.
?????????? ?????? ??? ??????? ????????
https://ninetylayersreal.com/author/lienlester6831/
decision clarity tips – It helps break down choices into manageable steps.
???????? ?? ?????? ??? ??????????? ???????? ?? ?????? ??? ??????????? .
impact success guide – The platform shows ways to achieve strong outcomes with smart strategies.
discovernewgrowth – Encourages discovering new ways to expand effectively.
creativemindpaths – Offers ideas to explore unconventional routes and achieve innovative outcomes.
?????? ????? ?????? ????? .
??????? ?????? ?????? ?? ??????? ??????? ?????? ?????? ?? ??????? .
learningpathfinder – Provides insights to keep learning and advance steadily toward objectives.
optimization strategies hub – Focuses on practical approaches to improve processes effectively.
?????????? ?????????? ?????? ?????? — ????? ?????? ????
https://property.cbaservices.id/author/kengoddard9738/
startgrowingfast – Motivates starting rapid growth by taking focused actions today.
growthoptimizer – Guides users to make decisions that maximize growth and personal development.
decisionnavigatorpro – Helps users leverage hidden insights to take smart and impactful actions.
Content visibility improves when you buy tiktok likes strategically. Quality providers deliver engagement from genuine users rather than bot networks ensuring compliance with platform guidelines and sustainable growth metrics.
Lifestyle Picks Hub – Fast site performance with clean layout and easy exploration of products.
clarity and focus hub – It emphasizes maintaining attention and improving productivity.
forwardmomentum – Ensures steady advancement in both professional and personal projects.
????????????? ?????? ??? ????? ?????? ????????????? ?????? ? ??????: ?????? ??????? 55-86 ?????? ? ??????. ???????? ???? ??????????? ?????????????.
???????? ? ?????? https://kvartira-spb-pokupka.ru ??? ??????? — ??????? ????? ???????? ? ?????? ??????? ??????. ??????????? ? ????????? ?????, ?????? ? ????????, ??????????? ????????????? ? ?????????? ??????????? ?? ????????????? ? ????????????.
possibilitynavigator – Shows practical ways to explore opportunities and make forward progress.
knowledgeaccelerator – Helps users expand understanding and implement it for practical benefits.
?????????? ??????? ?????? — ????? ? ??????
https://saleproperty.net/author/jerrodbancks56/
direction discovery strategies – Offers methods to find effective paths for personal or professional growth.
melbet ???????? ??? ??????????? melbet ???????? ??? ??????????? .
opportunityfinderpro – Inspires users to locate new flows of opportunity and maximize results efficiently.
???????? ????? ? ????????? http://www.shkola-onlajn1.ru/ .
https://cap-games.jp/ ????????SEKIRO?DARK SOULS?FINAL FANTASY?Bloodborne ??????????????????????????????????????????????
interactivepracticehub – Encourages applying learned ideas practically to generate creative results.
Refined Everyday Picks – Items shipped promptly, packaging careful, overall a smooth experience.
habitformationhub – Guides forming habits that create long-lasting positive change.
???????? ? ????????? https://kupikvartiru-piter.ru ??????? ?????? ??????? ????? ??? ???????. ??????????? ? ??????? ???????, ?????????? ???????, ????????????? ???? ? ?????? ? ?????????? ??????????. ?????? ????????? ??? ???? ???????????.
????????????? ???????? ??? ?????????????? ????????? ? ???????? ????????? ????????. ????????????? ?????????? ?????????? ? ??????. ?????? ???????, ??????? ??????? ? ?????. ????????? ??????? ???????????? ????? ??? ??????. ???????? ?????? ? ?????????? ?????????: ????????? ?????? ?????????? ????????
learn and advance – This site provides practical learning to confidently improve your skills.
quicklearninghub – Offers resources to learn efficiently and apply knowledge fast.
????????????? ?????? ???????? ????????????? ?????? 65 ?????? ?????????: ????? ?????????? ?????? ??????? ? ??????????. ?????? ? ??????? ?? ??????. ???????? ????.
????? ????????? ?????????? ??? ????????????? ???? ? ????????? ??????? ?? ???? ???????? ???? https://stroi-garantiya.ru/ – ?? ?????? ?? ??????????????? ??? ???????? ???????. ?? ????? ?? ??????? ????????? ?????????? ?????????. ??? ????????????? ???????????? ? ?????? ????????. ? ??? ??????? ? ????????????? ????.
?????????? ?????????? ???????????? ?????? — ????????? ????????
https://tageeapp.com/@jewellhebert9?page=about
speed up learning – Direct and energetic, clearly promoting advancement.
strategicfocusstarter – Inspires users to launch initiatives with deliberate planning and direction.
???????? ? ?????? https://kvartira-spb-pokupka.ru ??? ??????? — ??????? ????? ???????? ? ?????? ??????? ??????. ??????????? ? ????????? ?????, ?????? ? ????????, ??????????? ????????????? ? ?????????? ??????????? ?? ????????????? ? ????????????.
directionfinder – Guides you to identify the most important next step effectively.
rapid results guide – Highlights straightforward methods to achieve impact efficiently.
newinsightshub – Helps users discover new perspectives that spark creativity and innovation.
focusedactionhub – Guides users to take intentional actions for consistent progress toward goals.
melbet ???????? melbet ???????? .
????????? ???????? https://kvartira-umetro.ru ??? ???????: ?????????? ???????????, ??????? ????? ?? ????, ?????? ? ???????. ?????? ????????? ?????????, ???????????? ???????????? ? ????????????? ??????.
Artful Daily Hub – Daily curated selections, browsing feels smooth and engaging.
clear step growth tips – It provides advice for taking practical, deliberate steps.
???????? ? ????????? https://kupikvartiru-piter.ru ??????? ?????? ??????? ????? ??? ???????. ??????????? ? ??????? ???????, ?????????? ???????, ????????????? ???? ? ?????? ? ?????????? ??????????. ?????? ????????? ??? ???? ???????????.
?????????? ?????????? ??????????? ?????? — ??? ???????
https://urlllll.com/crystlelockard
growthstrategyengine – Helps uncover practical strategies for achieving consistent growth.
learningnavigator – Guides users to refine strategies and adapt to challenges efficiently.
????? ??? ??? ?????? ? ?????? ??????, ????? ??????? ??????? ?????? ??????. ?????? ? ??????? ????? — ???????? ?????? ??? ???, ??? ?????? ?? ???????? ??????. ????? ??????? ????????? ????? ?????????? ???????, ???????? ??????? ?????? ??????. ??? ?????? ??? ???????? ?????????. ?????? ?????? ??????? ?????? ??????????? ????? ?????? ?????.
??????????? ?????? ?????? ?????? ????? ??????????? ????.
????? ?????????? ?????? ?????? ?????? ?? ?????. ?????? ?????? ??? ???????? ????? ???????? ????????. ?????? ?????? ? ??????? ????? ??? ??????? — ????????. ?????? ?????? — ??, ??????? ??????? ??????.
??????? ???????????? ?? ???????? ???????????
???????? ??? ???????? ????????
?????? ?????? http://roads.ru/main/promo-materialy/kak-vybrat-pesok-i-shheben-rukovodstvo-dlya-stroitelnyx-rabot/ .
intentional growth – Encourages personal and professional growth through purpose-driven actions.
???????? ?? ??????????? https://kvartiravgorod.ru ??????? ???????? ??? ????????. ??????????? ?? ?????? ??????? ??????????, ??????????? ??????????, ?????? ? ???????? ? ????????????? ?????? ?? ?????? ?? ????????? ??????.
clearobjectiveplanner – Helps organize the first steps with clarity and defined outcomes.
growthwithpurpose – Encourages deliberate actions that foster steady and intentional progress.
continuousgrowthnavigator – Guides building momentum gradually while learning to achieve steady results.
?????? ???????????? ??????? ?????? ???????????? ??????? .
?????? ?? ???? ????????? ????????????
???????? ??? ???????? ????????
?????????? ????????? ??????? ?????? — ??? ???????
https://worship.com.ng/kirstenpratt17
strategic growth path – The content provides clear directions for moving forward effectively.
????????? ???????? https://kvartira-umetro.ru ??? ???????: ?????????? ???????????, ??????? ????? ?? ????, ?????? ? ???????. ?????? ????????? ?????????, ???????????? ???????????? ? ????????????? ??????.
?????? ????? ??? ????? http://www.shkola-onlajn2.ru .
accelerated learning zone – Inviting and motivating, clearly centered on progress.
potentialahead – Inspires thinking beyond today to shape lasting results.
???????? ?? ??????????? https://kvartiravgorod.ru ??????? ???????? ??? ????????. ??????????? ?? ?????? ??????? ??????????, ??????????? ??????????, ?????? ? ???????? ? ????????????? ?????? ?? ?????? ?? ????????? ??????.
?????????????? — ?????????????? ?????????
??????? ??????
GK88bet, not bad, I signed up for a friend, he said the odds are good and also got some win, but be careful. You can read more at gk88bet.
momentumpathfinder – Guides users in designing a path that sustains progress and focus.
moveaheadlearn – Guides learning consistently while taking confident steps forward.
?????????? ???????????? ????????? ?????? ? ???? ??????? ???????? ??????? ??????????. ??? ???????? ???????, ??????? ??????????, ?????? ??? ????? ? ?????. ??????? ??????? ? ?????????. ???????? ????????? ????? ? ? ????. ??????? ????????????? ????? ???? ????: ????? ??????? ??????
???????? ????? ????????? ??????? ? ???? ??????? ???????? ????????????????? ???????. ??????? ?????????? ????????????, ???????? ?????? ? ?????? ???????????. ?????? ?????? ? ??????????? ??? ????????. ????? ????????? ?????????. ???????? ?????? ? ???????????? ????????? ? ??????? – ?????? ???????? ? ??????
progresslearner – Guides learning and steady advancement for professional and personal development.
resultsdrivennavigator – Encourages implementing growth approaches that deliver practical and effective outcomes.
????????????? ???????? https://kvartiradlyazhizni.ru ? ?????? ??? ???????. ??????? ????? ????????? ? ?????? ??????? ??????, ??????? ????? ?? ???? ? ??????????. ???????????? ????????????, ?????? ? ???????? ? ?????????? ?????????? ??????.
?????? ???????? ?????? ????????, ????? ????????? ??????? ? ???????. ??????? ?????????, ??????????? ?? ?????????? ? ?? ????????. ??????????? ?????????????? ??????????? ? ???????. ????? ????????? ?????? ?????????? ?????. ?????? ?????????? ?? ?????? ??? ???? ????????? ?????????? – ????? ?? ?????? ?? ????? ??????
speedyresults – Quick methods to build value and advance your goals today.
?????????? ??????? ?????? ?????? ??? ??????? ??????, ?????????????
https://www.property.aygodam.com/author/mdgdemetrius6/
????????? ????????????? ?????? ?????? ????????????? ????? ?????????: ???????? ????????????? ????? ? ?????????. ???????? ??????????? ??? ????????? ???????????.
discover winning ideas – This site is a great spot for finding smart and creative approaches.
learningexpander – Focuses on expanding knowledge and scaling progress.
creativevisionhub – Helps users generate fresh ideas and adopt novel approaches to problem-solving.
?????? ????????? ?????? ????????? .
???????? ?? ??????????? https://kvartiravgorod.ru ??????? ???????? ??? ????????. ??????????? ?? ?????? ??????? ??????????, ??????????? ??????????, ?????? ? ???????? ? ????????????? ?????? ?? ?????? ?? ????????? ??????.
?????????? ????? ?????? ????? ???????? ???????
https://damalist.com/author/leladoolan954/
ideafinderpro – Guides discovering fresh ideas and implementing them effectively.
innovationpathfinder – Helps unlock creative potential and develop innovative solutions consistently.
startpurposefully – Encourages beginning tasks with focus and intentional goals.
growth path learning – Structured well and easy to understand, providing natural guidance.
melbet ???? ??????? melbet ???? ??????? .
????????????? ???????? https://kvartiradlyazhizni.ru ? ?????? ??? ???????. ??????? ????? ????????? ? ?????? ??????? ??????, ??????? ????? ?? ???? ? ??????????. ???????????? ????????????, ?????? ? ???????? ? ?????????? ?????????? ??????.
???????? ????? ? ????????? https://shkola-onlajn1.ru .
practical progress tips – The guidance is grounded in steps that work in real life.
???????? ???? https://sezon-podarkov.ru/catalog/biznes-podarki-s-logotipom ? ?? ??????? ???????? ? ?????? ????????????? ??????? ? ??????-???????? ? ?????????. ?????????? ??? ??????????? – ?? ????? ???????, ? ???? ????????! ???????? ? ???????????? ? ??????????? ??????, ? ???????? ?? ?????? ??? ???????? ? ????????? ??????. ??? ??????? ??????? – ?? ????? ???????? ???? ? ?????????? ???????? ? ?????????.
Paris sportifs Website : matchs, tournois, cotes et resultats, lignes de paris et evenements en direct. Presentation detaillee des fonctionnalites et du fonctionnement du service.
Envie de parier? website here Service de paris sportifs et footballistiques. Presentation des evenements disponibles, des cotes, du mode direct et des principales fonctionnalites de la plateforme. Informations utiles pour les utilisateurs.
growthfastlane – Guides individuals to grow quickly with consistent competence.
?????? ????? ?????? ??????, ?? ????? ???????? ??????????? ?????? ?????? ? ??????? ?????. ?????? ?????? ??????? ???????? ??????, ??? ??????? ??????. ?????? ?????? ?????? ?? https://topovye-kazino-onlajn.biz.ua ? ???????? ??????????. ?????? ?????? ??????? ?????? ??????????? ????? ?????? ?????.
??????????? ?????? ??????? ?????? ???????? ?????????.
?????? ?????? ??? ??????? ?????? ???????????? ??? ??????? ???????. ?????? ??? 10 ?????? ???????? ??????????? ??????. ?????? ?????? ? ??????? ????? ??? ??????? — ????????. ??????? ?????? ?????? ??????? ???? ??????? ???????.
growthengine – Inspires building skills and capabilities through consistent practice and planning.
?????? ??????????? ??????? ?????? ???? ?????? ??????
https://ghurairproperties.com/agents/coreyworthy506/
?????? ???????????? ????? https://www.roads.ru/main/promo-materialy/kak-vybrat-pesok-i-shheben-rukovodstvo-dlya-stroitelnyx-rabot/ .
?????? ?????? ?? ??????????? ?????? ?????? ?? ??????????? .
strategic approach ideas – The content highlights methods for careful and deliberate planning.
effectivepracticestools – Helps users discover effective practices for achieving their goals efficiently.
?????? ????? http://www.shkola-onlajn2.ru/ .
Paris sportifs telecharger 1xbet : matchs, tournois, cotes et resultats, lignes de paris et evenements en direct. Presentation detaillee des fonctionnalites et du fonctionnement du service.
Envie de parier? find out here Service de paris sportifs et footballistiques. Presentation des evenements disponibles, des cotes, du mode direct et des principales fonctionnalites de la plateforme. Informations utiles pour les utilisateurs.
Click Ping Collective – Excellent selection, fast shipping and responsive customer assistance.
ideaintelligence – Builds stronger ideas through deep understanding.
???????? ??????????? — ?????????? ?????????? ? ??????????? ?????? ??? ????????
https://git.kokscharow.ru/kelleefossey69
progress building space – Feels approachable and centered on long-term consistency.
quick learning hub – Encourages fast adaptation with clear and actionable advice.
stepbystepstarter – Inspires users to begin growth with actionable steps and practical planning.
Plateforme en ligne their website paris sportifs, matchs de football, evenements en direct et statistiques. Decouvrez les fonctionnalites du service, les marches disponibles et comment l’utiliser.
unlock your uniqueness – Engaging and approachable, with a focus on personal distinction.
???????? ?? ??????????? https://kvartirav-vygodno.ru ???????? — ?????????? ???? ? ????? ??????????. ?????? ?? ??????????, ?????? ? ???????????, ???????? ? ??????????. ?????????? ??????? ? ????????????? ??????.
growth methodology guide – Inspires users to create well-organized paths for advancement.
???????? ????? ????????? ??????? ? ???? ??????? ???????? ????????????????? ???????. ??????? ?????????? ????????????, ???????? ?????? ? ?????? ???????????. ?????? ?????? ? ??????????? ??? ????????. ????? ????????? ?????????. ???????? ?????? ? ???????????? ????????? ? ???????: ?????? ??????? ????
consistent progress mindset – It encourages steady improvement that feels natural.
fasttrackprogress.click – Encourages timely efforts and taking steps that create real results.
modastore.shop – Modern collections, navigating the site is easy and product presentation is clear.
?????????? ?????????????? ?????? ??? ?????? ??????
https://git.wantbug.com/jacintodelgadi
growthjourneyguide – Provides a structured approach to taking actionable steps.
shopfinderhub.shop – Items displayed clearly, browsing is easy and finding bargains is fun.
focusedactionengine – Encourages taking consistent steps to maintain momentum and achieve goals.
luxurycuration.click – Curated collection, platform presents items attractively with a premium feel.
strategicroadmap – Guides creating actionable steps that lead to real-world results.
designimpactclick.shop – Insightful content, helps users build structured plans for impactful outcomes.
strategic growth hub – Supports organized thinking and actionable planning for progress.
Plateforme en ligne this page paris sportifs, matchs de football, evenements en direct et statistiques. Decouvrez les fonctionnalites du service, les marches disponibles et comment l’utiliser.
???????? ?? ??????????? https://kvartirav-vygodno.ru ???????? — ?????????? ???? ? ????? ??????????. ?????? ?? ??????????, ?????? ? ???????????, ???????? ? ??????????. ?????????? ??????? ? ????????????? ??????.
goalpathfinder.click – Practical guidance, helps uncover key personal goals and make deliberate progress today.
measured progress path – Encourages balance and steady forward movement.
Global Essentials Picks Hub – Well-curated selections with smooth flow and impressive quality.
????????? https://seoprofi.org/ ????????????? ?????? ?? ???????? ?????????? ??? Rutube ? VK ?????, ? ????? ?????????? ???????????? ?????? ??????????? ????????. ??????? ??????????? ?????????? ?????????? ??????????? ? ?????????? 50-80%, ??????????? ?????? ??????????? ? ????? ????? ?? 1-3 ????. ??????? ?????? ???????? ?? 1200 ?????? ?? 1000 ??????, ??????? ????????? ????????? ???????? ? ?????????? ?????????????? ????????? ??? ???????????? ??????????? ???????? ? ????????????? ? ????????? ??????.
personal growth strategies – The platform provides tips to make transformation accessible and realistic.
?????????? ????????? ??????? ?????? — ????? ????
https://gitea.tecamino.com/brendannvl8927
direction discovery – A calm and positive approach to looking ahead.
actionboost.click – Encourages immediate steps and keeps momentum high for personal growth.
stylehub.shop – Stylish selections, shopping feels easy and the product display is attractive.
marketfinds.shop – Smooth shopping, platform helps users explore a range of products and offers.
valueexplorer – Makes discovering hidden opportunities smooth and efficient.
strategicimpactclick.shop – Practical platform, encourages structured planning for consistent, meaningful outcomes.
luxuryselectionhub.click – Refined platform, displays curated items elegantly with a polished browsing experience.
innovationquest – Encourages exploring challenges that inspire creativity and problem-solving.
daily focus navigator – Motivates prioritizing meaningful tasks and consistent improvement.
purposejourneyclick.click – Motivational content, encourages exploring inner goals and achieving clarity for effective planning.
casino online games casino online games .
Green Living Marketplace – Smooth shopping experience with sustainable products clearly displayed.
????? ??? ????? http://www.shkola-onlajn1.ru .
growth strategy with purpose – Clear and inspiring, promoting deliberate and focused efforts.
??????? ?????? ?????? — ?????? ? ???????
https://impactrealtygroup.net/author/holleymidgett7/
start fresh direction – The concept is invigorating and offers clear guidance for moving forward.
Cheat Empire — ??? ????????? ?????? ? ???????? ??????????? ? ??????? ?????: Roblox (???????), Genshin Impact (?????? ??????), Standoff 2 (???????? 2), PUBG Mobile (???? ??????), Counter-Strike 2 (?? 2) ? ?????? ??????. ????? ?? ??????? ??????????? ????, ??????? ? ???? ??? ???????, ????? ?? ???????????, ??????? ?????????? ? ?????? ??? ????????. ??? ????????? ????????? ? ????????? ??? ??????????. ?????????? ??? ????????! https://cheat-empire.fun/
???????? ???????? https://shkola-onlajn2.ru/ .
trendspot.shop – Trendy products showcased clearly, navigation feels smooth and hassle-free.
results focus guide – Offers practical tips for taking actions that maximize efficiency and impact.
????????????? ?????? ??? ????? ? ???????? ??????????? ??????????? ???? ? ????????. ?????? ??????, ??? ????????, ?????? ??????? ?????. ???????? ??????? ????? ?????? ?????????? ?????. ???????? ???? ??????? ? ???????. ???????? ?????? ???????????? – ?????? ??????? ????????
discovercreativepaths.shop – Inspiring content, encourages exploring new ideas and approaching challenges creatively.
smartcart.shop – Straightforward interface, buying products feels seamless and convenient.
https://tanoshikoto.net/ ?????????????????????????????????????????????????????????????????????????????????????????
growthpathnavigator – Inspires establishing progress that continues efficiently over the long term.
growthstepsclick.shop – Inspiring platform, site supports consistent action for meaningful progress.
new growth concepts – Encourages experimentation and discovery of effective growth methods.
discoveryourpurpose.shop – Insightful platform, encourages exploring personal intentions and meaningful objectives clearly today.
Curated Goods Marketplace – Items feel carefully chosen, browsing is smooth and pleasant.
???? ??????????? ???????, ??? ? ??????, ?????????? ???? ??????
https://linkqb.com/pWTjy
potential explorer – A concise phrase that feels optimistic and open-minded.
????? ?????? ????? ?????? ? ??? ?????? ??????????, ?????? ??????? ??????-?????? «????-?????» ???????? ????? ?????????? ??????????? ?? ????????? ??????. ?? ????? https://zaym-agent.ru/ ?????? ?????????? ??????? ??? ?????? ? ????????? ?? ??, ??? ????? ???????? ???? ?? ????? ?????????????, ? ??????????? ??????? ?????????? ? ??????????? ?????????. ??????? ???????, ???????? ???????? ? ?????? ?? ??????????? ???????????? ????????? ????????????? ????????? ??????? ??????? ? ?????????? ?????????? ?, ??? ?????????????, ? ??????? ??????? ??? ????? ????????.
refresh your methods – Simple and motivating, promoting fresh ways to improve outcomes.
Le site web 1xbet apk propose des informations sur les paris sportifs, les cotes et les evenements en direct. Football, tournois populaires, cotes et statistiques y sont presentes. Ce site est ideal pour se familiariser avec les fonctionnalites de la plateforme.
acttodayhub.shop – Inspiring content, site helps users act immediately and make impactful choices.
goalpathhub.shop – Clear guidance, site encourages users to create actionable steps and follow them confidently.
momentumflow.click – Great suggestions for staying active and moving toward goals quickly.
simplebuyzone.shop – Convenient and straightforward, shopping experience is smooth and enjoyable.
execution momentum – Encourages keeping actions aligned over time.
???????? «?????? ??????» ?????????? ??????? ??????? ??????? ??????????? ???????????? ????????? ???????? ?? ???????? ?????. ??????? ???????????????? ?? ??????? ??????????, ????????? ? ????????? ?????, ????????, ??????????? ? ????????? ?????. ????????? spc ???????? ?? ????? mr-parquet.ru ???????????? ????????? ??????? ?????????????? ? ?????????? ?????????? ? ????????????. ??????? ???????? ?????????? ????????????, ?????? ??????? ? ??????????????? ? ???????? ???????. ?????????? ?????????? ? ?????? ???????????? ??????? ????????? ?? ??????? ?????????????? ??????????.
impactguidancehub.shop – Practical site, helps users follow actionable steps for tangible progress.
momentum growth platform – Offers strategies for continuous progress without burnout.
?????? ?? ?????? — ?????????? ?????????? ?????? ?????? ?????? ??????
https://myafritube.com/@adrienepedder?page=about
Envie de parier 1xbet rdc est une plateforme de paris sportifs en ligne pour la Republique democratique du Congo. Football et autres sports, paris en direct et d’avant-match, cotes, resultats et statistiques. Presentation des fonctionnalites du service.
freshideaexplorer.shop – Insightful platform, inspires users to uncover creative ideas and explore opportunities.
sykaaa ??????????? ???? ?????
https://infolenta.com.ua/khto-taki-kompaniytsi-istoriia-ta-tradytsii-ukrainskoho-narodnoho-huliannia/
Gibddinfo.ru — ??? SEO-????? ??? ???????????? ? ?????????? ?????????????, ??? ????? ???????? ????????? ???????????, ?????????? ?????? ?????? ? ?????????? ????????? ? ????? ?????? ?? ???????????? ???????. ????????? ??????? ??? ???????? ???, ????????? ? ?????? ???????, ??? ?????? ?? ??????? ????????? ??? ????????????????? ?????. ?????????????? ? ?????????? ? ?????? ?????????? ????? ?? https://gibddinfo.ru/ — ????? ?????????? ??, ??? ????? ???????? ??????, ?????????? ?????? ? ????? ???????? ?????? ??????????? ? ??????? ????????? ??????????? ? ????????-??????????.
Eco Lifestyle Marketplace – Smooth interface with well-structured product categories and clean visuals.
????? ??????????? ???????? ??? ?????????? ?????????? ? ??????, ??? ? ???? ?????? https://doskadonbassa.ru/ ?????????? ?????????? ?????????? ? ?????????? ????-????, ????????????, ?????? ? ??????. ??????? ????????? ???????? ?????????? ?????????? ?????????? ? ????????? ? ????????????????? ????????????. ????????? ??????????? ?????? ?????????????? ?????????? ?????? ??? ?????????????? ????????. ??????? ??????????? ? ?????????? ?????????? ???????? ??????? ???????????? ?????????? ?????????!
growthpathshub.click – Practical insights, site helps users identify actionable steps for consistent growth.
focused growth hub – Layout is intuitive, reinforcing productive planning.
connectandshare.click – Users share concepts easily, site encourages imagination and group collaboration.
Amazing issues here. I am very happy to look your post. Thanks a lot and I’m taking a look ahead to touch you. Will you kindly drop me a e-mail?
zoo animal pornosu
purposeful vision guide – Calm and structured, helping users feel guided.
?????????? ?????????? ?????? — ??????, ???????????, ????????
https://playidy.com/@sheilafrasier?page=about
newhorizon.shop – Great variety, site inspires discovering fresh products and innovative trends easily.
a href=”https://discoveropportunityspace.click/” />potential navigator – Inspires uncovering fresh options and future opportunities.
stepbyintent.shop – Focused hub, site highlights deliberate moves and consistent efforts for growth.
strong start guide – Encourages taking decisive early steps and keeping progress steady.
???????? ?? ??????????? https://tltdomik.ru ??????? ? ???????????? ?? ?????????? ????????. ??????????? ??????????, ?????? ?????? ??????????, ?????? ? ???????? ? ??????????. ???????????? ?????? ?? ?????? ?? ????????? ??????.
???????? ? ???????????? https://tltnewflat24.ru ? ?? ????????? ????? — ??????? ????? ????????. ?????? ?????? ? ???????, ?????? ??? ???? ??????, ???????????? ???????????? ? ??????????? ????????????? ???????.
deepthoughtclick.click – Motivational platform, supports exploring topics in depth and improving critical thinking skills.
Unique Goods Hub – Carefully curated items that make browsing enjoyable and memorable.
better results hub – Straightforward messaging that motivates improvement with ease.
momentumboost.shop – Motivational site, helps users maintain energy and stay on track with progress.
knowledgecenter.click – Insightful and practical, platform delivers valuable tips for growth and development.
smart growth plans – Encourages efficiency and clear, strategic steps.
?????????? ?????????? ??????????? ?????? ?????? ? ??? ????????
https://realtyzone.com.au/author/clarafranki861/
learnandadvance.click – Insightful hub, content helps users gain knowledge quickly and make measurable progress.
????????????? ???????? ??????????? https://shkola-onlajn2.ru .
explore fresh concepts – Offers a new perspective and encourages innovative thinking in daily tasks.
adventurestore.shop – Great variety, site motivates checking out unique products easily.
advancementhub.click – Informative platform, guides users to explore growth paths and improve results systematically.
sustainable results guide – Encourages systematic effort and ongoing achievement over time.
Necessities Marketplace – Quick shipping, neat presentation, and very satisfied with my purchase.
???????? ?? ??????????? https://tltdomik.ru ??????? ? ???????????? ?? ?????????? ????????. ??????????? ??????????, ?????? ?????? ??????????, ?????? ? ???????? ? ??????????. ???????????? ?????? ?? ?????? ?? ????????? ??????.
???????? ? ???????????? https://tltnewflat24.ru ? ?? ????????? ????? — ??????? ????? ????????. ?????? ?????? ? ???????, ?????? ??? ???? ??????, ???????????? ???????????? ? ??????????? ????????????? ???????.
actionclarity.click – Motivational hub, guides users to clarify objectives and follow a clear plan for success.
vision alignment hub – The overall feel is grounded and purpose driven.
??????? ?????? ?????? — ??????, ???? ?????????
https://soundrecords.zamworg.com/frankverdon108
pathfinderhub.shop – Supportive platform, guides users in developing their goals and personal direction.
Online 1xbet rdc telecharger est une plateforme de paris sportifs en ligne. Championnats de football, cotes en direct et resultats sont disponibles. Page d’information sur le service et ses fonctionnalites pour les utilisateurs de la region.
goal clarity platform – A clean presentation that keeps attention on priorities.
https://infolenta.com.ua/chomu-bolyt-likot-osnovni-prychyny-boliu-ta-sposoby-likuvannia/
grow intention driven – Inspiring content, guiding users to grow with clear purpose and focus.
????????? ???????? ???? ????????
https://infolenta.com.ua/yak-diznatysia-sviy-taryfnyy-plan-kyivstar-5-sposobiv-pereviryty-aktyvnyy-taryf/
strategic learning guide – Offers insights for mastering skills before expanding initiatives.
growthactionplanner.shop – Motivational platform, inspires structured steps toward achieving meaningful outcomes effectively.
newclarityhub.click – Motivational content, site highlights prioritization and achieving clarity in everyday tasks.
?????? ? https://shkola-onlajn5.ru/ .
streetstylehub.shop – Stylish items, site gives an urban, contemporary feel for shoppers.
??????? ??????? ?????????????, ????? ????????? ?????? ???????. ??????? ??????? ? ?????????? ????, ???????? ??? ????? ???????????? ????. ??? ???????? ?????? — ???? ??? ??? ????????? ? ????? ?????.
???????? ???????? ??????? ???? ????????? ??? ?????????? ???????. ???????????? ??????? ???????????? ?????????? ??????. ???????? ??? ??? ??????? ????????, ??? ? ??? ????????. ?? ??????, ??? ????? ????? ????????? ???????. ???????????, ??? ??? ??????? ???? ??? ???????. ??????? ????? ??? ???, ??? ??????????? ???? ???. ???????? ? ?????????? ????? ????????? ?? ??????????.
???????? ??????? ?? ????? ?????? ???????? ??????? ?? ????? ?????? .
?????? https://natyazhnye-potolki-samara-6.ru .
life purpose navigator – Inspires finding significance in daily actions and long-term goals.
??????? ???????? ?????? http://natyazhnye-potolki-samara-5.ru/ .
discoverhiddenroutes.shop – Insightful platform, encourages exploring alternative paths and new possibilities.
?????? ??????????? ??????? ?????? — ?????????? ???? ????????
https://truthtube.video/@aletheaa29268?page=about
???????? ???????????, ?????, ??? ??????? ????????????? ?? ??????????. ????? ???????? ???????? ?????? ?????? ??? ?????? ??????? zapchasti-dlya-motocikla.biz.ua. ??????? ???? ????????? ? ?????????? ?????????? ? ??????????????.
???????? ??? ????????? ??????? ????????, ??? ?????????. ?????????? ?????? ? ??????? ? ????????? ????????????. ??????? ???? ??????? ???????? ? ??????????? ?????????. ??????? ???????? ??????? ????????????? ??? ?????????? ???????. ???????? ??????? ??? ??????? ?????????????. ???????? ?? ???? ?????? ???????, ??? ??????. ??????? ????? ????????? ??? ????????? ?????? ?????.
explorepossibilities.shop – Motivating content, site encourages bold thinking and growth-oriented action.
Consistent Progress Hub – Supports building momentum through small, repeatable actions.
sykaaa ???????????
find growth opportunities – Well-structured and practical for identifying areas to advance.
workflow improvement hub – Focuses clearly on making operations work better over time.
thinking ahead hub – Casual and inviting, it still reflects forward momentum.
Mindful Growth Space – Helps users focus on key actions that lead to meaningful results.
plan your next move – Encourages thoughtful progression and clear direction for growth.
quicklearnhub.click – Practical insights, platform helps users acquire skills rapidly and efficiently.
thinkaheadhub.shop – Insightful content, encourages strategic foresight and well-informed decisions.
Modern Living Hub – Intuitive interface, fast pages, and an enjoyable shopping experience.
globalbuys.shop – Diverse products, platform makes international shopping effortless.
Speedy Learning Hub – Highlights practical steps to enhance skills and productivity quickly.
?????????? ?????? ?????? ?? ?????? ??????????? ??????????
https://volts.howto.co.ug/@virgilioirizar
thinkforwardnow.click – Insightful content, helps users generate innovative solutions efficiently and effectively.
quickdailyshop.shop – Great for everyday needs, platform is intuitive and convenient to use.
New Pathways Guide – Encourages exploring fresh directions for potential success.
Progress Lane Guide – Encourages choosing a pace that leads to consistent and confident progress.
classicfusiongoods.click – Beautifully curated items, platform merges heritage charm with contemporary trends.
Forward Growth Guide – Provides insight to plan growth with focus and measurable outcomes.
thinkclearlyhub.shop – Informative hub, supports users in analyzing situations and making confident decisions.
new directions guide – Motivates users to consider forward-looking strategies and possibilities.
?????????? ??????? ?????? ?????? ?? ??????
https://www.lescoconsdubassin.fr/agent/kandacemartel5/
navigate forward paths – Simple and encouraging, offering clarity for future directions.
Daily Necessities Hub – Fast shipping and well-packaged products made shopping easy and pleasant.
actioncenterhub.click – Motivating site, emphasizes executing plans promptly and staying focused on goals.
Learn, Apply, Optimize – Offers methods for fast learning paired with actionable improvements.
ideavisionshop.click – Encouraging platform, inspires innovative thinking and practical idea generation.
bestbargain.shop – Top savings showcased, browsing is quick and simple.
Explore Opportunities Hub – Offers guidance for uncovering valuable prospects and avenues.
optimized growth paths – Highlights efficiency and scalability in growth planning.
a href=”https://discoverinnovativethinking.click/” />Inspiration Stream – Delivers a steady flow of ideas that feel new and energizing.
lifestylezone.shop – Curated selections that feel contemporary and easy to navigate.
????????? ????? ????????? ????? .
premiumfinds.click – Unique and curated selections, navigation is easy and products stand out.
advancing growth track – Inspires progress while keeping the message clear and organized.
https://infolenta.com.ua/khto-taki-bilshovyky-prostymy-slovamy-istoriia-komunistychnoi-revoliutsii-v-rosii/
????? natyazhnye-potolki-samara-8.ru .
?????? ???????? ? ???????? ?????? ??? — ??? ??????????? ???????????? ?? 200 000 ?????? ? ?????, ??????? ??????? ??????????, ??????? ?????????? ??????? ? ??? ?????? ??? ?????????. ?????? ?????????? ??????? ???????????, ?????? ?? ??? ? ??????????-?????????, ?????? ?? ??????????? ????????, ??????????? ? ??????????? ?????????. ??????????? ? ?????? ?????? ???????? ?? https://nabor-curierov.ru/y-food/ — ????? ????? ?????? ???????? ??? ?? ????????? ????, ??????? ?? ??????? ?????????? ? ??????? ????????? ?? ?????? ?????.
?????????? ?????????? ??????????? ?????? — ??? ????????
https://ztube.com.br/@leilanihackbar?page=about
Focused Start Space – Highlights methods to begin projects with clarity and purpose.
claritymapclick.click – Informative hub, encourages users to map out clear action steps for success.
???? ???????? ???????? natyazhnye-potolki-samara-6.ru .
plan ideas effectively – Motivates careful consideration and strategic application of insights.
strategicgrowthhub.click – Motivational content, platform emphasizes smart actions and effective planning.
knowledgeexpansion.shop – Insightful platform, supports users in learning efficiently and growing their skillset.
Action Momentum Hub – Encourages structured steps to sustain momentum effectively.
??????????? «??????????» ????????? ?????? ??????? ?????????????????? ?????????? ? ???????????? ?????? ?? ???????? ?? ?????????? ??????? ???????, ??? ? ??? ???? ? ???????????????? ?? ????????? ? ?????????? ??????. ????? ?????? ????????? ???? ????????? ?? ????? belblokopt.ru ??????????? ??????? ??????????? ???????????? ?????? ????????? ????????? D400-D600 ??? ?????????? ?????, ???????, ??????????? ? ????????? ?????? ?? ???????????? ?????. ???????? ????????????? ????????????????? ???????????? ?? ??????? ???????????????, ?????????? ? ??????????? ?????????? ?????? ?????? ? ???????????? ??????? ??????????????? ? ??????????? ?????????? ????????????.
?????????? ???????? ??????? ?????? natyazhnye-potolki-nizhniy-novgorod-6.ru .
start with intention – Encourages focus-driven actions for effective outcomes.
potolochkin ru ?????? http://natyazhnye-potolki-nizhniy-novgorod-5.ru/ .
Future Options Overview – Breaks down possibilities into an easy-to-follow perspective.
Next Step Journey Hub – Highlights actionable tips for moving into new stages effectively.
stylishhome.shop – Attractive products, navigation is simple and browsing is hassle-free.
???????? ??????? ?????????? ?????? https://natyazhnye-potolki-nizhniy-novgorod-4.ru/ .
modernvaluefront.click – Well-presented selections, platform makes it easy for shoppers to find value and navigate.
keepmoving.shop – Encourages determination and continual progress in all endeavors.
????? ????? ????????????? ???????, ???????? ? ??????????? ?????? — ??? ??????? ?? ????????, ??????? ? ? ???????, ????? ????? ?????? ????????????. ?????????????? ?????????? ???????????????? ?? ???????? ?????????? ?????????? ? ??????????? ?????, ????????? ????, ?????, ???????, ?????? ? ?????? ??????????? ????????. ?????? ????? — ??? ???????????? ?????????, ????????? ? ?????? ????????? ??????? ? ???????????? ???????. ?? ???????? https://www.florion.ru/catalog/buket-belyy ???????????? ????????????? ???????? ????? ?????????? ??? ?????? ??????. ???????????????? ???????? ?? ?????? ???????????, ??? ??? ??????? ???????? ??????? ? ?????????? ???????????? ??????????? ?? ??????????.
apply learned plans – Reinforces consistency after gaining understanding.
?????????? ?????????? ? ??????????? ?????? — ??? ????????
https://fj.sinesation.com/annettbraund96
Next Level Planning – Encourages structured approaches for advancing personal or professional growth.
??????? ?????, ????? ?????? ???????????? ??? ?????? ???????. ?????????? ???????, ???????? ???? ?? ? ????? ??????? ????????????? ? ?????. ??????????, ??? ???????? ??????? ????????????? ?????????? ????????? ????????.
??? ???, ??? ????? ?????, ??????? ??????-???????. ??????? ??????? ????????????? ??? ?????? ????. ????????? ?????????????? — ??? ?????? ????????? ?????????. ???????? ???????, ???? ????? ???????????? ???????? ???????. ??????, ??? ???? ???????? ?? ???????. ?????????? ???? ???????????? ??????????? ????????. ???? ??????? ???????? ? ?????????? ??????? ????????.
forwardmotionhub.click – Inspiring content, guides users to maintain progress and keep moving ahead.
Focused Decisions Hub – Supports making clear, thoughtful choices in daily activities.
gjnjkjr https://natyazhnye-potolki-samara-5.ru/ .
Focus Planning Point – Encourages thoughtful planning around the next area of focus.
Transition Phase Planner – Supports smooth transitions into the next level of achievement.
discover powerful paths – The concept feels strong yet easy to understand, giving an encouraging first impression.
develop abilities guide – Inspires proactive learning and personal growth strategies.
trendhome.shop – Modern and attractive products, site layout makes exploration simple.
?????????? ??????? ?????? ?????? ??? ??????? ??????, ?????????????
https://git.emanuelemiani.it/deangelobridge
chicshop.shop – Stylish products, smooth interface makes exploring items enjoyable.
????????????? ????? ?????? ????????????? ????? ?????? .
Daily Success Steps – Encourages taking small, meaningful actions to create consistent progress.
grow assuredly – Encouraging message with a straightforward path.
Growth Made Simple – Emphasizes straightforward ideas that make growth feel achievable.
Steady Confidence Path – Encourages consistent efforts to grow while strengthening self-trust.
Long-Term Progress Space – Supports establishing habits that sustain momentum effectively.
?????? ??????????? ??????? ?????? — ???????? ??????? ? ?????
https://git.solidityteam.ir/audryolivarez
???? ??
????????????? ?????? ?? ??????????? ? ?????? ? ???????
????????? ?? http://www.natyazhnye-potolki-samara-8.ru/ .
?????????? ?? ???????? ??????? ?????? https://natyazhnye-potolki-nizhniy-novgorod-6.ru/ .
????????? http://www.natyazhnye-potolki-samara-6.ru .
Pathway To Success – Guides in identifying priorities and creating actionable steps.
Growth Discovery Zone – Offers simple concepts that spark interest in ongoing development.
Soft Moon Hub – The calm design keeps browsing enjoyable and inspiring.
?????????? ???????? ???????? — ??? ?????, ??? ?? ??? ??????? ????? ????????? ???????? ??????? ??? ? ?????????? ??????, ????????? ????????? ???????? ???????? ?????????. ??????? ? ?????? ????? ?????? ??? ???????? ????????????? ? ? ???????, ???????? ?????? ????????? ? ??????? ????????. ?????????? ?? ?????, ?????? ?????????? ? ?????? ?????? ?? https://billiardmsk.ru/ — ????? ???? ????????? ??? ????????, ????? ? ????????????? ??????? ????????.
Creative Mind Guide – Encourages thinking innovatively and developing unique approaches.
?????????? ?????????? ?????? ?????? — ?????, ??????, ??? ?????? ????????
https://gitea.jobiglo.com/gavinmcneal18
long term clarity hub – A calm presentation that supports intentional planning.
??????? http://natyazhnye-potolki-nizhniy-novgorod-5.ru/ .
Circular concepts hub – The site combines clarity and insight to promote eco-friendly thinking.
Clarity Focus Hub – Highlights maintaining clear direction to improve productivity and results.
Progress Without Rush – Encourages patient progress built on focused, repeated effort.
?????????? ???????? ?? ???? ??? ????????? ??????? ? ???????. ????????? ???????? ??????????? ? ???????? ???????. ????? ???????? ??????, ????? ??????????. ????????? ???????????? ?????? ??????? ???????. ????? ???????? ?????????: ???????? ???????? ? ???
Build Strategic Focus – Provides tips for maintaining concentration and planning effectively to reach goals.
Taylor Jr project portal – Users can explore work clearly with a professional and appealing design.
Soft Moon Place – The relaxed atmosphere supports an enjoyable browsing experience.
?????????? ?????? ?????? — ??? ?? ?????? ??????
https://heatwave.live/@troyandersen99?page=about
Neighbors for Randy portal – Community-focused content is presented in a clear, accessible format for all users.
Expand Your View Guide – Highlights ways to see situations differently and think creatively.
???????? ????? ? ????????? ???????? ????? ? ????????? .
Intentional Engagement Click – Platform provides a thoughtful experience that inspires deliberate online actions.
??? ???, ???? ????? ???????? ???????? ?? ????, ???? ??????? ???????? ???????? ?????????. ???? ???????, ????????? ??? ????????? ??? zapchasti-dlya-motocikla.biz.ua. ???? ?????????? ????? ?????????????, ???? ???????? ????? ???????????.
??? ???, ??? ????? ?????, ??????? ??????-???????. ????????? ???????? ?? ???? — ??? ????????????? ????????. ???????? ? ??? ???, ??? ???? ???????? ??? ??????????, ? ??? ??????????. ????? ???????? ?????? ???????? ?? ???? ??? ??????. ???????? ??????? ??? ??????? ?????????????. ???? ?? ???????? ?????????, ???? ??????? ?????????. ???????? ??? ??? ??????, ??? ? ??? ??????? ???????.
Luxury Picks – Showcases exclusive products with a focus on quality and refined presentation.
Create Better Paths – Highlights thoughtful choices that guide people toward positive and practical improvements.
potolok http://www.natyazhnye-potolki-nizhniy-novgorod-4.ru .
Identify Your Next Step – Helps pinpoint the actions needed to advance to the next phase.
Next Level Guide – Encourages purposeful steps and building momentum toward success.
Eco learning portal – The site explains ideas effectively, inspiring environmentally conscious decisions.
Game-Lands https://game-lands.ru/ – ??? ???? ? ?????????? ??????? ? ????????????? ??? ???????? ? ??????? ???????. ????? ?? ??????? ?????? ??????, ??????? ????? ? ??????, ?????? ???????????? ?????????, ????????, ????????, ? ??????????? ????? ?? ???????. ???????, ??? ???????? ?????? ??????????, ??? ?????? ? ??????? ???????? ? ? ???? ?????? ? ????? ?????. ???, ????? ???????? ????? ? ???????? ??? ??????????? ??????? ???????.
Idea Compass Hub – Provides guidance to discover and act on strategic growth ideas.
?????? ??????????? ??????? ?????? — 10 ?? 10
https://kolovrat.tv/@roybalsillie40?page=about
Victory Path Planner – Offers tips for navigating routes most likely to produce success.
Otis portfolio portal – Projects are displayed neatly with engaging content for all visitors.
Decision Insights Hub – Inspires critical thinking and careful consideration for successful outcomes.
Support Randy portal – The site encourages neighborhood involvement and provides resources for active participation.
Timber Town Selection – The rustic presentation makes products feel reliable and grounded.
Daily Forward Planner – Supports planning actionable steps that lead to meaningful advancement.
Thoughtful Click Collective – Platform highlights mindful engagement and encourages reflective actions effectively.
?????????? ?? https://www.natyazhnye-potolki-samara-8.ru .
???????? ??????? ?????? https://natyazhnye-potolki-samara-5.ru .
???????? ???????? ??????? ? ??????? ???????? natyazhnye-potolki-nizhniy-novgorod-6.ru .
Growth Explorer – Encourages exploring personal and professional potential effectively.
Practical Learning Hub – Provides easy-to-follow advice for continuous skill refinement.
????????? ?? http://www.natyazhnye-potolki-samara-6.ru .
Innovative Routes – Focuses on finding unique directions that spark ideas and progress.
??????????? ?? ????? — ?????????? ?????????? ??????????? ?????? ?????
https://miduohuyu.com/maziemacrossan
Level Up Compass – Offers strategies for advancing confidently and achieving progress.
Fresh Growth Portal – Inspires discovering new methods for personal and professional development.
Learn And Execute Hub – Offers guidance for transforming learning into immediate results.
Every Mask education portal – Helpful content raises awareness and explains protective measures effectively.
Visit Walk Unchained – Users can explore resources that promote empowerment and connection with others.
Tranquille Eye Cream Guide – Visitors can quickly understand how the product works and its advantages.
Innovative Future Space – Provides actionable tips for exploring ideas and preparing for the future.
Modern Craftsmanship Hub – Elegant handcrafted products are displayed clearly, making navigation enjoyable and easy.
Specialty shop – The items feel handpicked, and the overall display is appealing.
Choice Compass Portal – Helps individuals weigh options and make decisions with clarity.
Knowledge Accelerator – Helps users adopt practical techniques for learning and growth.
?????????? ???????? ?? ???? ??? ????????? ?????? ? ?????? ??????. ????????? 4G ??????????? ? ??????? ???????. ????? ?????????? ???? ??? ???????? ?????????? ?????????. ????????? ?????? ?????? ? ??? ?????? ????????. ????? ??????? ??????? ??? ??????????? ????: https://podklychi.ru/
Deliberate Growth Space – Encourages thoughtful execution paired with steady improvement.
????????? ???????? ??? ???? ???? ???????? ????????????? ????????? ?????. ??????????? ?????? ??????, ??? ???????? ????? ? ????????????. ???????? ???????? ????????? ???? ? ???????? ????. ??????? ??? ???? ????? ? ??????. ????? ?????????? ???????: ??????????? ????????? ?? ???? ? ???????????
???????? ?? ???? ??? ????????? ??? ??????? ??????????????? ? ?????? ????. ????????? 3G 4G ???????? ??????? ????????. ????????? ????????? ????????? ? ???????????????. ?????? ????????? ? ??????????. ?????? ????? ?????????????? ??? ???????????? https://podklychi.ru/
?????????? ?????????? ? ??????????? ?????? — ?????
https://onlain-video.com/@kayleighbunny3?page=about
Keep Moving Forward – Emphasizes continual progress through consistent effort.
Next Step Navigator – Offers guidance to move forward intentionally and achieve measurable results.
Smart Learning Lab – Encourages deliberate learning and thoughtful implementation for tangible results.
Action Driven Growth – Provides insights for keeping consistent forward progress.
Conference hub – Timely updates and detailed schedules are presented in a user-friendly format.
Community events site – News and updates are showcased well, making participation straightforward and engaging.
Focus & Direction Hub – Provides insights to identify priorities and move forward confidently.
a href=”https://saratogapolarexpressride.com/” />Saratoga Holiday Ride – Users can discover ride times, ticket info, and festive activities seamlessly.
Curated Selections Online – Users can explore refined modern items with ease and visual appeal today.
Success Navigator – Guides individuals to make strategic moves for effective results.
???????? ??????? ???????? http://www.natyazhnye-potolki-nizhniy-novgorod-5.ru .
Clean look shop – The minimal design helps the essentials stand out and keeps navigation simple.
?????????? ?????? ??? ??????? ????????
https://qflirt.net/@claudio58e0349
Knowledge Application Hub – Inspires turning insights into effective execution and outcomes.
Action Path Portal – Encourages clear steps toward advancing goals effectively.
Journey To Success Guide – Highlights methods for planning a clear and intentional growth trajectory.
Explore Ember K9 Wish – Heartfelt initiatives for animals are highlighted in a visually appealing manner.
??????? ???? http://www.natyazhnye-potolki-nizhniy-novgorod-6.ru .
Style Trend Hub – Showcases contemporary items and ensures easy and fast shopping.
Maccabees Traders online shop – The site presents items clearly with effortless browsing and organized sections.
«?????????» — ?????? ???????? ?????? ? ?????? ?????????, ???????????? ?????? ?? ???, ??????? ??????????, ????? ? ????????, ??????? ? ?????? ??????? ? ?????????????? ???????? ? ??????? ????????? ??????. ??????? ???????? ??????? ??????? ? ??????????? ???????? ?????????? ?????????? ??? ????? ????? ? ??????. ???????? ????? ? ???????? ?????????? ???? ????? ?? https://evrobuket-nn.ru/ ??? ?? ???????? — ???????? ???????? ??????????, ? ???????? ?? ???????? ?????? ? ???????? ? ???????, ????? ?????? ????? ??????? ??????????.
Worldly Goods Online – The site offers a clean, user-friendly experience for exploring unique global items.
Fitness inspiration hub – The site encourages consistency in workouts and personal growth.
Goal Navigator – Supports planning and taking deliberate, impactful steps.
???????? natyazhnye-potolki-nizhniy-novgorod-4.ru .
?????????? ????????? ??????? ?????? — ????? ????
https://shortee.site/audreypichardo
Classic decor ideas – The layout suggests careful planning, with tasteful products that appear durable.
?????????? ???????????? ?????????? ??? ????????? ?????? ??????????? ????????? ????????? ????????? ????????, ????????? ? ??????? ????????????? ???????? ? ????????? ??????? ????????, ??? ???????? ????? ??? ????????? ??????? ? ?????. ???????? Novatex ?? ????????????? ???????????????? ?? ??????? ?????????????? ?????? ? ??????????, ????????????? ? ?????? ?????????? ?????????????? ? ??????????? outdoor-??????????? — ?? ???????? ? ?????? ?? ??????????? ??????? ????? 7.62, ?????????????? ???????? ?????? ? ????????????? ????????. ?? ??????? https://nova-tex.ru/ ??????????? ??????? ??????????? ???????: ??????????, ????????? ?????????, ???????, ???????, ???????? ????? ? ??????????, ??????????? ??? ??????????? ?????????? ?? ??????? ? ????? ????? ????. ??????? ??????? ???????? ?????????? ????? ?????????? ??????? ?????? ?? ???????????? ?? ????????????, ? ??????????? ?????? ??????? ?????? ??????? ????????????? ?????????? ????????? ???????, ??? ????? ?????????? ????????????? ??????? ? ????????? ? ??????????? ?????? ?? ???????.
?????????? ?????? ???????? http://pechatnakleekmsk.ru/ .
Next Level Success – Encourages focused learning and actionable growth strategies.
Idea Navigator Portal – Encourages developing fresh strategies and applying creative insights effectively.
Forward Path Hub – Helps users navigate clear steps to advance efficiently and consistently.
Next Step Compass – Encourages taking deliberate actions to advance toward meaningful goals.
???? ???????? ???????? https://natyazhnye-potolki-samara-5.ru .
Ethical Click Marketplace – Visitors enjoy a smooth interface while learning about sustainable product choices.
Holy Spirit School EG – The site shares clear details about programs and resources, making it easy for visitors to navigate.
Growth Horizon – Inspires action by pointing out untapped options and future paths.
?????????? ?????????????? ?????? ??? ????????? ??????????
https://therealestatepk.com/author/ramonitamusket/
Learn social issues UK – The site provides informative resources, making important topics easy to understand.
???? ????? ???????????? ? ?????, ????? ???????? ???????? ?? ???? ????. ???????? ??? ??????? ?? ???? ?????? ???????????? ???????. ???? ?????????? ????? ?????????????, ???? ???????? ????? ???????????.
??? ???, ??? ????? ?????, ??????? ??????-???????. ?????????? ?????? ? ??????? ? ????????? ????????????. ????????? ?????????????? — ??? ?????? ????????? ?????????. ??????? ????????? ?????????? ?????? ??????????????. ???????????, ??? ??? ??????? ???? ??? ???????. ?????????? ???? ???????????? ??????????? ????????. ???????? ??? ??? ??????, ??? ? ??? ??????? ???????.
?????????? ???????? ?? ???? ? ??????????? ??? ????? ? ??????. ???????? ???????, ????? ? ?????? ????? ???? ??? ????????. ?????? ????????? ????????? ????????? ??????????? ???????. ????????? ?????? ????? ????????? ?????. ?????? ?? ???? ??? ?? ?????????, ??? ? ??????: https://podklychi.ru/
??????? ????? ????????? ????????, ????????? ? ????????? — ??? ???????? ???????? ??? ????????? ?????? ?????? ??? ???????? ?????????????. ?????????????? ????? ??????? ?????????? ?????????? ? ????????, ?????????? ? ????-??????? ???????? ??? ????? ?????? ???????: ?? ??????? ???????? ?? ?????? ???????? ????????. ??????? ???????? ? ??????, ???????, ?????????, ?????????????? ? ??????? ???????????? ???????, ???????? ??????????? ?????????. ???????????? ?????????? ?? https://www.florion.ru/catalog/buket-rozovyy ????????? ??????? ????? ??? ????? ????? ? ???????? ??????????. ???????? ???????? ????????????? ????????? ?????? ?????????, ? ??????????? ???????? ?? ?????? ???????????? ??????????? ??? ??????? ????????.
??????????? «??????????» https://belblokopt.ru/ ?????????? ??????? ?????????? ???????? ?????????? ? ???????????? ?????? ?? ?????????? ???????? ? ?????????? ??????? ? ?????? ?????? ??. ? ???????????? ???????????? ????????? ??????? ??????????? ?????????????? — ??????????? ???, ????????? ??? ? ??????????? ????????? ????? ????????? D400, D500, D600, ??? ????????? ????????? ??????????? ??????? ??? ????? ???????????? ?????. ????????? ??????????????? ????????? ?????????????????? ? ?????????????????? ??????????, ????????? ? ????????? ? ???????? ??????????.
Next Opportunity Hub – Encourages users to explore fresh ideas and maximize potential.
Coastal Living Market – Creates a soothing atmosphere that supports an easy shopping journey.
Next Step Growth Lab – Provides practical guidance for achieving long-term progress and potential.
Visit Shop Minq – Users can shop stylish products easily thanks to the user-friendly layout.
?????????? ?????????? ??????????? ?????? — ??? ???????? ?? ???????
https://viddex.nl/@thedachampion7?page=about
Focus Navigator – Practical tips for maintaining attention on what truly matters.
Curated Thoughtful Modern – Platform presents modern items in an organized, visually appealing way for smooth exploration.
CryptoTephra online – The site communicates new ideas clearly and maintains visitor interest with engaging content.
?????????? ????? ???????????? ?????? ??????????? ???????? ??????, ???????? ???????????? ??????????? ? ?????? ??? ?? ????? ???????? ???. ?????? Audiomap.ru ?????? ?????? ?????????? ????????? ????????? ?????? — ?? ?????????????? ??????? ?? ?????????? ? ????????????????. ??????? ????????? ?? ????????? ???????? ?????? ????? ???????????? ?? ????: ???????? ??????, ?????, ?????????????? ?????????? ??? ??????????????? ??????????. ???????? ?? https://audiomap.ru/ ? ????????? ?????????? ?????????? ????? ?????? ??? ??????????? ? ?????????? — ?????????? ??????? ???????????? ? ?????? ?????? ??????????????? ? ????????.
Growth Action Compass – Provides guidance for taking meaningful actions that lead to measurable outcomes.
Big Happens Here – The site is lively and fun, showcasing exciting events and experiences to explore.
???????? ??????? ???? ?????? ???????? natyazhnye-potolki-nizhniy-novgorod-5.ru .
Learning & Growth Portal – Encourages applying knowledge to strengthen skills and develop fully.
Mindset Accelerator – Inspires deliberate actions to strengthen growth-oriented thinking.
Soft Spring Boutique – The spring theme feels clean, charming, and nicely balanced.
?????????? ?????????????? ?????? ??? ????????? ??????????
https://www.buyauproperty.com.au/author/janiegerow7196/
Goal Mapper – Focused advice on turning strategy into measurable results.
LIC info portal – Helpful content guides visitors through licensing processes in a clear and accessible way.
Urban Inspired Living – Sleek and trendy platform, site layout is intuitive and products feel modern and appealing.
Douglas and 55 – The site features a clean layout with easy-to-navigate content for visitors.
???????? ?? ????? pechatnakleekmsk.ru .
Explore New Blue Book – Educational and creative, the site inspires users to develop new ideas.
Clarity Path Lab – Provides guidance for mapping out strategic steps and defining a future direction.
a href=”https://growwithintentionalsteps.click/” />small actions matter – Shows how minor efforts can compound into real results.
???????? ????? ???????? ?? ??????? ?? ???? http://www.natyazhnye-potolki-nizhniy-novgorod-4.ru/ .
results roadmap – Provides clarity for taking actions that produce meaningful results.
?????????? ?????????? ? ??????? ?????? — ?????? ? ?????
https://www.soundofrecovery.org/adelamcadams31
Advance Hub – Guides users to improve efficiency and strengthen skills over time.
?????? https://kaimanga.info/ ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
Innovation Scale – Encourages practical approaches to growing ideas and achieving results.
Momentum Builder – Helps individuals stay focused and advance toward objectives efficiently.
Wild Sage finds – The earthy vibe shines through; the products feel balanced and well-presented.
????????? 4G ???????? ?? ???? ???? ????????? ?????????. ???????? ?????????, ???? ????? ????? ????????? ?????????? ????????????. ????????? ????????? ????????? ? ??????. ??????????? ??? ???????? ?????????. ?????? ?? ????????? ??????? ????? ??????? ? ????? – https://podklychi.ru/
LIC Support – The site provides clear guidance and helpful resources for licensing matters.
Refined Global online shop – Well-organized international products make exploring the store effortless.
Curated Market Select – Visitors can explore premium products with clarity and intuitive navigation today.
Unlock Creativity Portal – Provides guidance for discovering new perspectives and unleashing potential.
Idea hub – Browsing is inspiring, with interactive content that encourages creative thought.
??????? ???????? ??? ???????, ?????????? ?????????? ??????? ??????
https://dev.clikviewstorage.com/@elveralieberma?page=about
Davin Chiri Zorve19 ??????????????????????????????????????????????????? https://motionworks.jp/ ???????????????????????????????????
practical growth steps – Supports goal attainment with structured and intentional effort.
Drive Forward Hub – Helps individuals sustain energy and stay on track toward meaningful outcomes.
Growth Navigator – Helps individuals focus on learning and advancing in a structured way.
Learning Action Hub – Helps individuals learn strategically and advance steadily toward their objectives.
Direction Navigator – Helps individuals uncover new opportunities and plan their next steps effectively.
a href=”https://growwithintentionalsteps.click/” />measured growth approach – Supports thoughtful pacing rather than rushed results.
Golden Sage Corner – An elegant structure makes it easy to explore items comfortably.
Madeleine hub – Navigation is straightforward and content is easy to follow for users.
Carefully Curated hub – The platform emphasizes unique items while offering a smooth browsing experience.
Global Craft Hub – The site features curated creative products in a user-friendly and appealing layout.
???????? ????????, ?????? ???????? ?????????? ?????????? ??????, ??????????
https://git.arx-obscura.de/sammiewaterhou
Festive event hub – The platform presents event highlights clearly, making planning for the celebration easy.
outcomes optimization hub – Encourages thoughtful actions to maximize positive results.
Direction Finder – Offers guidance to pinpoint the optimal strategy for long-term success.
Future Growth Compass – Inspires strategic efforts for long-term improvement and personal strength.
Insurance portal – The site presents unique services in a clear and visually appealing way.
Modern Value portal site – Visitors can explore value-driven content with ease and enjoy smooth navigation.
Optimize Forward Hub – Helps individuals refine approaches and enhance progress consistently.
Contemporary Collective Click – Cultural ideas and trends are highlighted clearly, making exploration simple and enjoyable.
?????????? ?????????? ?????? ?????? — ????????? ??????
https://git.miafoxcat.gay/chelseyhatch03
??????? ???????? ?? ????? pechatnakleekmsk.ru .
begin with clarity – Helps establish focus and reduces uncertainty at the start.
clear vision forward – Supports thinking ahead with purpose and actionable steps.
Vision Path Hub – Offers insights for setting clear goals and planning future actions efficiently.
Election engagement portal – Informative content helps citizens understand issues and get involved effectively.
????? ????????? ???????? ???????? ??????????? ???????? ?????? ??? ??????? ? ??????????? ??????????. ????????? ? ????????, ????? ? ????????? ??????????. ???????? ??? ???????, ?????????????, ?????????????? ? ???????? ?????.
???????? ? ?????????? ?????????????? ?? ???????? ????? ????? ?????-????????? ?? ??? ? ????? ? ??????? 24/7 (????? ? ???????) ??? ????????. ??????, ????????????, ??????????, ???????? ???????? ? ????????????. ????????, ???????, ? ?????????????? ?? ?????????????? ? ?????????? ?????.
?????? ??????? ????? ????????? ?? ????? ?? ???? ????????? ??????? ????????, ??????????? ??????, ?????????? ??? ?????? ????????????, ???????? ?????? ? ????????. ????????? ?????? ????????, ???????????? ?????????, ????????? ????? ????????? ? ??????, ??? ???????? ?????.
Forward Steps Lab – Offers insights to explore options and take actionable steps toward long-term goals.
?????? ????????? ??????????? ??????? ?????? — ?????, ????????? ? ????
https://gitea.abra.me/marcelinobonds
Start Smart Hub – Inspires beginning tasks deliberately to maximize efficiency and outcomes.
innovation mindset – Helps readers rethink problems through creative inspiration.
progressive learning path – Encourages structured learning for continuous skill enhancement.
?????????? ?????????? ? ?????????? ?????? — ?????? ? ??????
https://gitea.zerova.com/dexterburger84
????????? ????????????? ?????????? ?????: ?????????? ????????? — ?????? ????????? ???????. ?????????????????? ????? ?????????? ???????????????? ??????? ??? ???, ??? ????? ???????? ? ?????????????. ? ???????????? ???????????? ????????? ??? ????????? ???????????, ????????????? ??? ???????????, ???????? ??????????, ? ????? ???? ? ????? ??????? ??????????????. ??????? ???????????? https://parkmotors.ru/ ??????? ????????? ?????? ?? ????????, ??????? ????????? ????????????? ?????? ????? ??????. ??????? ???????????? ? ?????? ? ??????????? ????????? ??????? ?????? ?????????????? ??????????? ?????????? ??? ?????????????? ? ????????? ???????.
???? ???????????? ??????????? ?? ???????? ????? ????? ?? ????? ? ???????????? ??? ??????????? ?????. ????? ? ????? ?? ??? 24/7, ?????????????? ?????? ??????????, ???????? ????????????, ??????????????????. ???????? ??????????????? ????????? ? ???????????? ?????????? ???????.
????? ?????? ???????????? ?????? ??????????? ???????? ????????, ?????? ????? ? ????????? ?????????. ???????? ???, ?????????, ???????, ??????, ??????? ? ????. ??? ??????? ? ????????. ????????? ???????????? ??????/?? ????????. ?????????? ???????.
Strategic Thinking Hub – Guides users to plan actions effectively with clear strategic insight.
clear path forward – Makes progress feel natural and achievable.
next step strategy hub – Supports users in evaluating options and planning effectively.
impact-focused actions hub – Encourages mapping steps to reach important objectives.
purposeful inspiration hub – Inspires turning insights into tangible results through intention.
Growth Action Lab – Helps users implement practical solutions for continuous development.
?????? ?? ????? — ?????????? ?????????? ?????? ?????? ??? ????????
https://jabrealestategroup.com/author/desireeriegel6/
assured growth guide – Promotes consistent forward motion while boosting self-confidence effectively.
growth route navigator – Guides users to map out and pursue new avenues for success.
??????????? ??????? http://www.pechatnakleekmsk.ru .
intent driven change – Supports growth guided by clear and motivating intent.
progress solutions hub – Encourages discovering actionable opportunities that drive success efficiently.
next move strategist – Supports mapping future actions and exploring possibilities confidently.
idea clarity pathfinder – Encourages structured thinking and turning concepts into practical solutions.
deliberate thinking hub – Supports structured approaches for better decision-making.
action momentum hub – Inspires forward movement with reassuring direction.
future focus navigator – Helps users plan and act strategically to reach desired outcomes clearly.
conceptcreators.click – Resource helping users generate creative solutions and real-world implementations.
results-focused planning guide – Supports executing steps that lead to significant achievements.
?????????? ?????????? ? ??????? ?????? ??????? ?? ?????
https://luxurylinkproperties.ae/agents/corrined664077/
DreamStalker Expert — ?????? ?????????? ????????? ??? ???, ??? ?????????? ?????????? ?????????? ? ????? ????????? ??????????? ???? ? ??????? ???????? ? ???????? ???????? ? ???? REM. ????? ???????? ????????????? tACS ? ??????? ???????????, ???????? ?????????? ?????? ??? ?????????????? ??????????? ???. ???????????, ???????????? ? ????? ???????? ?? https://claps.me/catalog/pribory-dlya-osoznannykh-snov/pribor-dlya-osoznannykh-snovideniy-dreamstalker-expert/ — ? ?????????? ????????? ? ??????? ?????????.
begin clearly – Helps avoid confusion by providing direct guidance for new tasks.
consciousmind.click – Platform inspiring reflective habits and thoughtful lifestyle adjustments.
focused confidence hub – Inspires mindful growth and builds trust in decision-making processes.
pathway insights platform – Inspires planning and taking action on emerging opportunities efficiently.
growth action hub – Inspires taking steps to solve challenges and maintain momentum effectively.
Informed Choices Hub – Inspires users to gather insights and make the most effective decisions.
next step navigator – Inspires exploring upcoming paths and mapping out strategic actions efficiently.
forward thinking paths – Inspires thoughtful exploration of alternative options.
clarity in action – Encourages converting thoughtful ideas into meaningful outcomes today.
discover tomorrow’s paths – Inspires exploration of potential futures with assurance.
strategic foresight guide – Helps map out future opportunities and make decisions with clarity and purpose.
brainstormzone.click – Platform fostering imaginative thinking and turning concepts into action.
????????????? ?????? ? ?????? ?? ??????????? 2026
????? ?????? ?????????? ?????? ??????, ????????? ????????
https://nationalux.com/@clinton20f8151?page=about
????????? ?????????? ??????? ???????????? ????? ? ????????? ????????? ?????? — ?????? ?????? ?????? ????????? ????????? ??????????????? ? ?????????. ???????????????? ?????? ?????????? ??????????? ?????????? ??????: ?? ?????? ??????? ? ?????????? ?? ????????? ?????????? ???? ? ?????????. ???????? ???????? ? ????????????? ??????, ???????, ?????????, ???????? ? ???????, ???????? ?????????? ? ?????? ?????. ??????? ????? ????????? ??????? ??????????? ?? https://www.florion.ru/catalog/cvety-na-svadbu — ????? ???????? ???????? ??? ???????? ?????? ??????? ? ???????. ??????????? ???? ??????? ???????????, ??? ????????? ?????????? ?????? ????????? ????? ??????????? ? ??????????????.
actionable direction guide – Helps users create clear steps to achieve steady results.
structured growth hub – Supports progress without unnecessary distractions or stress.
consciousliving.click – Platform inspiring awareness and thoughtful habits in everyday life.
strategic impact builder – Supports deliberate approaches to achieving measurable success.
strategic execution portal – Inspires turning theoretical knowledge into clear, practical actions today.
progress channel navigator – Helps users identify strategic avenues to enhance outcomes today.
progression hub – Inspires taking steps toward new and effective pathways today.
clarity movement hub – Helps users take intentional steps while maintaining structured progress.
smarter progress guide – Encourages making adjustments to methods for optimized performance today.
momentum starter hub – Helps users plan and execute steps that create continuous momentum.
vision planning system – Motivates converting creative ideas into actionable execution plans.
?????????? ?????? ?????? ?????? ?????? ? ???, ?????????
https://primeluxautos.com/author/carriefizelle8/
growthinsight.click – Hub providing tips and strategies for continuous performance enhancement.
strategic learning guide – Supports aligning approaches for maximum progress.
rise toward better – Encourages ongoing progress through hopeful motivation.
step forward guide – Encourages actionable steps with clear purpose.
ethicalcollection.click – Resource featuring high-quality ethical goods and motivating careful, mindful shopping.
focused success path – Helps maintain direction while implementing strategic steps.
structured growth hub – Supports maintaining consistent momentum while pursuing meaningful outcomes.
intentional growth portal – Encourages thoughtful planning and progress toward meaningful goals.
growth opportunity navigator – Helps users identify and act on new possibilities efficiently.
growth clarity path – Supports intentional progress through clearly outlined actions.
innovative route guide – Encourages users to rethink their strategy and discover clear pathways forward.
?????????? ?????????? ???????????? ?????? — ????????? ????????
https://riserealbali.com/agent/raymontreat067/
intentional opportunity guide – Encourages recognizing purposeful opportunities to move forward efficiently.
Path Forward Hub – Helps users enhance their approach and reach goals with clarity and precision.
progressplanner.click – Tool aimed at organizing steps and maintaining consistent forward momentum.
fresh perspective paths – Helps users identify innovative approaches for steady advancement.
positive growth guide – Encourages developing habits that lead to lasting success.
treasureinsight.click – Hub motivating discovery of concealed assets and unique opportunities.
growth with energy – Encourages maintaining focus while progressing consistently.
fresh ideas corner – Inspires experimentation while keeping the experience engaging.
organized growth hub – Helps users create frameworks that align daily actions with long-term objectives.
opportunity insight portal – Supports discovering overlooked options and maximizing potential strategically.
signal awareness guide – Helps track important indicators for effective action.
ffresh paths forward – Helps reduce uncertainty when looking for new directions.
?????????? ?????????? ???????????? ?????? — ??? ???????????????
https://studioki.re/triciakime4664
main objective guide – Helps users align actions with central strategies and plans today.
forward path portal – Helps users uncover fresh directions and actionable ideas efficiently.
efficient strategy planner – Supports structured thinking and intentional steps for success.
clarityzone.click – Interactive space to organize priorities and sharpen focus.
innovative choice navigator – Supports reviewing strategies and selecting the best possible growth paths today.
growth focus guide – Supports mapping key areas to enhance results efficiently.
moderncollection.click – Resource featuring contemporary products and encouraging seamless browsing.
shared values visa http://www.intercultural.org.au/wp-content/pgs/russian-permanent-residence-permit-investors-complete-guide-2025.html/ .
growth planning navigator – Supports deliberate decision-making for consistent advancement toward goals.
long-term momentum builder – Encourages consistent effort that compounds over time.
????? ?????? ?????????? ?????? ??????, ????????? ????????
https://ueb.li/horacioshoebri
breakpoint planning guide – Helps make intentional choices at pivotal stages.
focused action hub – Supports structured planning and execution for meaningful results.
explore strong directions – Promotes interactive learning with imaginative thinking.
movetorussia com https://ontrack.co.jp/finance/wacc%E5%86%8D%E3%81%B3/ .
movementpath.click – Platform guiding users to build steady energy and drive toward meaningful outcomes.
original strategy hub – Supports developing new approaches with clarity and creativity.
long-term strategy hub – Encourages planning initiatives that sustain growth over time.
progress enhancement guide – Motivates learning and implementing strategies to expand effectively.
step up direction planner – Supports planning actions to reach the next stage of success confidently.
organized goal systems – Reinforces clarity as the foundation of effective planning.
quick growth hub – Helps implement effective strategies for faster achievement.
??????? ???????? ??? ???????, ?????????? ?????????? ??????? ??????
https://whsp.red/ernier8248274
future opportunity hub – Encourages exploring potential pathways with focus and confidence.
elegantmarket.click – Resource presenting curated lifestyle selections with a clean and user-friendly interface.
action impact platform – Supports translating plans into purposeful actions with high effectiveness.
advance learning hub – Helps users gain insights and apply knowledge to progress effectively.
?????????????? https://www.mukakin-blog.com/ ???????????????????????????????????????????????????????????????????????????
stepbystepsuccess.click – Hub supporting users in taking manageable steps toward meaningful outcomes.
goal-directed path – Promotes clarity in decisions and purposeful forward movement.
clear path to growth – Motivates prioritizing key tasks while advancing steadily toward objectives.
strategic action guide – Motivates executing tasks thoughtfully for meaningful outcomes.
goal mapping planner – Encourages clear planning and following steps to reach targets efficiently.
??? ?????: https://malish-nash.ru ????????-??????? ??????? ??? ????? ? ?????????????. ??? ??????????? ??? ??????????? ????? ? ???????? ?????? ???????.
growth with intent – Promotes thoughtful actions that build consistent momentum effectively.
action learning hub – Supports applying insights right away for measurable outcomes.
???????? ????????, ?????? ???????? ?????????? ?????????? ??????, ??????????
https://www.ngiafon.com/video//@grettajyp81499?page=about
aligned growth path – Supports coordinating actions with goals for optimal results.
steady improvement guide – Encourages reliable growth through ongoing focus.
artisanalinsight.click – Resource supporting exploration of handcrafted items and inspiring creative discovery.
forward motion navigator – Provides guidance to move initiatives ahead with clarity and focus.
??????????? ???????? ? ?????????? ????????? ???????????????? ???????? ?????? ?? ????????, ????????, ????????????? ? ??????????? ?????? ? ????? ??? 10-?????? ?????? ??????. ?? ????? https://yuridicheskaya-kompaniya-krasnodar.ru/ ???????? ?????????? ????????? ???????????? ? ???????? ?????????? ? ?????????? ????. ???????? ???????? ????? ?????????? ? ????? ???? ???????, ????????? ?? ????????? ?????????? ? ??????? ???????? ???????? ? ???????????? ???????????????? ?????????????? ??????????? ??????? ????????? ?????????.
opportunity explorer – Guides users to identify novel pathways for progress effectively.
futuregrowth.click – Resource assisting in identifying pathways for sustainable improvement and success.
??????????????????????https://ropc.jp/ ?????????????????????????????????????????????????????????????????????????????????????????????????
growth clarity platform – Supports attentive and organized approaches to reach objectives effectively.
strategic success path – Supports taking deliberate steps along well-defined routes for better results.
shared values visa http://ai.thestempedia.com/news/remote-work-from-russia-guide-for-digital-workers-shared-values-visa.html/ .
new ways forward – Sparks interest while keeping ideas easy to absorb.
strategic start hub – Encourages focused beginnings to achieve meaningful outcomes.
growth paths navigator – Motivates finding hidden avenues that lead to meaningful progress.
?????????? ?????????? ?????? ?????? — ????? ?????? ????
https://compartomisrecetas.com/@kennithgamez5?page=about
decisive growth path – Inspires deliberate actions and confident movements toward success.
????? ???????????? ???????? ?? ???????? ????? ?????????? ????????? — ?????? ???????? ????????????? ???? ??-???????? ???????????? DVD-??????? ??????? ????????. ?????????????????? ????????-??????? ?????? ???????????? ????????? ??????????, ??????????, ???????? ? ????????? ???????? ?? ?????? ? ???????????????? ?????????. ????? ?? ??????? ??? ????????? ????????, ??? ? ?????? ??????? ?????????????. ??????? ????????? ?? https://serialexpress.ru/ ????????? ?????? ????? ?????? ??????, ? ???????? ?????? ??? ???? ???????? ?? ???? ??????. ?????? DVD ??????????? ?????????? ???????? ??????????? ??? ??????????? ?? ???????? ????????? — ????????? ??????? ??? ????????? ?????????.
Forward Path Hub – Encourages practical first steps toward enhancing skills and personal growth.
strategy optimization guide – Encourages refining plans to achieve better outcomes consistently.
start smart portal – Motivates thoughtful action and strategic planning for consistent progress.
moderncollection.click – Resource highlighting fashionable global items and encouraging effortless exploration.
actioninsight.click – Platform helping users develop strategies and take purposeful steps toward success.
clear path launch – Encourages users to initiate plans while maintaining focus on key outcomes.
build better outcomes – Promotes smart actions that lead to meaningful change.
planning for progress – Motivates clear planning and step-by-step implementation for better results today.
goal planning portal – Inspires focusing on strategic actions to achieve objectives efficiently.
?????????? ?????????? ?????? ?????? — ????????? ??????
https://freshtube.net/@maddison64d917?page=about
???????? ? ??????? https://www.stomatologiya-v-bare.com ??????? ??????? ? ???????, ?????????????? ????? ? ????? ????, ?????? ?????? ?????. ?????????????? ??????, ??????????? ??????????, ????????????. ?????????? ?? ???????????? ? ???????? ???? ???????.
long-term strategy hub – Encourages thoughtful planning and deliberate steps for growth.
movetorussia com http://www.absolutecreativemarketing.co.uk/pages/best-5-russian-immigration-services-for-uk-citizens-2026.html .
progress-oriented approach – Guides users toward consistent execution and goal attainment.
focused strategy platform – Motivates adopting methods to ensure reliable and structured growth today.
purpose-driven start guide – Encourages launching tasks with intentional direction and focus.
???? ???????????? ??????????????? ?????. ????????? ????????? ?????????? ??????? ? 1976 ?. ????????? ? ?. ??????? ????????????? ???????. ???????? ???????? ????????????? ???????? ??????????? ????????, ???????? ?????????????? ????, ???????????, ????, ????????, ???????? ??????? ??????, ????????????? ???????????, ?????????, ???????? ??????, ? ????? ???????????????? ?????????. ????? ?????????? “?????????? ??????? ? ?????????? ?. ????????”, ??????? ???????? 154 ??????? ? ???????? ?? ??????? ????, ?????????? “??????????? ??????????? ?????? ?. ????????” ? ??????? ?????? ????? «???????? ??????». ???????? ?????????????? ????????. ?????? 5 ???????????? ????????. ???? ????? ??????? ??????????. ???? ???????????? ??????????????? ?????. ???? ????????????? ????? «?????????? ? ?????????» ???? ????? ????????? ??????. ???? ??????????? ????? ?????????. ??????? ?????????????? ??????? ???????? “Artex Awards”. ??????? ???????? “?????? ????????”. ?????????? ????????????? ???????????????? ???????????? ???????? Poetfest’24. ?????????? ???????? «?????? ?????» ? ????????? «????? ????????». ????????? ??????? «225 ??? ?. ?. ???????», ?????? «??????? ???? ??????? ??????????», ??????? «?? ?????????? ??????? ???????????? ????????» ??. ??????? ??????? ?????, ??????? ????? ?. ?. ???????? «?? ??????????, ??????????? ? ??????????????» ?? ????????????? ???????? ??????? ???????????, ??????? ????? ??????? ???????????? ????????? «??????? ?????? ????», ??????? «?? ??????? ? ???????? ? ?????????», ???????? ???????? ??????? ????????? ?????????????? ???????? «????? ??????? ??????», ???????? ???????? ??????? “?? ????????? ? ??????? ? ?????????????? ???????? ??????”, ??????? ?. ?. ?????? «?? ?????? ???????», ??????? «130 ??? ?. ?. ???????».
deliberate growth navigator – Inspires users to act with clear focus and purposeful direction.
???????? ? ????? ???????????? ? ??????? ?? ??? ??????????? ?? ?????, ?????? ?????????, ????? ????????? ?????????, ?????? ????????, ?????? ??????????????? ? ????, ????????? ????????????. ??????? ?????? ?? ?????? ? ???????. ??????? ????, ????????, ??? ?????? ?????.
action implementation platform – Encourages taking immediate steps to achieve long-term objectives efficiently.
urbantrendstore.click – Trendy city-focused items are highlighted, helping users embrace modern living.
growthinsights.click – Resource providing practical guidance for boosting performance and realizing outcomes.
innovation pathway portal – Inspires taking strategic action toward untapped opportunities.
?????? ??????????? ??????? ?????? ???? ?????? ??????
https://git.infortek.tech/zzqdonald30016
opportunity pathfinder – Supports finding and acting on development possibilities efficiently.
learning with purpose – Encourages using acquired knowledge to take intentional, forward-moving steps.
?????????? ?????????? ?? ??????????? ????? ??????? — ??? ?? ?????? ?????????, ? ?????? ????????? ?????? ?????????? ? ????? ????. ? ????????-???????? «???????» ?? ?????? https://www.florion.ru/catalog/novogodnie-kompozicii-iz-nobilisa ???????????? ????? ??????????? ?? ????????, ??????? ????? ?? ????????? ? ????????? ?????????? ??????? ??????. ???????? ??????????? ?????? ?????? — ?? ????????? ?????, ????? ? ?????? ?? ???????????? ???????? — ???, ????? ?????????? ????????? ????????? ? ???????? ? ????? ????? ??????? ???????????? ?????? ? ????????, ????? ??? ?? ?????????? ?????.
advancement navigator – Encourages gradual skill building and practical application.
???????? ? ??????? https://www.stomatologiya-v-bare.com ??????? ??????? ? ???????, ?????????????? ????? ? ????? ????, ?????? ?????? ?????. ?????????????? ??????, ??????????? ??????????, ????????????. ?????????? ?? ???????????? ? ???????? ???? ???????.
strategic idea explorer – Motivates exploring alternative plans and innovative solutions clearly.
focused execution path – Promotes consistent action aligned with clear goals.
shared values visa https://www.prathamonline.com/js/pgs/?russian-permanent-residence-permit-guide-investment-and-citizenship-path.html .
????????????? ???????????? ????????? https://www.sportprof.su/ ?? ???????????? ????? ? ??????? ?????????. ?????-???? ???????? ??????, ??????????? ?????, ??????????. ?????? ??????? ?????????????? ??????? ????????? ? ???????? ??? ????????? ?????????? ?????????? ?????. ?????????? ?????? ??????????????????? ?????? ?????, ???????????-?????????????? ????, ????? ??????, ?????? ??? ?????, ??? ??????, ??????? ????, ??????? ???? ??? ?????, ? ????? ??????? ?????? ?????? ??????????.
???????????? ? ?????? https://albakaluga.ru ????????? — ??????????? ? ?????????????? ????? ? ????????? ????????. ??????, ??????? ???????? ? ??????????? ?????? ?? ??????????????? ????? ???????.
opportunityexplorer.click – Hub designed to guide exploration of innovative solutions and growth paths.
strategic action navigator – Encourages taking intentional and well-planned steps toward success.
curatedmarketplace.click – Hub highlighting top-quality products while offering smooth, easy navigation.
?????????? ?????????? ?????? — ?????? ????????????? ??????
https://git.u2.nu/graciela653337
phase insight hub – Supports understanding the next stage and setting practical steps clearly.
??????????? — ???????? ????????? ????????? ??? ??????????? ?-170, ?-130, ?-10 ? ????????????? ??-98, ????? ??????? ??????? ????????? ?????? ????? ???????????. ???????? ???????????????? ?? ??????? ??? ??????? ???????????, ?????????? ??????????? ???????????? ??????, ?????, ????????? ????? ? ?????? ????????????????? ???????. ???? ??????????? ? ???????? ???????? ?? https://trak74.ru/ — ????? ????? ?????? ???????? ???????, ??????????? ????? ? ???????? ?????? ??????? ??? ?????? ???????.
The best reads here: https://etarp.com/cart/view.php?returnURL=https://th.wikipedia.org/wiki/%E0%B8%9B%E0%B8%A3%E0%B8%B4%E0%B8%A8%E0%B8%99%E0%B8%B2
Looking for roulettuno casino avis? Visitez le site officiel du Roulettino Casino casinoroulettinofr.com en France et vous pourrez obtenir des bonus intéressants lors de l’inscription et de l’activité, ainsi que des tours gratuits gratuits. Découvrez-en plus sur notre établissement et notre ludothèque – un large éventail qui comblera les attentes de chaque joueur. Transactions financières simplifiées pour les dépôts et retraits, plus une appli mobile ergonomique à disposition.
structured direction guide – Guides users to align priorities and act with purpose.
????? ?? ??????????? ??? ???????? ? ?????? ? ???????
????? ?????? ????? https://www.unitalm.ru “??????-?” ???????? ???????? ?? ?????? ????? ????? ??? ?? 350-?? ??????????, ? ??? ????? ?? ??????????????????? ? ???????? ????????????. ? ????? ????????? ?????? ??????????????????? ? ????????? ???????????? ? ??????????? ?????? ?????.
clarity-driven learning – Helps users transform their approach using informed insights efficiently.
progress advancement platform – Helps users stay motivated while making steady improvements today.
???? ????????????? ????? «?????????? ? ?????????» ????????? ????????? ?????????? ??????? ? 1976 ?. ????????? ? ?. ??????? ????????????? ???????. ???????? ???????? ????????????? ???????? ??????????? ????????, ???????? ?????????????? ????, ???????????, ????, ????????, ???????? ??????? ??????, ????????????? ???????????, ?????????, ???????? ??????, ? ????? ???????????????? ?????????. ????? ?????????? “?????????? ??????? ? ?????????? ?. ????????”, ??????? ???????? 154 ??????? ? ???????? ?? ??????? ????, ?????????? “??????????? ??????????? ?????? ?. ????????” ? ??????? ?????? ????? «???????? ??????». ???????? ?????????????? ????????. ?????? 5 ???????????? ????????. ???? ????? ??????? ??????????. ???? ???????????? ??????????????? ?????. ???? ????????????? ????? «?????????? ? ?????????» ???? ????? ????????? ??????. ???? ??????????? ????? ?????????. ??????? ?????????????? ??????? ???????? “Artex Awards”. ??????? ???????? “?????? ????????”. ?????????? ????????????? ???????????????? ???????????? ???????? Poetfest’24. ?????????? ???????? «?????? ?????» ? ????????? «????? ????????». ????????? ??????? «225 ??? ?. ?. ???????», ?????? «??????? ???? ??????? ??????????», ??????? «?? ?????????? ??????? ???????????? ????????» ??. ??????? ??????? ?????, ??????? ????? ?. ?. ???????? «?? ??????????, ??????????? ? ??????????????» ?? ????????????? ???????? ??????? ???????????, ??????? ????? ??????? ???????????? ????????? «??????? ?????? ????», ??????? «?? ??????? ? ???????? ? ?????????», ???????? ???????? ??????? ????????? ?????????????? ???????? «????? ??????? ??????», ???????? ???????? ??????? “?? ????????? ? ??????? ? ?????????????? ???????? ??????”, ??????? ?. ?. ?????? «?? ?????? ???????», ??????? «130 ??? ?. ?. ???????».
????? ????????????????????? ? ????????? ???? ????? ?????: ????????? ????????????????????? ? ??????????? ?????.
unlock growth potential – Helps users find opportunities that drive significant progress efficiently.
daily focus roadmap – Motivates structured action toward meaningful outcomes.
?????? ?? ????? ?????? — ??? ???????????? ???????, ??????? ?????????? ????? ? ????????? ???-??????. ? ????????-???????? «???????» ?? ???????? https://www.florion.ru/catalog/loshadi-iz-cvetov ?? ??????? ?????????????? ??????????, ????????? ??????? ?? ?????? ??????? ? ??????. ????? ?????????? ???????? ????? ?? ??????? ??????????, ??????? ? ???????????? ????????????: ??? ?????????? «???-??????», ??????? ????????? ? ????????? ? ????? ????????? ?????????? ??????? ???, ??????????? ?????? ? ???? ????????.
???????????????? ????????? ?????????? ?????????? ????? ??????????? ? ?????????????? ???????, ???????? ?????? ????????? ? ??????????? ?????? ???????. ?????????????? ?????? ???????????????? ?? ????????????? ????????????? ??????????, ???????????, ????????, ???????? ? ??????? ???????? ?????? ???????. ??????? ????????? ????????????? ????????? ?????????? ? ?????? ???????? ???????, ?????????? ????? ???????? ??? ????????? ?????????. ????????? ??????????? ???????? ????? ??????? ?? https://www.florion.ru/catalog/oformlenie-meropriyatij-cvetami — ????? ???????????? ???????? ??? ???????? ??????? ????????. ?? ?????????? ?????????? ?? ?????????? ??????????? — ?????? ??????? ????????? ? ????????? ? ??????? ? ????????? ???????? ????????.
?????????? ??????? ?????? ?????? ????????, ??????? ???????
https://gitea.opengl24.de/anjawolak89325
artisancollective.click – Hub showcasing global craftwork and motivating discovery of exceptional artistry.
https://1absolut.ru/
????? ????????? ???????? ???????? ??????????? ??? ???????? ?????????? ????????? ??????? ? ???????. ????????? ? ????????, ?????????? ???????, ???????? ???????? ???? ??? ?????????. ?????? ???????? ? ???? ?????, ??????? ???????? ? ????????.
intentional success path – Helps users align actions with long-term goals for effective growth.
????? ?????????? ??????? ????????? ? ??? ?????? ??????? ????? ?? ?????-?????????? ? ???????. ????????? ???????? ???????? ????, ?????????, ????????. ????????? ????? ??? ? ???????, ?????? ? ????????/???????. ?????????? ????, ??? ???????????.
?????????? ?????????? ? ??????? ?????? — ??? ?? ??????
https://houseplusplus.titancorpvn.com/author/roxienason722/
Moving to Russia https://actuabd.com/cookies/articles/?life_in_russia_a_guide_for_new_expats.html .
Growth Focus Portal – Provides guidance for structured actions that maximize consistent improvement.
Russian Golden Visa http://www.www.lagodigarda.com/booking/pages/shared_values_visa_programs_a_new_path_for_global_citizens_2025_mobility_guide.html .
?????????? ?????????? ? ?????????? ?????? — ?????? ? ??????
https://library.ithyxy.com/blancaconstant
?????? ?????? ?? ?????: ???? ????? ???? Girard-Perregaux ?????? — ?????? ????? ?? ????
????????????? ?????? ? ?????? ?? ??????????? 2026
?????????? ??????? ?????? — ?????, ??????, ????????
https://mupf.me/marilynnheywar
????? ?????????? ????? ?????????? ? ??? ?????? ??????? ????? ?? ?????-?????????? ? ???????. ????????? ???????? ???????? ????, ?????????, ????????. ????????? ????? ??? ? ???????, ?????? ? ????????/???????. ?????????? ????, ??? ???????????.
????? ????????? ???????? ???????? ??????????? ???? ??? ???????? ?????????? ????????? ??????? ? ???????. ????????? ? ????????, ?????????? ???????, ???????? ???????? ???? ??? ?????????. ?????? ???????? ? ???? ?????, ??????? ???????? ? ????????.
?????????? ?????????? ? ?????????? ?????? — ?????? ? ??????
https://platform.giftedsoulsent.com/dorrisderose37
Balanced digital interface – A well-structured experience that feels smooth and responsive
Action learning platform – Helps take direct steps to enhance competence and efficiency
Strategic transformation guide – Helps users adjust plans and take decisive steps forward
movetorussia com http://www.copychief.com/art/how_to_relocate_to_russia_moving_guide.html .
Forward-thinking hub – Encourages taking fresh steps toward innovative solutions and opportunities
Creative thought launcher – Supports developing unique ideas and applying solutions effectively today
?????????? ?????????? ?????? ?????? — ??????? ?????? ??????
https://realpondy.com/author/josettepolk21/
purposedrivengrowth.click – Thoughtful advice supports careful steps toward measurable outcomes
????? ??????? ????? ?????: ???? ??????? ???????? ??????? — ?????? ? ??????????? ??????
growthstepplanner.click – Practical guidance promotes taking intentional steps toward advancement
a href=”https://explorefreshopportunitypaths.click/” />freshopportunityplanner.click – Practical tips help explore and act on new opportunities efficiently
Creative progress guide – Supports discovering new paths for effective and forward-focused actions
growstrategicallytoday.click – Structured tips support deliberate actions to achieve consistent growth effectively
Responsible style guide – Makes ethical choices feel natural and appealing
«???? ???» — ?????? ???????? ???????? ???? ?? ??? ? ? ???? ? ????????? ? ?????????, ??? ?????? ?????????? ?????? 19 ? 5 ??????, ?????? ? ????????????? ?????? ????? ???? ??? ????????? ??????????. ???????? ?????????? ??????????? ????????, ??????????????? ????????? ? ??????? ??????????? — ?? ??????????? ???? ?? ????? ? ???????????. ???????? ????? ? ?????? ?????????? ???? ????? ?? https://voda-s-gor.ru/ — ?????? ???????? ??????, ?????????? ? ? ???????? ?? ???????? ???????.
pathwaytogoals.click – Insightful advice supports planning next steps and achieving meaningful progress
Forward Focus Hub – Encourages achieving goals decisively while building personal confidence.
Smart creativity navigator – Helps generate inventive ideas and actionable plans efficiently
?????????? ?????????? ? ??????????? ?????? ?????? ?? ???
https://sophron.ru/horacebaskin8
rethinkandgrow.click – Practical guidance helps users shift their mindset and implement transformative actions today
?????? — ?????? ? ?????????? ??????? ????????, ?????????? ? ???????????? ?????????, ? ??????? ????????? ???????? ?????? ????. ?????????????? ?????? ?????????? ????????????? ????????? ? ?????????? ????????, ??????? ????????, ??????????? ????????????????? ? ?????????? ???????? ?? ?????? ????????. ?? ???????? ?????????? ?? ??????????? ??????????????? ???????? — ?????? ?????????? ?? https://ruria.ru/ ????????? ????? ????? ????? ??????. ???????????????? ?????? ?????????, ??????????? ????? ? ???????????? ??????? ?????? ?????? ??????????? ??? ???, ??? ????? ????? ???????? ???????????? ?????? ? ????????? ???????????? ????? ??????.
alignedactionpaths.click – Practical guidance supports coordinating steps and objectives for effective advancement
growthconfidencehub.click – Practical content encourages progressing with certainty and purpose
intentionalfocusplan.click – Practical strategies foster deliberate and well-directed progress
Direction clarity guide – Encourages understanding options and taking confident actions
Path clarity hub – Encourages structured refinement of methods for consistent growth
Visionary growth space – Inspires strategic exploration of innovative directions
strategyprogressnavigator.click – Practical tips support acting with strategy to generate meaningful outcomes
a href=”https://explorefreshopportunitypaths.click/” />freshgrowthpaths.click – Focused tips encourage discovering innovative directions for meaningful progress
?????????? ????????????? ?????? — ?????? ????????
https://tovegans.tube/@markalcala072?page=about
stepforwardnavigator.click – Motivating guidance highlights taking well-defined steps to continue progressing
Growth navigation platform – Helps structure decisions and choose paths that lead to steady advancement
growthmindsetstrategies.click – Motivating guidance supports transforming thought patterns into practical outcomes efficiently
effectivegrowthalignment.click – Motivating content helps users align plans with outcomes for consistent advancement
Goal to execution flow – Creates a smooth path from vision to measurable action
????? ??????? ???????? ???????? ??????? ????????????? ???????? kix-med.ru ? ??????????? ?????????? ??????????? ??????????? ?????? ?? ??????????, ???????????, ???????? ? ??????????? ? ??????????? ????????? ??????????? ? ???????????? ?????????? ???????. ??????? ????? ???????????? ?????? ????????? ??????? ????????????? ?????????????, ???-??????????? ? ?????? ???????????? ? ??????? ??????????. ???????????? ?????? ? ?????? ???????????, ???????? ?????????? ? ??????? ???????? ???????? ??????????? ???????? ??????? ???? ??????? ??????????? ???????.
???? Xrumer ?? ????? ???? ???????? Xrumer ????????: “???????????” ???? ??? Xrumer, ???????????????? ? Telegram. ??? ?????, ??? ??? ????? ?? ????? ?????????????, ??? ???? ????????????? ??????? ? ??????????.
Visit https://krootez.com/ and you can buy Instagram followers, likes, and views at the best price! We offer exclusive and fast services. Explore our offers and all the benefits of working with us! Simply choose a service and instantly get followers, likes, views, and comments.
organizedprogress.click – Insightful tips encourage structured planning for consistent advancement
Progress learning hub – Supports applying new methods to expand growth and achieve goals effectively
quicklevelup.click – Insightful guidance encourages taking decisive action toward higher objectives
????? ????????? ???????? ???????? ??????????? ?????? ??? ???????? ?????????? ????????? ??????? ? ???????. ????????? ? ????????, ?????????? ???????, ???????? ???????? ???? ??? ?????????. ?????? ???????? ? ???? ?????, ??????? ???????? ? ????????.
????? ?????????? ??????? ????????? ?????? ? ?????? ??????? ????? ?? ?????-?????????? ? ???????. ????????? ???????? ???????? ????, ?????????, ????????. ????????? ????? ??? ? ???????, ?????? ? ????????/???????. ?????????? ????, ??? ???????????.
Undiscovered growth hub – Encourages actionable exploration of overlooked paths to success
?????????? ?????????? ?????? ????????
https://vidspace.store/@millardsneddon?page=about
intentionalmindhub.click – Motivating guidance encourages thoughtful planning and purposeful actions for results
??????? ????? ??????? ?????? ?? ????? ? ???????? – ??? ????????? ???????? ??????, ????????? ??????? ? ??????????? ?????????.
progresscontinuitymap.click – Practical guidance emphasizes steady steps and maintaining long-term movement
learnforwardhub.click – Structured advice promotes learning new skills and executing strategies effectively
Growth action planner – Encourages leveraging strategies to reach goals efficiently and effectively
Strategic growth hub – Helps identify and act on opportunities for continuous development
thoughtfulbegin.click – Forward-looking platform encourages initiating actions with direction and deliberate focus
smartplanninghub.click – Motivating platform highlights effective strategies and thoughtful planning for growth
futurefocusplanner.click – Insightful tips guide setting priorities and long-term targets effectively
?????? ??????: ??? ??????? ??????? ??????? — ???????? ?????? ? ?????? ??????????
Growth roadmap guide – Supports planning frameworks to guide clear and deliberate growth
?????????? ??????? ?????? ?????? ?? ??????
https://www.hyzq123.com/@elizbethduffy7?page=about
??? ???????????? ????? ?????? ? 1win
Focused movement ideas – Supports clarity while moving steadily ahead
Intentional progress guide – Helps maintain focus and act with purpose every step of the way
growthnavigatorhub.click – Practical advice highlights fresh opportunities and ways to act on them immediately
https://frontiesta.com/ ??????????????????????????????????????????????????????????????????????????????????????????
resultsfocusplanner.click – Practical content emphasizes actionable steps for measurable strategic growth
longtermprogresshub.click – Thoughtful strategies keep momentum consistent for sustainable success
Sustainable growth platform – Inspires applying methods that maintain progress consistently over time
freshgrowthpath.click – Motivating advice emphasizes new approaches and structured strategic thinking for success
freshanglesmap.click – Focused guidance emphasizes identifying and acting on fresh insights effectively
Result-driven planning – Encourages making actionable progress without delays
visionstrategyhub.click – Practical platform highlights steps that align with meaningful, vision-driven objectives
strategicpathplanner.click – Structured guidance ensures consistent results by aligning vision with actions
????? ??????? ?????????????? ??????? ??? ????????? ???????? ???????? https://www.akb24v.ru/ ? ?? ??????? ????????? ??????? ??????? ?? ???? ??? ?????? ??????? ??? ???. ???????? ????? ??????? ? ??? ? ??????? ? ?? ????? — ???????????? ??? ??????? ???????? ??????????????, ? ????? ??????? Still, Jungheinrich, Yale, Hangcha, Daewoo, Toyota ? ?????? ??????. ????????? ?? ?????.
?????????? ?????????? ??????????? ?????? ?????? ? ??? ????????
https://yeteneksensin.com/@tabathaclibbor?page=about
Momentum strategy guide – Encourages planning deliberate steps to achieve steady progress
?????????
Forward growth guide – Provides structured approaches to drive measurable results
focusedplanhub.click – Practical content helps users plan effectively and take deliberate actions today
Clear strategy launchpad – Inspires beginning work with intention, focus, and structured guidance today
forwardfocusplanner.click – Motivating tips encourage identifying essential focus areas and planning next steps
growthfocusnavigator.click – Practical tips help users align their actions with strategic priorities effectively
?????? ?????????? ????? seo ?????????? ???? ???????? ?????????? ???????????????? ?????? ?? SEO???????????? (Search Engine Optimization) — ?? ??????? ??????? ?????? ? ????3 ????????? ?????? Google ? ?????? ????? ?? ?????. ?????????????? ???????? ?? ?????????? ??????: ??? ?????????????? ??????????? ? ??????????? ????????, ??? ??????????? ???????? ?????????????? ? ??????????? ? ?????????? ??????????.
Simple progress cues – Keeps direction clear without added complexity
Clarity Forward Hub – Guides users to organize ideas and take focused steps toward achieving their goals.
focusyourgrowth.click – Practical tips highlight where to direct energy for maximum impact
forwardthinkinghub.click – Practical advice promotes exploring and applying innovative growth methods
???????????? ???????? ???? ? ????? ??? ???? — ??? ?? ???????, ? ????????????? ??? ???????? ? ????????. ?????? ???????? ?????????? ?????? ???? ? ??????? 19-???????? ??????? ??? ????????????? ? ???????? — ?????????? ??????? ??? ????? ? ???????????. ? ???????????? ???????????? ??????????? ????? ?? ???????????? ?????? ????????: «????????», «?????», «???????????», «?????» ? ??????. ???????? ???? ? ??????????? ????????? ????? ?? https://voda-s-gor.ru/pitevaya-voda-19l/ — ?????? ???????? ? ????????? ? ?????????. ?????????? ????????, ????????? ???? ? ??????????? ?????? ??????? ?????? ?????? ? ???????? ???????? ???? ??????? ? ??????? ??? ??????? ???????.
progressdirectionguide.click – Insightful platform highlights actionable pathways for achieving meaningful objectives
Focused action guide – Provides clear methods for turning strategy into results
?????????? ?????????? ??????? ?????? ?????? ? ??? ??????
https://estboproperties.com/author/melodythow9072/
????? ?????????? ??????? ????? ????????? ???? ??????? ????? ?? ?????-?????????? ? ???????. ????????? ???????? ???????? ????, ?????????, ????????. ????????? ????? ??? ? ???????, ?????? ? ????????/???????. ?????????? ????, ??? ???????????.
Growth clarity platform – Helps users take intentional steps toward focused and measurable progress
stepforwardgrowth.click – Clear guidance helps take measured steps to reach long-term goals
????? ????? ???????? ?????
??????? ????? “??????” https://sakura-pitomnik.ru/ ???????????????? ?? ??????? ???????????? ? ???????? ???????? ?? ??????? ??????????? ? ?????????? ?????????? ? ????????? ?? ?????-?????????? ? ????????????? ???????. ??????? ???????? ???????? ? ?????????? ??????, ???????????? ??????????, ??????? ????????, ??????????? ?????, ??????, ????????? ????? ? ?????????? ?????? ??? ?????????? ??????????????? ???????? ???????. ??????????? ????????? ????????? ???????????????? ?????? ?? ??????????????? ???????? ? ???????????? ????????????????? ???? ?? ??????????.
hiddenopportunityhub.click – Insightful content helps identify overlooked chances and take actionable steps today
Momentum mapping guide – Helps pinpoint the right time and place to advance efficiently
Strategic action platform – Inspires taking intentional steps to build and sustain momentum effectively
untappedstrengthnavigator.click – Motivating content highlights uncovering personal or organizational strengths for better outcomes
direction building resource – The insights feel relevant and simple to act on.
consistentprogresspath.click – Guidance emphasizes taking deliberate steps to ensure continuous advancement
?????????? ?????????? ??????????? ?????? ?????? ? ??? ????????
https://git.dacremont.xyz/nathanielhuey
momentumstrategyguide.click – Motivating content highlights advancing with clear focus and forward-looking strategies
Forward momentum guide – Supports taking deliberate steps along the most effective path for growth
learn and execute – Tips are practical and make starting right away easy.
explorejadenurrea.click – Thoughtful content delivers reliable advice and interesting ideas for readers
unlockgrowthroutes.click – Focused advice encourages finding actionable ways to progress quickly
Positive growth hub – Offers guidance to build systems that promote steady and consistent progress
opportunity discovery roadmap – Insights make navigating potential opportunities simpler.
rapidstrategyplanner.click – Structured tips guide fast evaluation and planning for effective outcomes
Goal oriented thinking – Helps identify practical steps for achieving results
forward momentum roadmap – Helps users stay motivated and productive over time.
strategicactionmap.click – Focused content helps translate planning into measurable, consistent outcomes
Improvement execution guide – Helps users implement practical steps for immediate gains
growth path resource – The information feels relevant and easy to implement.
Actionable growth finder – Supports recognizing paths that deliver measurable results and forward motion
visionstepplanner.click – Practical content helps users clarify their goals and map a clear strategy for success
?????????? ???? ?????? ?? ??????? ????, ????????? ? ???????
https://git.repo.in.net/terrellumbagai
Impactful journey hub – Supports exploring paths that lead to meaningful progress and growth
learnandexecuteeffectively.click – Practical guidance helps users learn and implement strategies efficiently today
progress made simple – The guidance is clear and encourages immediate, practical steps.
turningpointmap.click – Focused tips highlight actionable moments and guide progress strategically
explore potential paths – Content encourages organized and focused exploration.
strategicimpactmap.click – Focused tips help create actionable plans that drive measurable results
Goal-driven growth platform – Supports deliberate steps to achieve concrete outcomes
focusedgrowthsteps.click – Strategic tips foster steady advancement by highlighting crucial priorities
growth focus corner – The ideas are practical and feel easy to adopt.
?????????? ?????? ?????? ?????? ?????? ? ???, ?????????
https://gitea.codedbycaleb.com/retamauro26923
Forward movement platform – Inspires taking clear, organized steps and monitoring progress continuously
impactstepshub.click – Practical guidance helps turn plans into actions that generate real results today
Strategic clarity space – Encourages precise thinking and actionable outcomes
sustained progress ideas – Encourages focused actions that build long-term results.
?? ????? ????? ?? ?????
Rapid execution guide – Supports turning knowledge into impactful growth steps quickly
???? ? ??? https://auto.ae/ ??? ????: ??????? ????? ? ?/? ???????????, ??????????? ????? ????????, ??????????? ? ?????????. ?????? ?? ????? ? ?????????, ??????? ???????. VIP ???????? ????? — ?????? ?????????, ????, ?????????? ???????? ? ????????????? ?? ???????.
futureactionnavigator.click – Guidance emphasizes planning ahead and executing steps purposefully for meaningful results
Strategic execution hub – Encourages organizing actions and maintaining focused progress
growthopportunitytracker.click – Motivating platform supports recognizing opportunities and taking strategic action confidently
discover growth lanes – Reading this feels inspiring and simplifies navigating opportunities.
?? ????? ?? ?????
intentionalgrowthpath.click – Insightful guidance helps maintain attention on priorities while progressing efficiently
progressive learning roadmap – Guidance encourages practical and continuous growth.
actionpathfinder.click – Clear guidance supports mapping out actionable steps for consistent growth
?????????? ?????????? ?????? ?????? ??? ????
https://goldenlink.club/felixschnaars
Strategic planning platform – Encourages careful planning for meaningful forward motion
practical learning tips – It made understanding the concepts much easier through relatable examples.
????? ?????? ????? https://unitalm.ru “??????-?” ???????? ???????? ?? ?????? ????? ????? ??? ?? 350-?? ??????????, ? ??? ????? ?? ??????????????????? ? ???????? ????????????. ? ????? ????????? ?????? ??????????????????? ? ????????? ???????????? ? ??????????? ?????? ?????.
Forward direction guide – Inspires quick exploration of strategies to advance goals efficiently
????? ?????????? ????????? ??? ??????? ????? ?? ?????-?????????? ? ???????. ????????? ???????? ???????? ????, ?????????, ????????. ????????? ????? ??? ? ???????, ?????? ? ????????/???????. ?????????? ????, ??? ???????????.
???????? ???????????? ?????? ???????????? ? ?????? — ??????? ??????? ????????? ???? ?????? ? ????? ????????? ????? ? ????????? ?????????. ????????? ??????, ??????, ???????, ?????, ??????, ????, ?????, ?????? ? ???????? ?????????. ???????? ????? ? ?????? ?? ????. ?????? ?????, ??????????????????.
focusedgrowthhub.click – Practical guidance supports following structured steps to achieve consistent progress
Focused innovation guide – Supports developing concepts with a clear direction and plan
pathwaytoopportunity.click – Guidance promotes discovering valuable opportunities and taking focused steps forward
Phase advancement hub – Encourages recognizing opportunities and acting on them effectively
startnewjourney.click – Focused tips help identify and take the next logical steps with confidence
progress roadmap tips – Advice supports structured, step-by-step execution.
Strategic learning hub – Offers guidance to apply insights carefully for better outcomes
focusandgrow.click – Clear advice promotes achieving steady progress by taking deliberate steps
future strategy ideas – The content encourages imaginative approaches to planning ahead.
Progress Path Portal – Provides guidance for designing effective steps to move forward confidently.
innovationexplorer.click – Insightful tips help discover creative solutions and fresh approaches
goal clarity guide – Advice provides clear direction and practical execution steps.
?? ????? ????? ????? ?? ?????
??????? ????? — ????????????? ???? ???????, ???????? ? ???????????????, ??????? ???????? ??? ????. ?????????????? ????? ?????????? ?????????? ?????????? ? ???? ????? ??? ????? ?????? ???????: ?? ????????????? ???????? ?? ??????? ???????????. ???????????????? ???????? ??????? ?????? ?? ????????? ???, ??????, ????????? ? ?????? ??????????? ??????, ??????????? ?? ??????? ?????????? ?????????. ??????? ????? ??????? ?????????? ?? https://www.florion.ru/catalog/buket-krasnyy ????????? ????? ????????? ??????? ??? ?????? ??????????. ???????? ?? ?????? ???????? ??????????, ???????? ???????? ? ??????????? ??? ??????? ???????? ?? ??????? ????????.
smart growth insights – A helpful space that delivers practical advice with an encouraging tone.
innovationstrategynavigator.click – Practical content highlights approaches to implement growth strategies successfully
Achievement learning hub – Encourages consistent practice and application to progress steadily
purposefulgrowthmap.click – Practical advice supports taking deliberate actions for significant and measurable progress
Goal-oriented focus guide – Encourages deliberate attention to key objectives
?? ????? ?? ?????
a href=”https://createimpactplanningframework.click/” />Impact planning hub – Provides tools to design and implement strategies that deliver real results efficiently
clearprogresspath.click – Inspiring guidance promotes building structured momentum with clarity and precision
potential achievement guide – Tips feel practical and can be applied without delay.
structuredgrowthideas.click – Organized planning ensures smooth and steady business expansion
executioninsights.click – Practical content helps plan, learn, and act with confidence for meaningful outcomes
innovative focus guide – Advice helps clarify ideas and maintain productive focus.
discover future paths – Inspires exploration and thinking beyond current approaches.
assured growth path – Suggestions are steady, clear, and motivating.
Inspirational direction hub – Offers ideas that guide progress naturally
freshgrowthinsights.click – Clear advice encourages identifying innovative approaches to achieve measurable success
breakthroughpathhub.click – Structured guidance encourages spotting pivotal moments that drive meaningful results
focusedgrowthnavigator.click – Guidance encourages users to start growth initiatives with clarity and strategic intent
Purposeful action hub – Encourages focusing on steps that create real impact
???????????????-??????????? ???????? «????????-?????» ?? ????????????? ???????????????? ?? ??????????? ?????????? ???????? ??? ??????? ? ???????? ????? ?????????. ?? ????? http://express-svyaz.ru/ ???????????? ?????? ?? ??????? ? ???????????? ?????? ???????????????, ?????????, ???????-???????? ????????????, ???? ? ????????????, ? ????? ?????????????? ? ???????????? ??????????????????, ????????? ?????? ? ???????? ??????. ???????? ???????? «??? ????», ??????? ?????????? ?????????? ? ??????????? ????????????, ??? ????????? ?????????? ???????? ???????? ?????????????? ? ??????? ??????? ? ?????????? ????????.
clearactionsteps.click – Insightful guidance helps turn plans into a structured path for achieving success
???????? «???????????» ?? ???????? ???????????? ??????????? ???????????? ?????-???? ? ???????????? ??????? ?? ???????? ??? ?????????? ? ??????????? ??????????. ??????????? ? ???????????? ?????? ????????? ??????? ????? ?????????: ?? ?????????????? 3D-?????? ?? ??????? ????????? ????????????. ????????? ? ???????????? ? ?????? ???????? ????? ?????? ?? https://press-forma.by/ – ????? ???????????? ??????? ?????, ??????? ??????? ???? ? ??????? ??????????????. ??????? ???????? ???????? ?????????? ??????, ????????????? ??????????? ??????? ? ?????? ? 2-3 ???? ???? ?? ????????? ? ????????? ?????????????.
create focused impact – The guidance simplifies decision-making and strategic focus.
sustainable progress ideas – Content encourages consistent, manageable development.
streamlined growth guide – Content feels structured without being overwhelming.
refineandgrow.click – Focused guidance ensures consistent improvement and strategic growth
productive focus tips – Encourages practical steps to stay attentive and organized.
forwardgrowthpath.click – Practical guidance promotes taking steady, actionable steps for growth
?????????? ?? ?????? ????? ????? ?? ????? ???????? ?? ???????: ??????? ?????????????????, ???????? ???? ????? ?? ??????? ????????????.
Forward action blueprint – Supports confident execution without overcomplication
growth direction roadmap – Practical examples give clarity and make progress easier.
fresh momentum source – Some points stood out as genuinely inspiring and easy to reflect on later.
achieve goals guide – Well-structured advice makes implementing strategies straightforward.
style-driven brand site – The designs show originality and confidence.
nextgrowthsteps.click – Strategic tips help uncover innovative ways to move forward smoothly
OMD Adventures – Smooth interface, content is enjoyable and simple to read.
step-by-step growth guide – Tips help implement strategies confidently and efficiently.
funwithfloralcow – Light-hearted content, pages are engaging and delightful to explore.
approach mastery guide – Insights help develop skills gradually and effectively.
artful growth concepts – There were ideas that sparked curiosity and fresh thinking.
???? ? ??? https://auto.ae/rent/car/ ??? ????: ??????? ????? ? ?/? ???????????, ??????????? ????? ????????, ??????????? ? ?????????. ?????? ?? ????? ? ?????????, ??????? ???????. VIP ???????? ????? — ?????? ?????????, ????, ?????????? ???????? ? ????????????? ?? ???????.
strategic exploration tips – Content motivates thoughtful action toward fresh possibilities.
???????? «????????» ???????? ?? ????? ?????????????? ? 2005 ???? ? ?????????? ?????? ???????? ????? ????? ????????? ?? ????? ?????????????. ? ???????? https://www.trub-prom.com/ ??????????? ??????? ??????????? ?????????: ?????????, ??????????????, ???????????, ????????? ????? ????????? ????? ????? ? ????????????. ??????????? ????? ??????-????????? ???????? ?? ?????? ? ??????? ? ???????????????? ? ????? ?????? ??, ??????????? ???????????? ?????????? ? ??????? ???????? ?????????.
ideaactionplanner – Clear direction, supports planning and executing ideas successfully.
modern apparel ideas – Everything feels cohesive and creatively executed.
Structured Action Hub – Guides users to map out clear strategies and optimize outcomes.
goalmappingtips – Practical insights, helps break down goals into manageable steps efficiently.
leverageyourplan – Useful content, encourages finding smart ways to advance plans with advantage.
OMD Lifestyle Journal – User-friendly, navigating posts feels clear and effortless.
growth opportunity insights – It comes across as a thoughtful place for intentional personal improvement.
quirkyfunmint – Delightful site, pages feel playful and creatively engaging.
clarity in progress – Advice is easy to understand and apply for steady advancement.
?????????? ???????? ?????????????? ???? ??????? 5 ?????? — ??????????? ????? ??? ???, ??? ????? ???????? ???????? ? ??????????????? ??? ?????? ????????. ????? ?????? ??????? ??? ????????? ??????, ?????????? ???????, ???? ??? ????????? ????????????? ??? ??????. ? ???????? ???????????? ?????????? ????? ?????? ????: «????????», «BabugenT», «?????», «?????? ???????» ? ??????? ???? «??? ????». ??????? ????? ?????????????? ???? ???????? ?? https://voda-s-gor.ru/butilirovannaya-voda/ ? ????????? ?? ????????? ? ?????????. ??????? ??????? ????????? ?????? ????? ??? ????? ????? ?????? ???????? ????, ? ???????? ???? ?????? ?????? ? ???????? ????????? ??? ?????? ?????.
?? ????? ?? ?????
strategic vision tips – Content encourages organized and actionable long-term planning.
fromideastomotion – Motivating insights, helps bring ideas to life with practical steps.
innovative thinking guide – Insights encourage practical creativity and fresh approaches.
creative hawaii hub – An inspiring space that highlights collaboration and talent.
directiondesignhub – Inspiring advice, shows how to structure objectives with clarity and focus.
leverageinsights – Helpful tips, demonstrates ways to make actions more effective with strategic leverage.
Rebecca Manzanita Notes – Engaging and authentic, site content feels personal and approachable.
??????? https://nazenazeblog.com/ ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
EveningGlowPDX – Engaging layout, site feels vibrant and easy to explore.
practical growth execution – Advice is concise and helps maintain focus while executing tasks.
discover next steps – Insights inspire planning and taking meaningful actions.
growthvisionhub – Practical guidance, helps visualize and act on growth paths effectively.
cs nippon knowledge base – Offers clear explanations without unnecessary complexity.
systematicprogress – Engaging tips, provides methods for moving forward with clear structure.
Hope & Lace online – Elegant presentation, navigation is intuitive and enjoyable.
????? ????????? ?? ????? ??????? ????????: ???????? ????????? ??? ????????.
proactive growth roadmap – Helps users begin initiatives efficiently and purposefully.
AppyTruckCreations – Innovative visuals, browsing the site is entertaining and appealing.
next step growth ideas – Advice is well-organized and encourages consistent improvement.
actionplannerpro – Motivating tips, helps maintain focus while executing efficiently.
Nu Soul Live Shows – Pleasant layout, event posts are simple to navigate and understand.
discussion engagement network – A steady flow of balanced topics and calm exchanges.
thoughtfulprogress – Encouraging insights, supports advancing with clarity and purpose.
focusdrivenframework – Motivating content, helps maintain clarity and direction while taking steps forward.
execution efficiency strategies – Offers tips for managing tasks smarter and faster.
ServiceMemberRelief – Positive initiative, guidance feels straightforward and engaging.
?????????????? ???? ?????????????? ???? .
planandprogress – Encouraging advice, keeps the focus on logical next actions efficiently.
Pro Wrestling AC – Well-organized pages, following news and matches is very convenient.
???????? ????? ? ??????????????? ?? ???? rulonnye-shtory-s-elektroprivodom71.ru .
????????????? ???????? ???? rulonnye-shtory-s-upravleniem.ru .
a href=”https://hanayaka-na-life.com/” />hanayaka daily inspiration – The presentation stays smooth and enjoyable.
??????????? ?????? ???????? ???????? ? ?????? internet-prodvizhenie-moskva3.ru .
?????? ??? ???? ? ??????????????? ?????? ??? ???? ? ??????????????? .
seo partner program internet-prodvizhenie-moskva2.ru .
growthmindengine – Useful insights, makes managing progress and focus simpler and more intentional.
Clarity Map Portal – Guides users to highlight areas for improvement and take structured steps forward.
????????????? ?????????? kupite-elektrokarniz.ru .
?????????????? ?????? ? ??????????????? ????????? zhalyuzi-elektricheskie.ru .
???????? ????? ?????? ?? ???? ???????? ????? ?????? ?? ???? .
ideastorealworld – Insightful tips, provides steps to implement ideas effectively and efficiently.
?????? ?? ????? ?? ?????
actionorientedclarity – Very actionable, helps prioritize and execute tasks efficiently each day.
Mac Office Lounge – Engaging and friendly, content is well structured and approachable.
goal-oriented insights – Encourages deliberate steps and thoughtful foresight in planning.
goaldrivensuccess – Clear strategies, content makes pursuing goals organized and actionable.
? ????? ???????? ?????????? ???????? ?????????? ??????? ?????????? ??? ???????? ????? ?????? ?????????????, ? ?????? ??????? ?????? ??????? ?????????? ??????????? ???????????? ??? ???????????? ???????????. ????????? otzivi.online ?????????? ?????? ???????? ?????? ? ???????, ??????? ? ????????? ? ????????? ?????? — ?? ???????????? ? ????????? ?? ????? ???, ????????? ??????????. ??????? ????????? ???????? ????????? ?????? ????? ?????? ??????????, ? ??????????? ????????? ??????????? ???? ? ??????????? ? ?????????? ?????? ?????? https://otzivi.online/ ????? ????????????? ??? ?????? ??????. ????? ????? ?????? ? ???????? ???????????? ? ??????????? ??????, ???????? ????????? ?????? ? ??????? «???????» ??? ???????? ???????????? ?? ???????? ????? ????? ?????? ????????, ??????? ?????? ? ??????? ????? ?? ?????? ??????????? ???????.
handcrafted design work – Impressive visuals highlight skill and attention to detail.
actionplanmastery – Very practical, breaks down goals into clear and manageable actions.
makeideashappen – Motivating content, offers practical steps to bring ideas to fruition quickly.
progressdrivensuccess – Insightful tips, helps convert motivation into measurable forward action.
JoJo Anime 10th blog – Enthralling site, content feels fresh and entertaining for viewers.
???? ???. ???? ???, ??? ????? ??? ??????? ???? ???, ???? ???????, ?????? ?????? ????, ?? ?? ?????? ?????. ?? ??? ????? ????? ?? ???????? ‘ ?? ?????? ??? . ??? ????? ????? ????, ????? ????? ???? ????. ??????, ??? ???? ???? ?? ?? ?????. – ??? ???? ??? ??? ?? ?? ?? ?? ???!? ????? ?? ???? ?????. – ??? ??????. – ??? ????? ???? ????. ??, ?? ?? ?? ???? ????. ??? https://mikhailpletnev.net
systematicprogress – Very insightful, ensures ideas move from concept to operational reality.
christmas themed fun – Browsing through it felt happy and relaxing.
intelligentactionplan – Practical content, encourages careful steps toward achieving meaningful goals.
???? ? ??????? ????? ?? ????? ?????: ?? ??????? ?? ??????????????? ???????? ?? ????? ??????.
?????? ?????????????? elektrokarnizy4.ru .
clarity-driven roadmap – Encourages planning and acting with clear intent.
limitlessideas – Engaging tips, inspires exploring new concepts without restrictions.
?????? ?????? https://everumonline.ru ???? ?? ?????????? ???????????, live-??????, ?????? ? ???????. ?????????? ???????? ? ???????, ?????? ? ???????? ?????? ????? ?????. ?????? ???????? ??????, ????????? ? ?????? ???????.
???????? ????? ? ??????????????? ?? ???? rulonnye-shtory-s-upravleniem.ru .
???????? ?????? ????? internet-prodvizhenie-moskva3.ru .
??????????? ????? ? google internet-prodvizhenie-moskva2.ru .
???????? ????? ??????? ???? ???????? ????? ??????? ???? .
how to email bomb an email address
Email Bombing – email flood or email hoax (DOS attack) or cluster email bombing, what are they actually doing?
A huge number of emails are sent to e-mail. This usually means that the @Flood_email_bot specifically targets the victim’s mailbox associated with your email.
These emails are intended to make fun of friends or distract the victim from any security messages or other emails.
I am glad to present you a mail flood bot with a convenient menu and flexible settings!
The cost of the service is $ 1 = 1000 letters.
You specify the time of the flood and the number of letters yourself, or choose the “FAST FLOOD” function
During the flood, a sufficient number of letters arrive so that the owner would miss an important letter!
The bot will flood more than you ordered. On average, 30% more than ordered.
Flood email, Floods Email, Email flooding, gmail flood, email bomber, flood hotmail, flood online,email flooding, email flood bot, email flooded with spam, email flooding service, email flooded with subscriptions, email flooder bot, email bomber 2023, email bomber 2024, email spam bot online, email spammer bot free, spam bot, ??? ?? ????? ????, ?????? ?? ????? ????, ?????? ?? ?????, ???? ??????.
@Flood_email_bot – ?????? ????? ?????? ?? ?????!
Sega Live Central – Interactive and fun, navigation is smooth and content feels lively.
effectiveoutcomedesign – Insightful guidance, encourages structured approaches to reach objectives.
????? ???????? ????? ????? ???????? ????? .
strategicclarityhub – Encouraging insights, demonstrates ways to plan and act effectively today.
riobet casino ?????? ?????? ????: ??????? ?????? ? ????? ??????? ????? ???? ? ?????? ?????? ?????????????? ? ??????? ?????? ? ??????, ????????? ??? ???????????. ????? ????? ?? ?????? ????? ?????????? ? ????, ????????? ???? ??? ??????? ???????.
precisioninaction – Very practical, guides on prioritizing tasks for optimal results.
discover bloemhill – Visually appealing content that delivers the message with clarity and style.
?????? ??? ???????? ?????? ??? ????????: ??????? ? ??????????? ??? ????? ?????? ??? ???????? – ??? ????????????? ??????, ???????????? ??? ???? ???????, ??????? ?? ??????? ?? ?????? ???????? ????????.
focusedcreativity – Very helpful, demonstrates how to prioritize efforts for maximum impact.
????????????? ????????? zhalyuzi-elektricheskie.ru .
?????????????? ?????? ??? ???? kupite-elektrokarniz.ru .
?????????? ???????? ???? shtory-s-elektroprivodom-rulonnye.ru .
focused clarity tips – This helped simplify complex decisions for me
Battle Begins Store – Neat layout, merchandise is easy to browse and visually appealing.
intentional action guide – Encourages taking focused steps on your ideas without delay
?????????? ??? ????? 7 8 ???
focusedenergyflow – Useful advice, makes managing energy and progress feel simple and structured.
plan your path – Practical advice on defining steps for measurable progress
?????? ?????? https://riobetmobile.ru ??????, ????? ? live-????, ???????, ????????? ??????, ???????????, ?????? ? ???????. ???? ?????, ???? ????????, ? ???-????, ?? ??? ???????? ???????? ????? ??????????? ? ?????. ????????? ?? 2025.
clear results guide – Offers practical tips to focus efforts and achieve tangible outcomes
Mi ar?yorsunuz lisansl casino turkiye? Sekabet Casino Türkiye’ye eri?mek, kay?t ile para yat?rma/çekme ad?mlar?n? ö?renmek ve önde gelen yaz?l?m sa?lay?c?lar?n?n oyunlar?yla spor bahislerini ke?fetmek için villaperret26.com ziyaret edin. Bonuslar ve promosyonlar, cömert ödüllerle zengin bir program sa?lar. Mobil uygulamam?zla diledi?iniz yerde oynay?n — basit arayüz, tüm cihazlara h?zl? kurulum.
stepbystepclarity – Motivating guidance, helps convert plans into actionable progress effectively.
thinkforward – Shares strategies that help make ideas actionable and productive.
perfectfinds – Makes discovering bargains fast, easy, and convenient.
vineyard wedding tips – Clear and attractive visuals, planning content is easy to understand.
creativeenergyflow – Encouraging content, makes finding inventive solutions more accessible daily.
growthblueprint – Motivating advice, outlines ways to organize efforts and track consistent progress.
????? ??????? ??????????? ??????? ??? ????, ???? ? ?????????? ?? ???????? ?????? ???????? https://becompact.ru/ – ? ??? ????????? ??????? ?? ?????? ????? ? ??????? ????????? ?? ??????. ?????????? ??? ???????, ? ??? ?? ??????? ??? ?? ??????? ??? ?????????? ? ?????????????? ?????????? ?? ??????????? ?????? ? ??????????? ????????????.
Invest in Mali insights – Practical advice, content is professional and well-organized.
????????????? ???????? elektrokarnizy4.ru .
actionable thinking – Makes it easy to turn abstract concepts into practical tasks
ClarityInMotion – Easy guidance, supports moving forward with confidence and direction.
???????
step by step clarity – Helped me break down actions and plan effectively
?????? ?????? ??????????? ?????? ?????? ???????????: ???????? ????? ? ??? ???? ??????? ??????????? ? ?????? ?????? ????? ? ???????? ????? ????????? ?????. ???????????????????, ?? ????????? ?????? ?? ???? ?????, ??????? ? ??????, ???????????? ??????.
impactfulideas – Practical content, supports implementing thoughts that matter effectively.
goal oriented clarity – Encourages planning and acting with clear intent to succeed
savvyshopper – Provides a streamlined way to find the best deals efficiently.
??????? ???????? ????? ?????? ? ?????? ??????? ???????? ????? ?????? ? ?????? .
focused path guide – Encourages creating a roadmap that keeps progress steady
lifelaunch – Provides strategies to move from ideas to impactful outcomes efficiently.
??????????? ? ??????????? ?????? ?????? internet-prodvizhenie-moskva3.ru .
????????? seo ? ?????? internet-prodvizhenie-moskva2.ru .
????????????? ?????? ?? ??????????? ?????? ??? ????????: ??????? ? ??????????? ??? ????? ?????? ??? ???????? – ??? ????????????? ??????, ???????????? ??? ???? ???????, ??????? ?? ??????? ?? ?????? ???????? ????????.
envolavecning reference – Well-organized sections make browsing comfortable.
manageablegrowth – Motivating guidance, helps turn complex projects into achievable, stepwise actions.
???????? ????? ? ??????????????? ?? ??????????? ???? rulonnye-shtory-s-elektroprivodom71.ru .
valueactions – Provides advice on turning simple efforts into meaningful outcomes.
focuseddirection – Inspiring guidance, helps channel energy toward meaningful actions effectively.
??????????? ???????? ? ?????????? ????????? ???????????????? ???????? ?????? ?? ????????, ????????, ????????????? ? ??????????? ?????? ? ????? ??? 10-?????? ?????? ??????. ?? ????? https://yuridicheskaya-kompaniya-krasnodar.ru/ ???????? ?????????? ????????? ???????????? ? ???????? ?????????? ? ?????????? ????. ??????????? ???????????? ???????? ???????? ?? ???? ???????? ??????????, ???????? ?? ???????? ? ????????? ??????? ? ??????????? ????????????????? ??????? ???????? ???????? ????? ?????????.
????????????? ?????? ????????? ?? ??????????? ? ?????? ? ??????? ??? ??????????
alignmentforprogress – Actionable advice, ensures daily efforts contribute to bigger goals.
make visions happen – Shows how to move from planning to real-world execution smoothly
happypicks – Combines cheerful design and easy navigation to make product discovery fun.
progressionplanner – Encouraging tips, keeps the focus on structured and measurable advancement.
????? ????? ????? ????? .
goalprogress – Encourages consistent habits that contribute to meaningful achievements.
barnhouse-pod-kluch.ru
stay on track guide – Encourages structured approaches to avoid unnecessary diversions
actionwithclarity – Practical strategies, shows how to execute objectives with precision and purpose.
practicalvalue – Offers advice for extracting usefulness and benefit from daily routines.
steady progress habits – Focuses on maintaining balance while moving forward
deliberate action roadmap – Offers guidance for maintaining direction while growing effectively
??????? – ??? ??? ???? ????????, ???????????? ??? ??????????? ???? ?????????? ?????????. ???????, ??? ?? ??? ?????????, ???????, ??? ?? ?????? ?? ???? ???? ?????????? ???? ?????? ? ????????????. https://pokerbonuses.ru/download/index.html
bizlinkworld – Offers a dependable platform with clear guidance for networking and professional growth.
?????? ??? ???? ????????????? ?????? ??? ???? ????????????? .
motion focused strategies – Practical tips to ensure progress doesn’t slow down
?????????????? ?????? ? ??????????????? ?? ???? ?????????????? ?????? ? ??????????????? ?? ???? .
reliableshopper – Makes browsing simple while offering trustworthy product details for buyers.
?????? ??????????????? ???? ?????? kupite-elektrokarniz.ru .
???????? ????? ? ??????????????? ?? ???? shtory-s-elektroprivodom-rulonnye.ru .
seek and advance – Encourages exploring new chances and moving forward decisively
attentionfirst – Highlights how proper focus enhances performance and outcomes.
?????? ? ????????????? ??????? ??????? ?????? ? ?????????????? ???????? – ??? ???????? ?????????? ??? ?????? ???????????? ???????? ???????, ????????????? ????? ???????? ??????? ??? ???? ??? ???????? ? ??????????????? ??????? ?????????.
???????? ?? ????????????? ????? ????????????? ????????: ?????????? ???????? ??? ????????? ????????? ?????? ????????????? ???????? – ??? ???????? ??????????? ???????? ????? ? ??????? ??????, ?? ?????? ???????????? ??????????.
system design tips – Encourages organizing thinking into efficient and practical systems
ideas step forward – Encourages progress in a relaxed and clear way
???????? ????? ? ?????????????? ??????????? rulonnye-shtory-s-upravleniem.ru .
future roadmap ideas – The guidance helps organize ideas and plan effectively.
???????????? ?????? ????? ???????????? ?????? ????? .
??????????? ????? ??????? internet-prodvizhenie-moskva2.ru .
telegram z kraken
???????? ????? ??? ???????????? ???????? ???????????? ? ???????????????. ??????????? ??????????, ????? ??? ????, ?????? ? ???????, ??????? ???????? ??????, ???????????? ??????????? ? ????????. ?? ?????? ???????????? ???? ??? ?? ???????, ??? ????????? ? ????????. ?????????? ????????????? ???????? ????? ??????, ???????? ?????????? ? ?????????? ????????. ??? ???????? ???????????? ??????? ????????? ??? ?????? ? ???? ? ??????????
matchfinder – Provides an organized way to discover items and content suited to your tastes.
?????????? ?????????? ??????????? ?????? — ??? ????????
https://linknest.vip/magnolia42v246
????????????? ?????? ? ?????? ?? ???????????
forwardguidance – Helpful perspectives show how guidance fuels steady daily progress.
toptrendingbuys – Presents top products in a way that makes shopping fun and simple.
purposeful progress tips – Offers practical guidance for staying focused and moving forward steadily
claritymindset – Highlights the advantage of a clarity-first approach in daily decisions.
successclarity – Helps align daily decisions with long-term growth goals.
????? ????? ????? ????? .
executionfirst – Emphasizes that taking initiative builds confidence and tangible achievements.
practical buying guide – Encourages quick and informed decision-making with clarity
intentionalgrowth – Shows that purposeful attention ensures meaningful and consistent advancement.
wisdomshare – Encourages users to share insights and grow together in a supportive community.
progresswithclarity – Demonstrates how clear direction keeps actions consistent and impactful.
measured advancement guide – Encourages deliberate and precise action toward goals
forwardwithdirection – Useful advice, emphasizes that building direction first results in focused and actionable growth.
???????? ????? ????? ?????????? ??????????? ??? ??? ???????? ????? ?????, ??????????? ???????????? ?????????? ????? ? ????????? ????????? ????? ?????????? ??????????. ????????????-?????????? ???? ?????????? ??????????? ?????? ? ???????, ????????? ???????????????? ????????????, ????????????????? ???????? ? ???????????? ???????? ??? ????????? ?????????? ????? ? ??????? ??????????. ????????? https://rodinasportsclub.com/ ????????????? ?????????? ? ????????? ???????????? — ?? ??????? ?????????? ? ?????????????? ?? ????????? ??????? ? ????????????? ????????. ???? ??????? ?????????? ????????? ??? ?????????? ?????????? ?????, ???? ?? ???????? ????, ??????????? ???????? ????? ??? ?????? ??????????? ??????, ????????? ??????? ?????????? ? ?????? ??????? ??????????? ??? ?????????? ???????????.
plan with purpose – Encourages deliberate thinking prior to taking action
??????
clearpathforward – Emphasizes making decisions based on clear priorities and insight.
actionwithstrategy – Motivating content, demonstrates that strategic steps produce sustainable results quickly.
directedgrowth – Actionable insights connect clear direction with reliable momentum.
????????????? ?????????? ?? ??????? ??????? — ?????????? ????????, ????????? ?????? ??? ??????????? ? ??????? ?????????? ????????? ??? — ??????? ??????? ??????? ? ???????? ??????????. ???????? ???? ??????????????? ???? ??? ????????????? ???????, ??????????? ????????? ????????? ??????? ??? ??? ?????????? ???????? ????? ? ??????????? ?????????? ??????. ??????????? ???????? ???????????????? ?? ???????????? ???? ????????? ????????? ?? 57 ?? 108 ??????????? ? ?????????????? ? ?????????????? ?????????????, ??????????????? ??? ?????????? ??????? ??????. ?? ??????? https://vintoviesvai64.ru/ ??????????? ??????????? ??? ??????? ???????? ????, ?????????? ??????????? ???????? ? ???????? ?????? ???????? ?? ???? ???????. ????????????? ????????????? ???????? ??? ?????? ????????? ?????? ??? ???????, ? ???????? ??????????? ???????????? ????????????? ???? ? ???????? ? ??????? ?????? ? ???????? ???????? ????????.
mindshift – Encourages constructive actions and personal growth strategies effectively.
momentumguide – Offers tips to sustain progress without losing focus or energy.
purposefulmovement – Useful tips, emphasizes that direction-focused actions generate reliable results.
resultswithconfidence – Emphasizes that carrying out plans consistently enhances confidence and produces measurable success.
momentum action plan – Encourages structured steps that generate quick results
strategic opportunity ideas – It makes evaluating future options much easier and actionable.
easy choice tips – Shows how to navigate choices quickly while accessing useful information
trendcentral – Makes exploring seasonal items fast, simple, and engaging.
?????????? ??????? ????? ??? ?????????? ??????? ????? ??? .
movementthroughclarity – Demonstrates that clarity helps maintain consistent and purposeful progress.
directionmattersfirst – Useful content, highlights that putting direction first creates meaningful forward momentum.
purposeledmovement – Shows that clarity creates smoother, goal-aligned progress.
execute efficiently – Provides guidance on turning ideas into actionable steps seamlessly
worktowin – Reinforces that outcomes are earned through continuous action.
hotpicks – Keeps shoppers entertained while discovering trending products.
mindfulprogress – Encourages deliberate actions that lead to measurable outcomes.
purposeledexecution – Demonstrates that focused execution ensures consistent forward movement.
?????? ? ?????????????? zhalyuzi-elektricheskie.ru .
??????? ??? ???? ?????? ? ?????? ??????? ??? ???? ?????? ? ?????? .
???????? ????? ????? ???? shtory-s-elektroprivodom-rulonnye.ru .
actionleadsforward – Highlights that guided execution results in measurable growth and achievement.
idea execution help – Advice here sounds straightforward and usable without confusion
targeted action plan – Practical ideas for aligning daily steps with larger objectives
forwardclarity – Motivating content, highlights that progress aligned with direction ensures consistent outcomes.
unique items navigator – Encourages a smooth and fun browsing experience for standout products
latesttrends – Provides a lively platform for discovering current popular items.
????? ??????? ??????? ??????? ????????? ? ??? ???????? ????? ??????? ???????? ????????????? ? ????? ?? ????? promo.eatvio.ru – ??????? ?????????, ???????????? ?????? ? ???? ???????, ??????, ????? ? ?????????. ???? ?????????? – ?? ??????? ??????? ?? ?????? ??????????? ???????? ??????????, ?????????? ???????? ??????? ? ??????? ? ???????? ????????, ? ?? ? ??????. ??????? ??? ??????????? ?? ??????? – ?? ????? ???????! ??? ???? ? ??????????? ???? ?????????? ?????!
actionforideas – Useful tips, emphasizes that ideas gain value only when executed purposefully.
intentionalsteps – Shows how deliberate direction ensures every action counts toward goals.
goalorientedideas – Highlights the value of directing ideas toward achievable outcomes.
planningwithvision – Highlights how forward-thinking ideas simplify progress.
thoughtpath – Shows how giving ideas direction ensures they lead to meaningful results.
claritydrivesaction – Demonstrates that attention and focus create actionable outcomes from ideas.
maintain focus guide – Highlights ways to sustain attention to achieve consistent progress
wise execution guide – Offers practical tips that can be applied right away.
toptrendsnow – Simplifies shopping for trending items with a clean, user-friendly interface.
??????? – ??? ?? ?????? ????????? ????, ??? ????? ????????? ??????, ????????? ? ??????????, ?????? ????? ???????????. ???????? ??????? ?? ????? ???? ????????? ?????????? ?? ???????????? ???????, ????? ???????? ????? ? ?????????????????? ???? ??????. ??????? ?????????? ??????? ????? ???????? ? ???????, ?? ????????????? ?????????? ??????? ?? ????? ???????????? ??????????????, ???????????? ??????????? ??? ??????????, ??? ? ??????? ???????. https://pokerbonuses.ru/download/index.html
intentionalgrowth – Highlights that clarity in direction promotes meaningful and steady progress.
growthguide – Provides guidance for improving professional skills and achieving career goals.
turn thoughts into tasks – Clear direction for making ideas tangible and doable
gift selection guide – Shows practical ways to choose gifts quickly and confidently
momentumpath – Shows how clarity in direction maintains a steady flow of progress.
momentumbydirection – Motivating content, highlights how intentional direction accelerates movement and achieves results.
?????? ???? ?????????????
???????? ????? ??? ???????????? ???????? ???????????? ? ???????????????. ??????????? ??????????, ????? ??? ????, ?????? ? ???????, ??????? ???????? ??????, ???????????? ??????????? ? ????????. ?? ?????? ???????????? ???? ??? ?? ???????, ??? ????????? ? ????????. ?????????? ????????????? ???????? ????? ??????, ???????? ?????????? ? ?????????? ????????. ??? ???????? ???????????? ??????? ????????? ??? ?????? ? ???? ? ??????????
clearlydefinedideas – Motivating content, emphasizes that well-defined ideas achieve better results.
clear action steps – Helpful reminder that clean strategies can still be powerful
?????? ?????? ?????? ??? ???????? ? ??????? – ??? ??? ????? ??????????????? ???????????. ???? ??????????? ?? ?????? ???????, ?? ? ??????? ?????????? ???????? ??? ???????????????? ?????????? ????? ?????? ??????? ?????????, ????? ???? ???????. ????? ???????, ??? ????? ??????????? ?????? ????????? ? ????????????? ????????? ? ?????????????, ? ??????? ??????? ?????? ???????.
concentratedgrowth – Motivating content, emphasizes that clear focus fuels continuous personal and professional growth.
intentionalsteps – Encourages making steady progress through thoughtful and pressure-free actions.
focuspathway – Provides insights on channeling energy toward consistent improvement.
clearstepsforward – Emphasizes that a focused plan promotes steady and meaningful outcomes.
clarityempowers – Emphasizes that clarity fuels intentional and effective actions for continuous advancement.
growth with structure – Offers practical tips for creating sustainable and measurable development
easyfinds – Simplifies browsing so visitors can locate items without confusion.
journeylaunch – Helps users start new ventures with clarity and enthusiasm.
stepbyintent – Highlights that mindful actions create a reliable path to progress.
smart outcome building – Offers clear steps for producing noticeable progress
trend insights guide – Offers clear and engaging ways to explore current global trends
focusbeforegrowth – Useful guidance, emphasizes that establishing clarity first sets the stage for sustainable growth.
continuous growth guide – Ideas feel motivating and help maintain consistent effort.
ideasintoreality – Motivating content, shows how executing ideas creates real, measurable results.
conceptgrowth – Shows how ideas evolve into progress through focused effort.
forwardwithclarity – Emphasizes that clear planning fuels steady, measurable, and intentional progress.
momentumguide – Provides insights for keeping work flowing with clarity and purpose.
resultsdrivenfocus – Useful advice, demonstrates that clear focus transforms effort into actionable and effective outcomes.
ShowStaff https://showstaff.ru/ – ?????? ????????? ? ??????? ????! ???????? ????, ??? ?? ??????? ????, ?????????? ?????????, ?????????? ?? ?????????? ? ?????????? ?????. ?????? ?????????? ? ???????????. ?? ?????? ??????? ????? ??? ??????????? ? ??????, ??? ? ? ????????? ?? ????? ????! ?????????? ???????, ? ?? ??????? ??? ???? ???? ?? ??????? ????????!
progress with freedom – Motivation here feels flexible and empowering
plannedsuccess – Shows how deliberate steps turn objectives into tangible achievements.
lifeupgrade – Offers simple tips to make routines more productive and enjoyable.
actiondrivesclarity – Useful guidance, shows how deliberate action helps clarify priorities and plans.
smilecart – Delightful shopping experience that feels welcoming and effortless.
plannedgrowth – Emphasizes how structured direction drives impactful growth.
strategic direction tips – Guides on prioritizing direction before speed for better results
focused progress path – Shows how deliberate steps lead to real accomplishments
aligneddirection – Inspiring tips, shows that alignment with direction creates measurable and meaningful progress.
bestdealsforlife – Practical offers, content feels reliable and makes finding deals effortless and convenient.
takeactiontoday – Demonstrates that acting instead of overanalyzing maximizes efficiency and outcomes.
actionplan – Emphasizes how taking guided actions ensures measurable success.
structuredgrowth – Explains how organization plays a key role in building momentum.
smoothprogress – Shows ways to maintain consistent momentum through clear planning.
???? ?????? ????? ????? ?? «???????? ??????», ? ???? ?????? ? ????????? ? ??????, ????? ???????, ??????? ????? ???????? ? ??????????, ????????? ? ???????????? ???????? ??? ? ?????? ????????. ?? https://seoprofi.org/ ?? ??????? ???????? ?????? ? SEO: ?????, ?????????? ????? ? ????????????? ? ??????? ?? ????????? ?????????. ??? ??????? ??????? ??? ???????, ??????? ????? ???????????? ? ?????.
ideasmadeaction – Shows that acting quickly on concepts leads to tangible and fast results.
projectignite – Motivates starting projects with clarity, purpose, and confidence.
outcomefocused – Highlights the impact of clear direction on achieving successful outcomes.
goalorientedfocus – Motivating guidance, highlights that focusing on key objectives generates consistent and meaningful results.
results through action – Strong insight showing that outcomes improve when action stays consistent
progressive ideas page – It provides insights that make you rethink traditional approaches.
clarityguideschoices – Useful guidance, demonstrates that clarity allows more effective decision-making in complex situations.
think ahead effectively – Highlights ways to implement innovative methods in everyday projects
planning to execution – Guides on translating ideas into measurable progress
never stop learning – Encourages embracing curiosity and discovering new knowledge
realizeideas – Shows that implementing ideas strategically leads to continuous growth and observable results.
stepbystepgrowth – Shows that careful planning and execution build sustainable progress.
momentumpath – Provides tips for turning clarity into ongoing forward motion.
clearpathforward – Demonstrates how clarity simplifies execution and decision-making.
???????? «??????????????» ????????? ????????????? ????????? ???????? ? ??????? ???????? ?? ???????? ??????? ?? ?????? ? ??? ? ??????????. ???????? ????????? ??????, ??????????? ? ???????????? ??????: ???????? ??????, ????? ??????? ? ??????????, ????????, ??????, ???????, ???????, ????????? ? ?????. ???????????? ? ?????? ????????????? ????? ?? ????? https://skmetspb.ru/ ??????????? ???????????? ? ??????????? ????????-???????????????, ??????????? ??????? ???????? ????????? ? ????????????? ?????? ????? ? ???????? ???????.
dynamicideas – Emphasizes that taking steps forward for ideas leads to measurable impact.
momentumguide – Highlights the role of clear thinking in maintaining continuous progress.
????? ????????????? ?????????? ???? ??? ???? ? ?????????? ? ????????????? ????? ???????? ???? https://masterim-novostroy.ru/ – ?????????? ???? ??????? ? ??????? ??????? ?????? ??? ?? 2 ??????! ? ??? ????????????? ?? ????????? ????? ?? ???? ??? ????? — ?? ???????? ??????? ? ???????????? ?? ???????? ??????? ? ??????. ??????? ????????? ?? ????? ? ???????? ????? ????????? ? ?????? ????????????!
???????????????? ?????? ? ?????????? ???????????????? ???????? ??????? ???????????? ????????? ?????????? ? ????????????? ???????, ??????????????? ??????????? ??????????. ??????? ???????? ??????? ?????, ????????? ? ??????????? ????????? ???????????? ?????????????? ??????? ??? ?????? ????????. ???????? ?? ?????-?????????? ?????????? ??????? ??????????? ????????? — ?? ???????? ?????? ????????? ????????? ?? ???????????????? ?????? ??????? ? ???????? ????????. ?? ??????? https://nemans.ru/ ??????????? ?????? ??????? ??????? ??? ??????????? ????????, ???????, ???????????????? ????? ? ??????? ?????????. ?????? ?????????????? ? ??????????????? ??????????? ???????????? ????, ?????????? ??????? ??????? ?? ?????? ? ??????????? ???????????? ?????????????? ??????????? ??? ?????????? ???????? ? ?????? ????????? ?? ????????????.
turnideasintoreality – Inspiring advice, highlights how actionable steps transform ideas into real-world results efficiently.
Game-Lands https://game-lands.ru/ – ??? ???? ? ?????????? ??????? ? ????????????? ??? ???????? ? ??????? ???????. ????? ?? ??????? ?????? ??????, ??????? ????? ? ??????, ?????? ???????????? ?????????, ????????, ????????, ? ??????????? ????? ?? ???????. ???????, ??? ???????? ?????? ??????????, ??? ?????? ? ??????? ???????? ? ? ???? ?????? ? ????? ?????. ???, ????? ???????? ????? ? ???????? ??? ??????????? ??????? ???????.
planforwardeffectively – Motivating guidance, shows that effective forward planning reduces errors and increases efficiency.
focusedgrowth – Demonstrates how clarity in planning enhances both personal and professional progress.
forwarddrive – Useful insights, emphasizes keeping daily momentum alive for success.
forward looking insights – Strong logic ties each idea together smoothly
focusflow – Highlights how attention helps momentum develop naturally.
purposefulaction – Encourages taking steps that directly support your desired outcomes.
achieve through clarity – Motivates using clear strategies to create meaningful progress
strategicexecution – Emphasizes that clarity in direction ensures tasks are completed effectively.
?????? ?? ????? — ?????????? ?????????? ?????? ?????? ??? ????????
https://my70size.com/@garnetfreeling?page=about
strategic growth exploration – The content energized my thinking and motivated practical steps.
daily focus boost – Simple strategies enhance focus and reduce mental friction.
turn thought into action – Proper execution transforms vision into actual progress.
clarityforward – Motivating content, highlights how moving toward clarity with intention creates consistent results.
structuredprogress – Highlights that a guided execution path ensures steady forward movement.
keepmomentumflowing – Practical guidance, shows how small, deliberate steps maintain ongoing movement.
???????? ??????? ? ??????-????????? ??????? ????????? ?????? ? ??????????????, ???????? ???????? ??? ????????? ? ????? ???????? ??????? ???????? ????? ?????????? ????????????? ???????, ????????? ???????? ???????? ? ?????????? ? ?????? ???????
intentionalprogress.click – Engaging platform, ideal for exploring and developing fresh concepts.
brightvalueoutlet – Inspiring platform, helps users develop creativity and practical skills.
forwardmotion – Shows how continuous movement matters more than flawless execution.
??????????? ???????? ??????? ?? ?????? ??????????, ?? ? ?????????? ???????, ???????? ????? ???? ???? ? ?????????? ? ?????????? ?????????? ??? ?????????????? ?????? ????????????. ??????? ??????? ?? ???????? ? ????? ????????? ???????????? ????????? ?????????????, ???????????? ? ???????? ? ???????????? ???????????? ????????? — ?? ???????????? ?? ??????????? ?????? ? ????????? ???????? ??????. ????????????? ???????? ?????????? ??????? ????????? ?????????? ?????? ??????? ???? ? Cesal, ?????????? ??? ??????????? ???????? ??? ??????????????? ????????? ??? ??????????? ????????????. ?? ????? https://potolki-52.ru/ ???????? ??????? ??????????? ??? ??????? ????????? ??? ?????????? ??????? ?????????, ? ????? ????????? ???????? ????????????? ? ????????? ???????. ??????????? ??????????? ?????? ?? ???? ?? ?????? ??????????? ????????? ???????????? ??????????? ??? ????? ??????????? ??????? ???????? ??? ???????????.
growthbycreativedesign – Shows that combining design and strategy leads to consistent forward progress.
realistic progress strategy – The guidance avoids hype and feels dependable
focus-led results – Concentrated effort turns creative thoughts into measurable progress.
progressive action – Small, consistent actions compound into significant achievements.
planningforgrowth – Motivating tips, demonstrates that careful planning ensures sustainable and reliable growth outcomes.
steadyclarity – Emphasizes that keeping clarity in motion promotes reliable and meaningful progress.
actionable ideas – Acting on ideas carefully creates meaningful and measurable outcomes.
confusionfreechoices – Highlights that clarity provides a roadmap for better decisions every time.
strategy clarity insights – The content feels approachable and makes planning achievable.
progresswithintent – Emphasizes moving forward through purposeful daily actions.
focusonforward – Shows that structured building and guidance ensure steady forward momentum.
growthbyblueprint – Useful guidance, highlights how designing your steps leads to consistent forward movement.
attention drives results – Focusing your energy ensures ideas become effective solutions.
intentionalimpactgrowth – Useful tips, highlights that purposeful action drives meaningful and consistent progress.
plan and move – A strong strategy ensures energy is channeled toward progress.
steady growth path – Repetition of clear steps builds long-term progress effectively.
clarityatwork – Practical advice, shows how clear thinking and planning lead to impactful outcomes.
?????? ??????? https://casinobezdeposita.ru ?????? ?? ???????????, ????????, ?????????. ?????????? ??????? ????????, ????? ??????, ?????, ??????????? ? ?????????. ?????????? ? ??????? ?? ??????? ??????.
momentum mastery – Applying well-defined strategies drives ongoing progress efficiently.
??? ??????? ??????? ????????? ? ?????, ??? ?? ??? ??? ????????. ????? ???????? ???????? ??????. ????????: https://v-tagile.ru/obschestvo-iyul-5/kak-vybrat-takticheskuyu-razgruzku-poshagovoe-rukovodstvo-dlya-novichka
learn with purpose – The guidance encourages thoughtful and continuous development.
??????? ????? ??????
???????? ????? ??? ???????????? ???????? ???????????? ? ???????????????. ??????????? ??????????, ????? ??? ????, ?????? ? ???????, ??????? ???????? ??????, ???????????? ??????????? ? ????????. ?? ?????? ???????????? ???? ??? ?? ???????, ??? ????????? ? ????????. ?????????? ????????????? ???????? ????? ??????, ???????? ?????????? ? ?????????? ????????. ??? ???????? ???????????? ??????? ????????? ??? ?????? ? ???? ? ??????????
direction through clarity – When clarity guides actions, progress becomes measurable and steady.
All details at the link: https://lionth.org/777tha/
??? «???????????» https://www.trustsol.ru ?????????? IT-???????? ? ????? ??? 15-?????? ?????? ? ??????????, ????????? ? ????????????? IT-?????? ??? ???????. ???????? ?????????? ??????????? IT-??????????, ????????????????? ???????? ? ??????? ???????, ????????????, ?????????, ???????? ??????? ? ?????????? ??. ??????????? ??????????? ?????, ??????? ? ??????? ???????????, ???????? ?????????????? ??????????????, ??????? ???????? ? ?????????? ?????????? ?????? IT-?????.
steady advancement – Consistent forward action drives success and achievement.
????????????? ?????? ? ?????? ?? ???????????
??????????? ???????? ?????????? ??????????? ??????? ??? ?????? ? ???????? ????????? ? — ????????????, ??????? ?????? ????? ????????? ???????????. ??????????????? ???????? ?? ?????? ??????????? ? ???????????? ????????????? ??????? ????????????? ?????? ????????? ????????? ??????, ???????? ????????? ??????? ??????????? ????????????????? ??????. ????????? ?????????? ? ????????? ????????, ??????????? ????????????? ? ???????????? ?????????? ????? ????? ?? https://velkast.com/ — ??????????? ?????????????? ???????. ???????? ??????? ?????????? ???????????? ??????? ???????? ? ??????????? ?????? ?? ???????????? ?????-?????????? ????? ???????????? ???????????? ? ??????????? ???????? ??????.
intentionalfocus – Inspiring guidance, highlights how deliberate focus accelerates steady and sustainable progress.
careful execution – Each step, executed thoughtfully, ensures lasting impact.
confident steps – When clarity guides decisions, each step is taken with assurance.
growth direction ideas – Navigation is smooth, and the advice feels achievable.
innovate and execute – Transforming innovation into action produces tangible benefits.
Mi ar?yorsunuz sekabet casino? Sekabet Casino Türkiye’ye eri?mek, kay?t ile para yat?rma/çekme ad?mlar?n? ö?renmek ve önde gelen yaz?l?m sa?lay?c?lar?n?n oyunlar?yla spor bahislerini ke?fetmek için villaperret26.com ziyaret edin. Bonuslar ve promosyonlar, cömert ödüllerle zengin bir program sa?lar. Uygulamam?z mobilde her an eri?ilebilir; kullan?m? pratik ve tüm cihazlarla uyumlu.
confidenceinmotion – Useful guidance, shows that defined direction empowers confidence and encourages proactive steps.
???????? ???? ????? https://eicom.ru/ ? ?? ??????? ?????? ??????????? ??????????, ??????? ? ??????????? ? ??????? ???????????? ? ?????????? ????????? ?? ??????. ? ??????? ????? 10 000 ???????. ????????? ????? ???????????. ???????????? ? ????? ?????????????, ? ?? ??????????? ??????? ??? ???? ??????????? ??????????, ???????????, ????, ???????, ?????, ????????????, ?????????, ??????, ??????????, ???????, ???????, ????????? ??????, ??????? ? ?????? ??????.
clearvisionfirst – Motivating content, shows that having a clear vision before acting produces better outcomes.
More Details: https://speech-language-therapy.com/media/articles/how-to-choose-the-best-online-casino-bonus-for-you.html
clarity fuels momentum – Focused effort transforms plans into continuous results.
measured action – Taking steps with intention produces outcomes that can be tracked and improved.
Experience Brainy https://askbrainy.com the free & open-source AI assistant. Get real-time web search, deep research, and voice message support directly on Telegram and the web. No subscriptions, just powerful answers.
?????? ???????? ????? ???????? ????? ??????? ? ????????? ?? ?????? ? ????????, ????????? ??????? ????, ???? ???????? ????? ? ???????, ????????? ?????? ?????. ???????? ?????????, ??????? ???????? ???? ? ??????.
start effectively guide – The guidance is easy to follow and motivates action without delay.
intentional results – Planning and acting with purpose guarantees measurable progress.
effective direction – Clear direction reduces uncertainty and increases the impact of actions.
progress through focus – Alignment of steps and intentions ensures effective and lasting progress.
strategic focus – Clear attention and commitment produce continuous results.
?????????? ??????? ?????? — ?????, ??????, ????????
https://play.talkdrove.cc.nf/@rolandowhitema?page=about
idea to execution – Following through on concepts produces fast and reliable results.
???????????? ?????? ? ??? ?? ????? kuhni-na-zakaz-2.ru .
????? ?? ????? ??? ???????? ? ?????? kuhni-na-zakaz-5ru .
????? ??? ????? ????? ??? ????? .
??????? ? ????? ?????? ????????? ???????? ?????????, ???????? ????, ??????? ? ?????????, ?????? ? ????????, ??????? ?????? ??????????, ???????? ?????? ? ??????????. ???????????????, ??????, ?? ?????.
??? ???????? ????? ? ??? kuhni-spb-17.ru .
?????? ????? ?? ????? ?? ????????????? kuhni-spb-18.ru .
clarity-driven movement – Insightful planning turns ideas into continuous forward action.
idea momentum – Moving ideas ahead consistently leads to tangible achievements.
focused effort – Concentrated attention drives consistent and measurable progress.
kraken onion kraken4 darknet
???????? ????? ??? ???????????? ???????? ???????????? ? ???????????????. ??????????? ??????????, ????? ??? ????, ?????? ? ???????, ??????? ???????? ??????, ???????????? ??????????? ? ????????. ?? ?????? ???????????? ???? ??? ?? ???????, ??? ????????? ? ????????. ?????????? ????????????? ???????? ????? ??????, ???????? ?????????? ? ?????????? ????????. ??? ???????? ???????????? ??????? ????????? ??? ?????? ? ???? ? ??????????
concentration counts – Practical examples of how focus leads to consistent progress.
outcomesthroughdirection – Motivating guidance, shows how deliberate direction ensures reliable results and effective progress.
?????? https://seoprofi.org/ ???????????????? ?? ?????????? ???????? ?????????? ??? Rutube ? VK ?????, ? ????? ?????????? ??????? ?? ???-????? ? ???????????? ?????????????? ???????????. ????????? ???????????? ????????? ????????? ?? ?????? 50-80%, ????????? ???????? ?? 1-3 ???? ? ?????????? ?????? ?? 1200 ?????? ?? 1000 ?????? ???????. ???????? ????????? ????????? ???????????? ????????, ????????? ?????? ?????? ?????????? ? ???????? ???????? ??????? ? ??? ??? ?????? ?????????? ??? ?????????????? ?????????.
focus and act – Concentrated thought with immediate action enhances productivity.
??????? ???????? ?? ?????? ?????? ??????
??????? ?????? ? ??????? ???????? ?? ?????? ?????? https://igroavtomaty.com — ??? ???? ? ????????? ? ???????????? ???????????. ??????? ??????????? ???? ?????????? ??????????? ???????????? ??????, ?????? ?????? ? ??????????? ???????? ????? ? ????? ?????. ?????? ????? ????? ??????? ??????????? ???????, ????????? ?????????? ?????? ? ?????????????? ????????? ? ?????????. ?????? ?????? — ??? ????????? ??? ? ???? ???????????? ??????-?????????, ??? ?? ????????, ??? ??????? ???????? ????????, ?? ??? ???????? ???????? ? ????? ????? ? ??? ??????? ???? ??????????.
???????????? ???? ?? ???????? ?????? ? ??????-??????
??????? ?? ???????????? ??????? ????????? ? ???????? ?????????? ?????? ??? ??????????? ???????? ??? ????? ??? ??????????? ???????????. ??????? ?? ??? — ??? ??????????????? ??????? ??????????? ? ????????. ? ??????? ?? ???????? ??????, ?? ??????-??????? ???????? ?????????????, ? ??? ?????? ???? ??? ????? ???? ?????????? ????????.
????? ????, ?????????? ??? ? ??????????? ??????????? ????? ????? ??????????? ?????? ????????? ??????? ?? ???????? ???????????. ??? ????????? ????????? ????????????? ????? ????????????? «??????????» ??????????, ???????????? ???????????? ? ????????????? ??????? ? ???????? ?????????? ? ?????????????? ??????????. ??? ???? ??????? ???? — ??? ??????? ????????? ??? ????? ? ?????????? ????????, ??????? ????????:
• ?????????????? ?????? ? ????????, ??????? ??????????? ??????????? ??? ????????? ????????.
• ????????? ?????????? ? ??????, ???????????? ????? ??????????? ???????.
• ?????????? ??????? ? ?????, ??? ????? ????????????? ? ??????? ???????? ?? ??????? ?????.
????? ????????, ??? ?????? ??????-???????? ????????? ??????? ???????? ??????? ???????? ? ????-??????, ????? ??????? ?? ??????????? ??? ????? ??? ???????????? ???????.
???????? ?????? ????????? ??????-?????? ??? ???? ?? ??????
???????????? ? ????????? — ???????????? ????? ?????? ????????, ??? ?? ?????????? ?????? ?????? ?? ??????? ???????? ?? ??????. ???? ? ???????????? ?????????? ????? ???????? ? ?????? ??????? ? ?????? ??????. ????? ????? ????????, ?????????? ????????? ????????? ????????? ???????? ????????.
?????? ?????, ?????????, ??? ?????? ???????? ??????????? ????????? ?? ????????????? ??????????, ?????? ??? Curacao eGaming, Malta Gaming Authority ??? ??????. ??????? ???????? ????????????, ??? ???????? ???????? ????????, ??? ???? ???????? ?????????? ???????? ?? ?????????, ? ???????????? ??????????????. ????? ????? ??????? ????????? ????????? ?? ??????????? ??????? ? ? ?????????, ??????? ???????? ?? ???????? ?????? ????????? ? ?????? ?????? ?????????.
?? ????? ????? ????? ??????? ? ?????????? ???????? ?????????? ?????????? ????????. ??????? ?????? ?????????? ????????? ????????? ??? ???????? ? ?????? ???????:
1. ?????????? ????? (Visa, Mastercard) — ????????? ? ?????? ???????????????? ?????.
2. ??????????? ???????? (?Money, Piastrix, FK Wallet, Telegram Wallet) — ???????????? ??????????? ? ??????? ???????? ??????????.
3. ???????????? (USDt, Tron, Ton, Bitcoin, Ethereum) — ??????????? ??????? ??? ???????????? ??????????????????.
4. ????????? ??????? ? ????????-??????? — ??? ??? ??????????? ?????????? ?????.
?? ??? ???????? ??? ?????? ?????? ???????? ????????
????? ???????? ???????? ???????, ??????? ????? ???????????? ? ????? ????????????. ?? ??? ???????? ???? ? ????? ?????????, ? ?? ?????????????? ?????? ???????? ?????? ?? ??? ??????? ????. ????????? ???????? ?????????? ??????? ??? ?????? ?????????? ?????.
???? ?? ??????? ??????????? — ??? RTP (Return to Player), ??? ??????? ???????? ??????. ??? ????????????? ????????? ??????????, ??????? ?????????????, ????? ????? ?? ???? ???????????? ? ??????? ????? ?? ?????????? ??????? ? ???????????? ???????????. ????????, ???? ? RTP 97% ????????? ????? ??????, ??? ??????? ? ??????????? 94%. ?????? ?????????? ?????? ???????? — ????????????? (??? ?????????). ??? ?????????? ???????? ??????:
• ???????????????? ????????: ????? ?????? ?????????? ??????????, ???????? ??? ???? ? ???????????? ??????? ? ????????? ??????? ??????.
• ????????????????? ????????: ?????????? ?????? ????? ???????? ? ???????? ??????, ??????????? ????? ??? ??????????? ???????.
• ????????????????? ??????? ????????: ??????? ????????? ????, ?? ????? ???? ????? ????????. ????? ????? ??????? ???????? ????????? ? ????????.
????? ????? ???????? ???????? ?? ???????????? ????? (?????????? ??????????: Novomatic, Igrosoft, NetEnt, Play’n GO) ? ??????? ????????????? ???????? ???????, ????? ??? ?????????? ????????, ????-???? ??? ??????? ? ???????????.
???????? ??????? ????????????? ???? ?? ??????
???? ? ??????-???????? ?? ???????? ?????? — ???, ? ?????? ???????, ???????????, ? ?? ?????? ?????????. ????? ???? ????? ????????? ???????? ? ??????????????, ?????????? ?????????????? ???????, ?? ??????????? ??????.
?????? ?????????????? ??? ???? ??????? ????? ??????? ?? ???? ??????? ?????? ? ?????? ??? ???????????????. ??????? ?? ????????? «??????????», ?????????? ?????? ? ??????? ?????? ??????? ??????????? — ??? ?????? ???? ? ??????? ???????. ????????????? ???? ??????? ??? ????? ?? ???????????, ? ????????? ??????? — ??? ???????? ?????. ??????????? ???????????? ?????? ?????????? ??????????? ??? ????????????: ??????????? ?????????? ?????? ?? ?????????? ?????, ??????????? ? ??????? ???? ? ????? ??????????????.
FAQ: ?????????? ??????? ?? ??????? ????????? ?? ??????
????? ???????? ???? ?????? ????? ??????????
?? ?????????? «????? ??????????» ?????????, ??? ??? ????????? ??????? ???????? ???????????? ??????????? ????????? ?????. ?????? ?? ?????? ???????? ????? ? ??????? ??????????? RTP (???? 96%) ? ?????????? ??????? ?????????????, ??? ???????????? ??????????? ???? ????? ?? ???????? ?????? ? ???????????? ???????????.
??? ???????? ???????????? ???? ?? ????????? ??????
???????????? ??????? ??????????? ?????? ?? ?????? ????????? ??????, ??????? ??????????????? ??????????. ????????? ????? ????? ????? ???????????? ???????, ???? ? ?????? ?, ???????, ????????? ??????????, ??????? ?????? ?????? ?????? ?? ???????.
??? ????? ??????? (???????) ???????
??? ???????, ??????? ??????? ????????? ????? ?????? ???????????? ?????????? ??? ????? ??????? ?????????? ???????. ????????, ???? ?? ???????? 1000 ?????? ? ????????? ?30, ??? ????? ??????? ?????? ?? ????? ????? 30 000 ??????, ?????? ??? ??????? ??????.
????? ?? ?????? ? ??????? ???????? ?? ?????? ? ?????????
????????? ??. ??? ??????????? ??????-?????? ????? ?????????? ?????? ?????? ??? ??????????? ????????? ?????????? ??? iOS ? Android, ???????? ?????? ? ????? ????? ?? ?????????.
??? ?????????? ????? ??????????
????? ??????? ?????? ?????????????? ?? ??? ?? ?????, ??????? ????????????? ??? ?????????? ?????. ????? ??????? ??????? ?????? ???????????? ?????? ???????? ??????????? ?????? ???????? (???????? ??????????), ????? ???? ???????? ?????????????. ????? ??????? ?? ??????: ??????????? ???????? — ?? 24 ?????, ?????????? ????? — 1-5 ?????????? ????.
advance with focus – Clear understanding allows actions to be purposeful and results-driven.
??????? https://nazenazeblog.com/ ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
????? ?? ????? ??? ??????? kuhni-na-zakaz-2.ru .
???????? ????? ?? ?????????????? ???????? ? ??? ???????? ????? ?? ?????????????? ???????? ? ??? .
??? ???????? ????? ? ??? ??? ???????? ????? ? ??? .
????? ?? ????? ????? ????????? ?? ????????????? kuhni-spb-17.ru .
momentum builder – Good way to spark action and avoid stagnation.
clarity in motion – Helps maintain focus and consistency in achieving goals.
???????????? ?????? ?? ????? ? ????? ?????????? kuhni-na-zakaz-3.ru .
????????????? ????? ????? ??????? ?? ????????????? ????????????? ??????: ?????? ??????? ? ??????????? ??? ?? ???????: ????????, ??????????????????????, ????????? ?????. ???????????????.
execution momentum – Keeps practical steps moving toward results.
growth through focus – Concentrated attention helps achieve meaningful and lasting results.
clarity hub – Keeps all actions visible and organized for easier execution.
results through focus – Keeping focus sharp ensures goals are met efficiently.
? ????????????????? ??? (??????????? ?????????? ???) ???????? ? ???? ????? ?????, ??? ???????????????? ????? ? ???????? ??????. ???????????????? ????????? ???????? ??????? ??????? ??? ?????????? ??????. ???????? ?????? – ??? ????????? ???? ???????????, ????????????? ???????? ?? ????????????. ?????? ????????????????? ??????? ?????????? ??? ????????? ??????????? ????????? ???????????. ??????????, ???????, ?????????? ? ????? – ??? ??? ????? ???????? ? ????????, ????? ??????????? ?????????? ???????????? ???????. ??????????? ?????? ? ?????????? ???????????? ?? ???????????? ??????? ??????? ??????????? ? ??????? ??????????? ?????????.
?????????????? ??????? ?? ????????? ?????? ?? ????????? – ??? ?????????? ????? ???????, ??????????? ? ?????????? ?????????, ???????????? ? ??????????? ?????? ?????? ????? ? ??????????? ???????????? ??????. ??????????? ?????? ? ????? ?????????? ????????? – ??? ??????? ?????? ???????????? ??? ?????????? ????????????????? ?????????? ? ????????? ??????? ?????. ??????? ?????? ?? ????????? ???????????? ?????????? ???????? ???????????, ?????????? ???????? ? ??????????? ?????????? ?????. ??????? ????????? ???????? ? ?????? ????????? ??????????? ??? ???????????? ???????????? ????? ??????????? ??????? ??????? ? ????????? ????????????? ???????????? ????????????. ????? ?? ??????????? ?????? ??????? ?????????, ????????? ????????????? ???????? ? ?????????????. ??????? ???????? – ??? ???????? ?????? ??? ?????????? ???????? ? ?????????? ????????????. ??? ???????? – ?????? ??? ?????????, ????????????????? ??????? ? ??????????? ??????? ???????? ? ????????? ?????????????? ?????? ? ?????.
action planner – Helps organize actions for measurable results efficiently.
???????????? ??????? ??????? 3D-?????? — ??? ????????? ?????????? ??? ???????????????? ? ????????????. ?? ???????????? ?????? ?? ???????????? ???????? ? ??????? ?????????. ???? ???????? ? ????????? ?????????? ??????????? 3D-????????, ??? ????????? ????????????? ???????, ??????????????? ??????????? ?????????. ??? ?????? ???????????? ???????????? ? ???????????? ???????, ??? ???????? ??? ??? ???????, ??? ? ??? ???????????? ?????. ??????? ???? ??????, ?? ????????? ????? ? ??????. ????????? ? ???? ??? ?????????? ???????, ? ?? ??????? ???, ????? ????????? ????????? ???????? http://www.bidanfiller.com/en/bbs/board.php?bo_table=free&wr_id=345208. ??? ?????? ???????????? ?????????? ? ????????????? ???????.
launch clarity – Helps initiate actions confidently with a structured approach.
FarbWood https://farbwood.by ???????, ?????????? ?????????????, ?????????? ? ???????? ???????????? ??????????????. ?????? ???? ?????? ?????????? ????? ?? ??????? ??????????? ???????? ???? ?????? ? ????? ????? ?? 9 ???. ????????? ????? ?????? ? ??????, ?? ??????????? ??????? ????????, ??????? ?????? ???????????? ???????????? ?????? ??????? ? ????????????? ??????????.
goal-oriented actions – Helps translate ideas into practical achievements quickly.
task clarity hub – Helps simplify execution by maintaining central organization.
????????????? ? ?????? https://colorprofi.ru ??? ?????????: ????????? ??????????, ?????? ????????, ????????? ??????????, ?????, ?????? ?????? ? ??????? ??????????. ?? ?????????? ? ???? ?? ??????, ????, ???????? ? ?????????. ??????????? ?????? ? ?????? ?? ???????.
?????????? ????????? https://soft-sng.ru ??? ??????????: ????, ???????, ?????????, ?????????, PDF, ??????, ?????? ????? ? ????, ??????? ??? ???????. ?????????? ? ??????????? ??????, ??????? ??????, ?????/?????? ? ???????. ?????? ?? Windows/macOS/Linux, ???????? ? ??????????.
clarity manager – Shows practical methods to manage operations with focus and efficiency.
forward momentum – Encourages persistent action that drives results.
https://inormal.ru/zhizn/kak-uvlech-malyshei-angliiskim-prakticheskie-podhody-dlya-domashnih-zanyatii
action trigger – Strong idea, it motivates people to take action instead of waiting.
momentumspark – Encourages generating momentum by sparking clear and intentional actions.
????? ????? ??? ???????? ????? – ??? ?????? ???????? ? ???????? ????????.
??????? ???? ? ?????? ??????: ???????? ?????? ? ????? | Skupka-Dronov https://skupka-dronov.ru/skupka/rossiya/prodat-dron-v-nizhnem-tagile-vygodnaya-skupka-i-obmen-skupka-dronov/
actioncompass – Emphasizes leveraging intelligence to navigate actions effectively.
alignment constructor – Keeps actions coordinated with overall objectives.
https://nodepositcasino.ru ?????? ? ????????????? ??????? – ??? ????????? ??????? ??? ???, ??? ????? ??????????? ???? ???? ? ???????? ?????, ?? ?????? ???????????? ????????. ??????, ????? ???, ??? ??????????????? ????? ????????????, ??????????? ??????? ??????? ? ??????? ??? ????????? ? ????????.
momentumshiftlab – Motivating guidance, explores methods to maintain momentum while adjusting direction strategically.
goal launch – Provides a clear path for moving toward objectives quickly.
task activator – Encourages action with a clear sense of direction.
taskaccelerator – Focused execution helps reach milestones faster and smarter
focus path – Shows a clear route for taking effective and purposeful steps.
operations strategist – Offers strategic insights to align operations with clear outcomes.
action enhancer – Helps make every step more effective and impactful.
Clarity Compass – Methods for guiding mental focus to achieve consistent success
Focus Route – Advice on creating organized attention flows for effective outcomes
sparktodrive – Highlights ways clarity sparks drive and momentum in execution.
?????? ????? ?? ????? ?? ????????????? kuhni-na-zakaz-2.ru .
Energy Hub – Channels motivation into practical actions that deliver results
growthwithframework – Useful advice, highlights that consistent growth comes from following a clear and structured plan.
??????? ?????? https://moskva-news.com ? ?????????? ???????: ????????, ?????????, ????????, ????????????, ?????????, ??? ? ??????. ??????????? ?????????, ??????????? ?????????, ??????????? ????????? ? ????. ??????? ?? ???? — ??????, ?????, ??? ???????.
?????? ? ????????????? https://strojdvor.ru ??????? ? ?????????? ????????: ?? ?????????? ?? ??????? ? ????????????. ????????? ??????????, ????????? ??????????, ???????, ?????? ????????? ? ??????? ??????. ???????? ??????? ??????? ? ??? ????????.
??????? ??????? https://lratvakan.com ???????: ?????? ?????????? ?? ?????? ?????, ?????? ?????????, ????????????? ????????, ????? ? ??????. ??????????? ??????????, ??????????? ????????? ? ???????? ?????? ??????? ??????? ???.
actionable vision – Clear forward-thinking strategies translated into action create impact.
Strategic Focus Hub – Highlights how aligned planning improves consistency
decisionpivotlab – Practical guidance, shows how shifting decisions experimentally drives better outcomes today.
??? ???????? ????? ? ??? ??? ???????? ????? ? ??? .
smart execution – Reinforces acting in ways that serve clear goals.
intellinavigator – Shows how applying directional intelligence keeps projects on track efficiently.
planning drive – Provides structure to keep actions organized and on track.
????? ?? ????? ??? ???????? ? ?????? kuhni-spb-18.ru .
vídeo pornográfico xxx com bunda grande
?????? ????? kuhni-spb-17.ru .
clarity compass – Helps navigate actions while staying aligned with goals.
priority launchpad – Focuses on initiating high-impact tasks for immediate results.
????? ??????? ??????????? ??????? ??? ????, ???? ? ?????????? ?? ???????? ?????? ???????? https://becompact.ru/ – ? ??? ????????? ??????? ?? ?????? ????? ? ??????? ????????? ?? ??????. ?????????? ??? ???????, ? ??? ?? ??????? ??? ?? ??????? ??? ?????????? ? ?????????????? ?????????? ?? ??????????? ?????? ? ??????????? ????????????.
clarity compass – Acts like a compass to guide tasks and priorities with clarity.
structured direction – Makes following the right steps simple and organized.
?????? ??? ????? ??? ?? ????????????? kuhni-na-zakaz-3.ru .
orchestration guide – Provides a framework to synchronize actions efficiently.
https://mixtum.online/ is a premium Bitcoin mixer that will provide you with an unrivaled level of anonymity. Learn more about all our advantages on our website and try out our new mixing mode with unique processing parameters. We offer a free trial and no registration required.
Focus Mapper – Steps to chart attention and track progress across tasks
claritylaunchhub – Highlights ways to launch projects efficiently by keeping focus clear from the start.
forwardignition – Very motivating, shows how igniting forward action drives momentum and meaningful results today
knittochka.ru
executionstructure – Very practical, shows how structured execution enhances clarity and consistent progress.
task engine – Keeps daily tasks moving efficiently toward completion.
plan bridge – Helps map out how ideas can become actionable plans.
taskvelocity – Accelerating tasks while staying focused improves outcomes
decisionpath – Highlights using a directional map to simplify decision-making processes.
implementation mapping – Helps move from ideas to action using mapped steps.
Aligned Growth Hub – Focuses on keeping actions connected to measurable goals
Attention Pathway – Tips for directing mental effort toward meaningful achievements
???????? ?????? https://vashesamodelkino.ru ??? ???? ? ????: ?????????? ???? ?? ?????? ???? — ?? ?????? ? ??????? ?? ???????? ????? ? ??????? ???????. ???????? ??????????, ??????? ???????? ? ???????, ??????? ??????? ???????? ? ???????? ?????.
action layout – Nicely arranged concept that supports better execution.
??????? K-POP https://www.iloveasia.su ?? ?????: ?????-??????, ????-???????, ???????, ????????, ???????? ? ???. ?????????? ??????????, ???????? ????????? ??????????, ???? ? ?????. ??????? ?? ???????? ????????? ? ???????? ????????? ?????? ????.
??? ? ??????? https://svoimi-rukamy.net ?????? ??????: ???????? ?????, ?????, ??????? ? ???????? ??? ???????? ? ????. ???????? ? ???????? ??????, ???????, ?????? ?????? ? ?????????? ?????????. ?????????, ???????? ? ??? ?????? ??????.
clarity map – Acts as a map to follow clear paths through tasks and goals.
keep progressing – Encourages continuous movement toward objectives.
practical action plan – Offers methods to stay on track and achieve measurable outcomes.
Attention Evolution – Methods for gradually improving focus for reliable outcomes
top free pornsites 2025 sex videos
projectclarity – Shows how structured clarity at the start ensures smooth project execution.
Task Momentum Hub – Helps maintain energy and efficiency across all tasks
????? ???????? ???? ????? ?????? – ??? ????????????? ???????, ??????? ???????? ??? ??????? ??????????? ???????, ????????? ?????????? ? ????? ???????????.
actionengine – Motivating guidance, demonstrates how directional systems act as engines for steady advancement.
clarity framework – Builds understanding and direction for daily tasks.
????????????? ??????? ??????? ???? ????????????? ??????? ??????? ???? .
clarity execution – Guides effective action by keeping tasks clear and focused.
focused execution – Aligning steps with strategy improves consistency and results.
goalnavigator – Demonstrates using directional tools to align actions with objectives.
?????????? ?????????? ???????????? ?????? — ????????? ????????
https://reexhk.com/author/neilnorcross07/
????????????? ???? ?????? ?? ?2 gidroizolyacziya-czena4.ru .
??????????? ????????????? ?????? ? ????????????? ??????? ?? ??? ?????????: ?????? ??? ???????-???????????? ?????????????. ??????????? ??????????, ????????? ??????? ?????? ?? ????????? ? ????????? ???.
????????????? ??????? ?????? ????????????? ??????? ?????? .
execution mechanism – Explains how clarity ensures tasks are completed effectively.
?????????? ???????? ? ??????? ?????????? ???????? ? ??????? .
????? ????? ??? kuhni-na-zakaz-2.ru .
task pathways – Provides guidance on organizing tasks into actionable pathways.
purpose-driven action – Focuses on deliberate steps that create real outcomes.
Growth Alignment Hub – Acts as a central place to coordinate growth efforts and keep teams aligned
goal pathfinder – Guides toward the most efficient way to reach goals.
Task Route – Techniques for aligning focus with key priorities
claritynavigator – Provides guidance on navigating tasks effectively using a structured clarity system.
workflowignition – Activating attention helps teams perform at their best
Progress Engine – Demonstrates how sustained action moves projects toward results
clarity framework – Encourages cleaner decisions and more intentional movement.
actionmind – Practical tips, emphasizes directing thought processes to achieve clear and measurable results.
priority hub – Helps keep important tasks aligned and visible.
focus navigator – Directs attention and effort smoothly to priority tasks.
More Details: https://joker778.org/buy-tiktok-ads-accounts-what-are-yahoo-ad-possessions-how-to-use-all-of-them-with-instances/
Productivity Engineer – Ways to engineer attention for better task management
directioncompass – Shows how a clear path guides decisions and actions effectively.
growth optimization view – A thoughtful explanation focused on improving growth efforts
initiative momentum – Demonstrates how clarity powers the start and continuation of important initiatives.
creative idea builder – Helps structure ideas clearly and convert them into practical actions quickly
????? ?? ????? ????? ????????? ?? ????????????? kuhni-spb-17.ru .
????? ?? ????? ? ??? ????? ?? ????? ? ??? .
????? ??? ????? ??? ????? ??? ????? ??? .
progress navigator – Guides actions to maintain momentum and clarity in execution.
idea prioritization focus – Helps identify key ideas and execute them effectively
task framework – Offers a practical method for managing and completing tasks.
Mind Navigator – Tips for keeping focus on a productive course every day
clarityhub – Provides a hub for integrating processes with clear guidance for better outcomes.
clarity pathway – Provides a transparent view of the steps to take next.
task navigator – Channels effort for more efficient task completion.
purposecompass – Engaging advice, highlights applying directional vision to maintain focus and productivity.
forwardmovementlab – Useful guidance, experiments with strategies to improve movement and achieve measurable progress effectively
?????? ????? ?????? ????? .
Strategic Growth Builder – Demonstrates assembling growth initiatives with clarity and intent
task focus – Keeps important tasks prioritized and executed effectively.
focuspathfinder – Emphasizes focused decision-making to maintain direction and achieve outcomes.
methodical progress – Structured and precise steps drive consistent achievement.
trans porn
clarity motion – Highlights how clear thinking sustains continuous action and smooth progress.
right direction – Keeps actions aligned when options feel unclear.
????? ?????????? ????????? ????????? ???????? ??????? ????? ???????????? ??????? K-beauty. ???? ??? ???? ????? ????, ??????? ? ???? ??????. ??????? ????????? ????????, ???????? ????, ????? ? ??????????? ???????? ?? ??????.
growth workflow insight – A practical breakdown of growth processes for teams
idea builder guide – Provides a systematic approach to turn concepts into actionable steps efficiently
clarity lanes – Shows how organizing lanes of action ensures smoother progress.
workflowengine – Strategic focus activation improves team workflow and results
executeideasnow – Inspiring guidance, demonstrates that putting ideas into action is essential for measurable success.
guided action – Provides practical direction to make decisions with certainty.
Focus Director – Guidance on maintaining attention on purposeful objectives
focus navigator – Directs attention and steps toward optimal outcomes.
idea action focus – Provides methods to keep ideas prioritized and executed successfully
actiontracker – Shows practical ways to track actions and stay aligned with goals.
?????? ? ????????????? ??????? ?????? ?????? – ??? ???????????? ????? ????????? ??????-?????????. ??? ????? ???? ??? ??????????????, ??? ? ???????????, ? ???????????? ??? ?????, ??? ? ?????????? ???????. ??????? – ????? ????????? ?? ???????????? ? ?? ???????? ?? ????????????? ????.
project planner – Guides tasks and actions to ensure smooth project execution.
Daily Summary: https://documentaryheaven.com/real-peaky-blinders/
workstreamfocus – Proper workflow management ensures projects finish on time
????? ????????? ????????? ????? ????????? ???? AniMatrix – ??? ?????? ??????????????????, ????????? ? ?????? ?????-?????.
Task Path Hub – Offers clear pathways to complete tasks effectively and quickly
Idea Architect – Techniques to create clear paths for innovative thinking
task forward – Keeps tasks progressing smoothly toward desired outcomes.
roadmapplanner – Provides a roadmap approach to organize actions and maintain direction.
focus lab – Explores techniques to channel clarity into consistent and productive execution.
Growth Execution Hub – Shows how structured channels improve execution quality
?????? ??????? ?????? ??????? .
idea development hub – Provides guidance to transform creative concepts into practical solutions
growth momentum framework – A thoughtful explanation of how momentum supports stable growth
progresshub – Highlights a hub approach to streamline routes and maintain steady progress.
alignment companion – Ensures all actions are synchronized with objectives.
building momentum – Encourages steady progress through structured actions.
step-by-step map – Visualizes actions so each step is clear and achievable.
Momentum Builder – Advice for sustaining focus while driving consistent progress
actiontrajectory – Highlights tracking a trajectory to maintain steady progress toward long-term objectives.
taskartisan – Organizing work precisely ensures consistent, focused results
????????????? ???? ?? ????? ????????????? ???? ?? ????? .
Read more on the website: https://ezeller.com/buy-aged-facebook-accounts-on-line-ads-to-own-accounting-firms-were-cpa-sale-professionals/
???????????? ????????????? ???? ??????? ???????????? ????????????? ???? ??????? .
momentum starter – Motivates initiating actions promptly for faster results.
creative idea forward – Helps move concepts ahead efficiently to achieve measurable outcomes
kraken darknet market ?????? ??? 1pw
???????? ????? ??? ???????????? ???????? ???????????? ? ???????????????. ??????????? ??????????, ????? ??? ????, ?????? ? ???????, ??????? ???????? ??????, ???????????? ??????????? ? ????????. ?? ?????? ???????????? ???? ??? ?? ???????, ??? ????????? ? ????????. ?????????? ????????????? ???????? ????? ??????, ???????? ?????????? ? ?????????? ????????. ??? ???????? ???????????? ??????? ????????? ??? ?????? ? ???? ? ??????????
Clarity Planner – Provides a structured approach for clear and actionable outcomes
?????????? ????????????? ???? ?? ?????? ?2 gidroizolyacziya-czena5.ru .
focus navigator – Directs attention and actions toward meaningful priorities.
focus movement – Illustrates how focused clarity generates meaningful and consistent motion.
focusflowplanning – Highlights planning methods that create smooth and productive action flows.
action in sync – When actions are aligned, creativity and results flow naturally.
taskalignment – Aligning focus with goals ensures projects move forward smoothly
clarity in action – Helps ensure ideas are clearly defined for consistent results
task compass – Organizes daily work to ensure smooth progress.
?????????? ??? ????? ?????
movement for growth – Sounds like a collaborative effort centered on steady business growth
Mind Ignition – Strategies to fire up concentration and achieve goals quickly
Growth Control System – Explains building systems that keep growth organized
claritypath – Emphasizes mapping a vector to ensure actions stay purposeful and productive.
Mind Clarity Hub – Techniques for staying clear and intentional in task execution
productivitylane – Organized approaches make achieving goals easier
task flow map – Visualizes how steps connect to keep progress smooth.
Progress Navigator – Guides projects along a path of steady advancement
execution structure – Supports consistent implementation by structuring tasks effectively.
creative idea launchpad – Shows practical ways to accelerate ideas into actionable steps
Fresh news on Page: https://euromarches.org/wp-content/pgs/what-is-an-rng-and-how-does-it-work-in-slots.html
action cycle – Smart perspective that explains how repeated actions lead to steady improvement.
decision initiator – Supports making choices and taking action promptly.
clarity guide – Offers guidance to make well-informed decisions consistently.
actionlab – Demonstrates experimental approaches to enhance action-oriented planning.
idea-to-action conversion – Shows how transforming ideas into actions accelerates real progress
workflowsequencehub – Demonstrates structuring workflows in a hub to maintain steady progress.
??????????? ??????? ? ???????? ???? ?????????? ????????? ????????? ?????????? ??????? ???????????????? ???????? ?????? ?????????. ?????????????? ?????? ????????????? ????????? ? ???????????? ????????????? ???????? ? ??????????? ??????? ???????, ?????????? ??????????? ?? ????? ? ??????????? ??????????? ???????. ?? ????????? https://velakast.online/ ??????? ?????? ? ??????? ??????????, ?????????? ? ?????????????????, ? ????? ???????? ?????? ?????????, ????????? ???? ???????. ????? ???????, ??? ????? ??????????????? ??????? ??????? ??????????????? ???????????? ? ????????????????? ??????-??????????????, ??????? ???????? ??????????? ????? ??????? ? ?????? ???????? ?????? ? ????????? ??????.
goalpath – A clear path helps teams reach objectives smoothly
clarityflow – Shows how clear workflow design supports smooth project execution.
Design Director – Practical advice for guiding forward-thinking plans to successful outcomes
growth navigation path – Offers insight into progressing through growth thoughtfully
action grid – Organizes tasks to make execution clear and efficient.
????? ???????? ????????? ??????? ????????? xn--rdacteurmmoire-bkbi.com ?????????? ???????????????? ?????? ?? ????????? ????????????? ?????: ???????? (TFE), ???????????? ???????????, ?????????? ??? ? ???????? VAE ?? 18 ???? ?? ????????. ??????? ????????????????? ?????????? ??????????? ?????????????? ?????? ??? ????????, ?????????? ?????? ? ???????????? ????????? ????????? ? ??????????? ????????. ?????? ???????? ? ?????????? ???????????? — ?? ???????? ?? ?????????????, ????????? ?????? ????? ?????????? ?? 24 ????? ?? ???? ? ???????????? ????????????? ? ?????????????? ??????????.
Action Strategy Hub – Focuses on turning ideas into coordinated, forward-focused actions
goal trajectory – Shows the direction to ensure outcomes align with objectives.
Strategic Direction Hub – Emphasizes aligning actions with a clear growth course
focusnavigator – Centralized focus alignment leads to clearer actions and better results
priority lane – Focuses on high-impact tasks to maximize progress.
idea strategy mapper – Shows how mapping ideas supports strategic implementation and outcomes
focus guide – Offers insights for keeping actions aligned with clarity and purpose.
progressengine – Very practical, shows how directional methods maintain steady progress over time.
innovation-to-action converter – Helps transform creative ideas into tangible outcomes effectively
Mind Mapper – Strategies to visualize attention and streamline decision-making
????????????? ?????? ? ?????? ? ??
deployment guide – Provides direction for executing actions effectively.
strategicshift – Provides tips for shifting strategies while keeping clarity at the core of execution.
taskpath – Structured steps make completing tasks more efficient and predictable
intentflow – Shows how directing intentions leads to focused actions and outcomes.
ShowStaff https://showstaff.ru/ – ?????? ????????? ? ??????? ????! ???????? ????, ??? ?? ??????? ????, ?????????? ?????????, ?????????? ?? ?????????? ? ?????????? ?????. ?????? ?????????? ? ???????????. ?? ?????? ??????? ????? ??? ??????????? ? ??????, ??? ? ? ????????? ?? ????? ????! ?????????? ???????, ? ?? ??????? ??? ???? ???? ?? ??????? ????????!
https://progorod36.ru/internet-magazin-gazonov-sostavil-svoy-reyting-samyh-populyarnyh-gazonnyh-semyan-v-etom-sezone
Strategy Hub – Combines planning and action into a coherent workflow for success
growth insight hub – Brings together insights that simplify growth planning
????????????? ??????? ??? ???? gidroizolyacziya-podvala-iznutri-czena4.ru .
Momentum Hub – Explains how maintaining momentum contributes to faster advancement
???????? ??????? ??? ???, ??? ????????? ? ???????????
Feel free to visit my web blog :: https://t.me/s/cheburnet_bot_vpn
????? ?????????? ??????? ????????? ????????? ??????? ????? ???????????? ??????? K-beauty. ???? ??? ???? ????? ????, ??????? ? ???? ??????. ??????? ????????? ????????, ???????? ????, ????? ? ??????????? ???????? ?? ??????.
concept mapping tool – Provides practical steps to structure ideas for efficient execution
Engineered Growth Path – Shows how structured pathways guide steady results
claritypivot – Practical guidance, shows how a pivot in direction can improve clarity and execution today.
claritydrivesfocus – Engaging guidance, highlights how clear thinking over complexity leads to better decision-making.
creative execution elevation – Provides guidance to elevate ideas while ensuring practical results
????????????? ???? ?????? gidroizolyacziya-czena5.ru .
??????? ? ??????? ??????? ? ??????? .
directionarchitecture – Designing focus structures guides projects toward predictable outcomes
practical testing lab – Focuses on experimenting with real-world action scenarios.
Action Flow Activator – Helps turn strategies into consistent progress and tangible results
growth optimizer guide – Shares smart ideas for refining growth efforts with precision
????????????? ??????? ?????? ????????????? ??????? ?????? .
Schwarzes schwules Porno-Sexvideo
???????? «??????????» — ?????????? ???????????? ???????? ???? ? ?????????????, ?????????? ????? ???? ???????????. ??????????? ???????????? ??????????? ????????????: ?? ?????????? ?? ????????? ???????????? ???????????, ? ??? ????? SMT ? ?????? ??????, ?????? ??? ?? ????????????? ???????. ????????? ?? https://www.techno-svyaz.ru/ ??????????? ????????????, ????????????? ???????????? ?????????? ?? ??????? ??????? ? ????????????????? ???????? ??????????? ??????????? ????? ???????????? ??? ??????? ???????? ????????? ??? ????? ??????? ???????.
Attention Engine – Steps to power focus and maintain productive routines
structured idea momentum – Offers practical steps to maintain ongoing momentum in projects
innovation engineering – Offers practical ways to design and execute ideas effectively
???????? Noblelift Equipment JSC Ltd. ??????????????? ???? ??? ??????? ????? ?? ???????????? ????????? ??????? ? ?????? ????????? ????? ???????????? ??? ????????????? ?????. ?????????? ????????????????? https://nobleliftrussia.ru ????????? ??????? ??????????? ???????????, ??????????, ??????? ? ????????? ??????? ? ??????????? ????????? ?? 36 ???????. ????????? ??????????????? ?? ?????????? EAC, CE ? ISO 9001, ??????? ??????????????? ????? ??? ? 100 ??????? ????, ??? ???????????? ?????????? ???????? ???????.
growth framework playbook – Action-oriented content, outlines repeatable growth processes
??????????? ?????????? ??????????? ???????????? ???????? ???????? ?? ???? ??????. ??????????? ??????? ?????, ?????, ?????? ? ??????????? ???????????, ???????? ???????????? ? ?????????? ? ????????? ???????????? http://maxes.co.kr/bbs/board.php?bo_table=free&wr_id=2576625
growth improvement focus – Highlights daily effort as the key to better results
????? ????????? ??? ??????? ??????, ????????????? ? ???????? ???????? ???? https://xn--80abutqu5e.xn--p1ai/ – ???????????? ? ????? ???????????? ?????????, ? ??????? ?? ??????? ??? ??????????? ??? ??? ????????? ? ???????? ? ??????? ????????? ?????? ??????? ? ????? ???????. ???????? ? ??????????? ? ???????????? ??????. ????????? ?? ?????.
careful execution – Focuses on deliberate steps to increase effectiveness.
idea implementation hub – Guides on structuring and executing concepts for measurable results
“`
concept motion planner – Helps organize ideas to keep them progressing efficiently
“`
Focus Stream – Guidance for channeling your energy into meaningful tasks
idea guidepost – A simple description of pointing thoughts toward meaningful results.
https://github.com/logonx/Windows-App
Attention Momentum – Advice for keeping energy and focus aligned with goals
growth activation path – Practical overview, shows how starting now leads to measurable change
https://enran.ua/
?????????? ??????????? ??????? — ??? ?? ?????? ?????? ??????????, ?? ? ?????? ??????? ?????????????? ??????, ??????????? ?????? ??????????? ? ????????. ??????????? ?????????? ????????? ????????? ???????????, ?????????? ??????????, ???????? ? ????????????? ??? ???????? ?????????. ?????????? ???????? ???????????????? ?? ???????????? ? ??????? ????????????? ??????? ????????? ????? — ?? ????????????? ?????????????? ?? ?????????? ???????????-?????? ? ??????????? ?????????. ?? ????? https://xn--80aacmaomvzu5fyb2c.xn--p1ai/ ???????????? ???????? ?????????? ? ?????????? ???????????????? ? ?????? ?? 900 ?????? ?? ?????????? ????. ?????? ???????, ???????? ?????????? ??????????? ???????????????: ?????????? ?????? ? ???????????, ?????? ??? ??????????? ? ?????????????? ?????? ? ????? ????, ??????????? ?????? ???? ????? ??? ???? ? ?????? ? ???????.
“`
growth route planner – Offers practical steps to select the right growth route efficiently
“`
????? ????????? ??????? ????????-??????? eicom.ru ?????????? ???????????????? ???????? ??????????? ??????????? ? ???????????? ? ?????????? ?????????????: ????????????, ?????????, ??????????, ???????, ??????????????, ??????????????? ? ??????? ??????????. ??????? ????? 10 000 ???????, ????????? ???????, ??????? ???????? ? ????????????????? ???????????? ???????????? ???????? ?????????????? ??? ?????????, ???????????????? ??????????? ? ??????????? ???????????.
creative flow engine – Focuses on maintaining consistent momentum in executing creative ideas
structured workflow lab – Focuses on organizing and experimenting with steps for steady idea advancement
>progress-focused path – A structured approach for keeping intentions moving steadily forward.
planning lens – A helpful view on shaping ideas into workable strategies.
planned momentum system – A structured approach for guiding actions toward continuous progress.
?????? ??????????? ????????? ?????? ??????????? ????????? .
action vector momentum – Demonstrates how focused direction sustains productive forward motion.
architecture of progress – Highlights practical ways to design workflows that maintain steady forward momentum.
????? ???????????? ??????? ???????? ?????? kazlenta.kz ???? ???????? ?????????? ??????????? ?????????? ??? ????, ??? ?????? ?? ????????? ? ?????????? ? ???? ????? ??????? ?????? ??????? ????????, ?????????, ??????, ???????? ? ???????????? ? ??????? ?????????? ?? ????????. ??????? ??????? ????????? ?????????? ???????, ?????? ? ?????????? ? ???????? ??????, ?????????? ????????????? ??????????? ?????????? 24/7. ????????? ????? ???????? ???????????, ????????????? ???????? ?? ?????? ??????? ? ?????????? ???????????? ?? ?????? ????.
process-driven progress – Offers practical guidance for maintaining steady advancement with structure.
alignment structure – Demonstrates methods to structure actions to keep all efforts aligned.
Mind Framework – Strategies to build mental clarity and task efficiency
Experience Brainy https://askbrainy.com the free & open-source AI assistant. Get real-time web search, deep research, and voice message support directly on Telegram and the web. No subscriptions, just powerful answers.
growthlogic – Engaging content, shows how logical strategies enhance growth and lead to consistent, efficient outcomes
?????? – ?????? ????’?????? https://hotgoods.com.ua
growth pathway plan – Makes complex growth targets easier to achieve by dividing them
????? ????????? ??? ????????? ????? https://gortransauto.ru
idea development path – Offers clear guidance to implement and track creative ideas effectively
productive momentum design – A practical way to convert plans into measurable results.
focus framework – A practical way to explain narrowing ideas into defined paths.
>intentional action path – A helpful strategy to transform intentions into tangible results.
Decision Compass – Methods for maintaining clarity while making key choices
idea orchestration guide – Provides strategies to coordinate ideas effectively and achieve results smoothly
?????? ????????????? ??????? gidroizolyacziya-czena4.ru .
????????????? ???????? ???? gidroizolyacziya-czena5.ru .
mapnavigator – Guides keeping strategy initiatives clearly visualized and on track
strategic momentum vector – Offers structured approaches to align tasks and maximize results.
forwardalignment – Shows how aligning vision with operational steps drives measurable outcomes
????????????? ?????? ?????? ?????????? ????????????? – ????????? ??????? ??? ????????? ? ???????? ?????????, ????????? ????????????? ???????????? ? ??????????? ???????????? ?????????.
progress design framework – Highlights methods for designing workflows that ensure continuous forward momentum.
asian sports bookmakers 1cupis: ??????????? ??????????? ? ??????????? ???? ??????????? ????
pathengine – Shows structuring clear pathways to guide successful projects
implementationhub – Highlights coordinating efforts to turn plans into tangible achievements
claritydrivesmomentum – Motivating guidance, highlights that clear understanding and focus generate sustainable and measurable progress.
structured progress – Highlights ways to organize efforts to maximize consistent achievement.
momentum structure – Demonstrates practical ways to build a structure that supports ongoing progress.
????????????? ???? ????????????? ???? .
momentum execution designer – A structured approach for translating strategy into actionable results.
pipeline growth framework – Offers a framework to design and manage an effective growth pipeline
thinking engine – A supportive process that prepares concepts for smooth rollout.
purpose path vector – A straightforward way to move intentions into actionable steps.
innovation workflow path – Helps structure concepts into a defined path for success
actionmap – Demonstrates mapping steps to convert strategy into tangible results
efficient momentum works – Demonstrates strategies to make efforts count toward measurable goals.
strategynavigator – Highlights steering projects by aligning vision with measurable steps
Productivity Pilot – Step-by-step ways to channel attention toward high-impact results
goal achievement blueprint – Demonstrates ways to create clear frameworks for consistent progress.
visionpathway – Emphasizes guiding steps strategically to achieve outcomes efficiently
progress booster – Highlights ways to ignite momentum for faster and more consistent achievements.
????? cs go ???? ???????? ?????? ??
directional trajectory – Offers strategies to keep actions focused on achieving results.
????? ???? ??????????? ????????? ??????? Terapiazvu.com ?????????? ???????? ?????-????????????? ??????? ?????????? ??????? ?????? ?????? ?????? ? ??????????? ??????? ??????????-???????????? ???????. ???????????????? ??????? ???????? ??????????????? ???????? ??????? ?????? ? ??????? ??????, ???????? ????????? ?????????????? ?????????? ???? ???????? ?? ?????????? ? ???????????? ?????????? ???????? ?? ??????. ?????? ? ??????? ?????? ????????????? ????????? ??????????, ??????????? ?????????????? ????????? ???????? ? ???????????? ?????????? ?? ??????????????? ?????????.
Attention Planner Hub – Strategies for tracking focus and achieving key objectives
energy momentum driver – A clear method to transform intention into continuous advancement.
progress-focused thinking – A useful approach that keeps ideas moving in the right direction.
momentum roadmap – A useful framework that prevents stagnation and keeps progress going.
builderhub – Highlights central oversight to turn strategic plans into actionable results
architect of motion – Demonstrates approaches for designing action and achieving measurable results.
https://sykaaa-casino-website.fun
goaloperations – Guides keeping operations focused on achieving objectives efficiently
execution booster – Offers methods to trigger forward steps and achieve measurable outcomes.
forward spark – Demonstrates ways to ignite momentum and ensure productive outcomes consistently.
focusedjourney – Highlights staying on course to reach impactful milestones
driving momentum engine – A structured approach to ensure continuous and reliable outcomes.
3snet info canadian gaming summit: ?????? ?????????? ?????????? ????? ?? Canadian Gaming Summit
Focus Director – Advice on steering mental energy toward meaningful work
planning route – A focused approach to moving ideas forward with confidence.
catalystpath – Guides defining clear pathways to activate vision into results
progress design system – A structured approach to ensure ideas grow steadily.
productive motion strategy – Shows strategies for sustaining energy and focused forward movement.
plannavigator – Guides mapping steps to achieve goals efficiently
strategy circuit – Highlights ways to connect strategic steps for efficient progress.
progress catalyst – Practical guidance on sparking progress deliberately to achieve focused and tangible results.
executionedge – Focuses on giving strategies the edge to be executed effectively
momentum results guide – A clear system for achieving consistent and impactful outcomes.
https://github.com/ciscosdk/Cisco-AnyConnect
??? IT-?????? https://nashkomp.ru/ – ??? ????????? ? ???? ??????? ??????????. ????????? ????????? ?????????? ??????? ?? ????? ?????????, ?????? ??????? ?????? ? ????? ???????? ????????. ?? ????? ?? ??????? ????????? ????? ???????????? ???????????, ???????????? ??????????? ?? ???????????????? ? ?????? ?? ?????????????????. ?? ????? ?????? ? ???????: ?? ??????????? ?????????? ?? ?????? ???????? ??. ???? ???? — ??????? ?????????? ?????????? ??? ?????????????? ? ???????????. ?????? ? ????? ???????? ??????? ?????? ? ????!
focusdirection – Shows how focused direction ensures goals are achieved efficiently
idea path selector – A useful approach for choosing the right direction for ideas.
motion results system – Provides practical methods for sustaining motion and achieving clear outcomes.
motion toolkit – A simple yet effective set of strategies for continuous progress.
actionplannerhub – Highlights managing strategy actions for consistent results
“`
momentum direction – Demonstrates how clear direction ensures ongoing progress and focus.
“`
structured logic – Offers techniques for maintaining focus and measurable progress through reasoning.
momentum direction tips – Highlights methods for aligning energy with tasks successfully.
executionengine – Emphasizes practical execution to ensure plans succeed
executionengine – Guides putting strategy into motion for consistent results
action roadmap – Provides practical steps that guide progress effectively
readable guidance – A clear and friendly approach that’s easy to follow today
clearvisionaction – Useful content, shows that having a clear vision directs tasks toward successful outcomes.
“`txt
idea roadmap – Shows how planning ideas systematically leads to success
“`
“`txt
focused growth – Helps prioritize tasks and achieve steady improvement
“`
“`txt
achievement map – Encourages mapping progress for measurable and consistent results
“`
initiativehub – Guides structuring initiatives to align with strategic vision efficiently
??????-????????? https://rosseriaall.net/ ?????????? ?????????? ???????? ?????????? ???????? ? ??????? ???????? ??? ???????????. ???? ???????? ????????????????? ?????, ??????????? ?????????????, ????????, ??????? ????????, ?????????? ? ?????????? ???????, ?????????????? ? ???????? ??????? ? ??????? ?????????? ?? ?????????? ? ???????? ???????. ???????????? ?????????? ??????? ???????? ??????? ? ?????? ???????? ???????? ????. ?????????? ?????????? ???????? ? ??????????? ????????? ????????? ?????? ????? ???????????? ?????? ? ?????? ???????? ? ????? ?????.
“`txt
focusfuelhub – Insightful guidance, helps channel attention and complete tasks efficiently
“`
idea action flow – A helpful perspective on converting plans into movement.
step guidance navigator – Demonstrates approaches to maintain clarity and achieve forward results.
momentum routing plan – A structured approach to turn momentum into tangible progress.
momentumhub – Encourages maintaining energy in strategic efforts for measurable outcomes
intentional driver – Demonstrates ways to purposefully guide progress for steady and impactful outcomes.
momentum efficiency lab – Offers guidance for testing ways to optimize workflow and results.
progress flow lab – Offers strategies to maintain momentum and move actions efficiently.
Looking for a casino? elonbet casino: slots, live casino, bonus offers, and tournaments. We cover the rules, wagering requirements, withdrawals, and account security. Please review the terms and conditions before playing.
actionalignment – Encourages making sure all efforts contribute to intended goals
action blueprint – Gives a structured path that ensures results are achievable
“`txt
actionable progress – Shows ways to convert planning into consistent daily results
“`
“`txt
brainstorm to action – Provides a framework to apply creative thinking effectively
“`
goalengine – Demonstrates turning vision into measurable achievements through focused actions
“`txt
roadmap tracker – Shows how to structure progress and stay on track consistently
“`
triggered action guide – Demonstrates ways to initiate steps that sustain momentum and forward movement.
impact creation flow – A smooth process that connects ideas with real-world effects.
sykaaa casino ???? ???? Sykaaa: ?????? ?????????? ? ??????, ??????? ????????, ??????? ? ???????.
clean structure – Information flows nicely and is very easy to understand
initiativevector – Shows how vector-focused planning keeps projects aligned and productive
planned progress – Highlights strategies for systematically organizing steps to reach objectives.
productive momentum guide – A practical method for ensuring energy is used efficiently.
momentum focus planner – Practical strategies to keep efforts consistent and results measurable.
motion strategist – Offers tips for planning forward motion to achieve outcomes effectively.
?????? ?????? ? ???????? AquaStop. ?????? ?? ????????. ?? 6000 ??.?????? ??????????????? (?????????) ???????? ????? ??? ????? ????? ?? ??????? ?? ????????? ???????? ?????????? (?????????), ???????? ???????? ??????????????? ?????? ? ???????? ??????? ????????? ???? ? ??????? ????. ??????????? ???????????? ??? ?????????? ?????? ????? ??????.????????????? ?????? ?? ????? ??????
“`txt
clarityguide – Very motivating, promotes clear thinking and effective execution
“`
alignmentengine – Streamlines strategy execution while keeping priorities clear and actionable
planlauncher – Highlights using strategy execution to accelerate progress efficiently
“`txt
idea to execution – Encourages converting thoughts into results consistently
“`
visionhub – Highlights organizing tasks and resources for consistent execution of vision
“`txt
momentum path – Encourages structured actions that maintain ongoing progress
“`
turn vision into action – Helps take clear steps from conceptual goals to real-world execution
“`txt
results engine – Shows simple and effective ways to make progress toward your objectives
“`
next step activation – Demonstrates ways to trigger progress consistently toward desired outcomes.
idea influence system – A practical method for ensuring ideas attract attention and support.
forward momentum foundry – A clear approach for molding energy into tangible, actionable results.
flow management – Offers techniques to sustain a steady workflow and maintain effective execution.
tacticworkflow – Highlights structuring tactical steps for smooth and efficient execution
?????? ?????? ???? kraken casino ????: ??????? ?????????, ??????? ????? ??? ? ?????????????? ????????? – ???, ??? ????? ??? ?????????? ????. ?????? ?????? ???????: ?????????? ???? ????????????? ?????? ? ??????? ????? ? ????? ????? ? ? ????? ?????. ??????? ?? ???????????????? ?? ???? ? ??????. ?????? ?????? – ??? ????? ??? ????????? ?????! ?????????? ? ????????, ????????? ?????? ? ??????? ???? ????????? ??????. ??????????????? ????? ?????? ? ??????? ?????? ???????????? ??????????!
“`
energy control framework – A structured guide for making decisions while maintaining progress.
“`
navigation guide – Practical tips for steering progress effectively toward clear outcomes.
outcomebuilder – Shows how structured strategy development leads to measurable results
?????? ????? ????? Haier. ????????????????? ?????????, ?????? ???????, ?????????? Err1, Err7.?????? ?????????? ????? Midea ?????? ????? ? ????????. ??????????? ?????? ?????????? ?????: ?????? ?????, ?????? ?????????. ?? ??????? ?? ??????? ??????, ?? ???????? ?????? ????????????. ?????? ?????????? ????? ????
“`txt
momentumclarity – Great insights, shows the link between clarity of direction and sustainable momentum
“`
?????????????????? ??????? https://tvoyprud.ru/ ?????????? ??????????? ??????? ??? ???????????? ????????????? ????????: ??????????????? ? ??? ??????, ??????? ??????????? ?????, ?????? ??? ???????? ? ????????? ??????? ??????? OASE, Jebao, Messner, ??????? ?????????? ? ???????. ????????????????? ??????????? ?????????, ??????? ????? ??????? ? ????????????? ??? ????????? ???????? ??????????? ??????????? ??????? ?????? ?????? ?????? ?????????.
alignmentframework – Shows ensuring all actions align with vision through structured planning
“`txt
productivity flow – Offers insights to keep work organized and efficient
“`
focused direction – The guidance here improves how I structure my project plans
“`txt
momentum focus – Helps prioritize actions to keep projects advancing effectively
“`
action roadmap – Provides a clear path for executing plans successfully
????????????? ??????? ?????????? gidroizolyacziya-podvala-samara2.ru .
????????? ???????????? ????????????? inekczionnaya-gidroizolyacziya4.ru .
?????????????? ???????????? ????????????? inekczionnaya-gidroizolyacziya5.ru .
??????? ????? ?? ????? ??????? ????? ?? ????? .
progress activator guide – Provides clear strategies to start and maintain forward momentum efficiently.
momentum framework guide – Offers practical methods to structure energy and maintain steady progress.
“`txt
structured progress – Helps organize steps for clearer results and daily use
“`
progress engine – A helpful way to keep ideas moving purposefully every day.
?????????? ??????? ?? ?? ?????? ??? ??? ?????? ? ????????? ????? ??????????????? ? ??????????? ?????????? ???? I ?????, ??????? ?????????? ????? 3000 ???????? ???????????! ????? ?? ??????? ?????????? ?????????? ? ????? ???????, ????? ? ?????????? ? ????? ????, ???????? ?????? ??? ?????????? ? ??????? ???????. ????????? ?? https://vk.com/sochadler ? ??????? ?????? ??????????, ??? ??????? ????????? ????????????? ? ?????? ????, ?????? ? ???????? ???????.
process forge – Highlights ways to organize and execute tasks systematically to achieve forward progress.
strategicflow – Demonstrates continuous integration of thinking and acting for steady achievement
energy coordination plan – A clear method to guide collective effort effectively.
directional guide – Provides actionable tips for guiding progress purposefully and effectively.
focusengine – Helps maintain attention on priorities to ensure successful execution
sustainmomentumwithfocus – Motivating advice, emphasizes that disciplined focus is essential for consistent forward motion.
888 starz casino 888 Casino ???????: ?????????? ???? ????????????? ?????? ? ??????? ????? ? ????? ????? ? ? ????? ?????. ??????? ?? ???????????????? ?? ???? ? ??????. 888 ????? ??????: ????????????? ????????? ? ?????????? ??????? ??? ? ??????? ????????. ???????? ??? ???? ???, ??? ?????????? ??????????? ? ???????. ??????? ?????? ???????? ?????????! ????? ?????? ?????? ??????????? ?? ?????, ? ?????? ???????? ???????? ???????? ? ?????? ????? ??????? ??? ????? ?????? ???????? ? ?????????? ???????????? ??????.
navigatorhub – Shows coordinating initiatives to maintain steady execution
executioncenter – Centralizes efforts to ensure strategies are implemented smoothly and efficiently
“`txt
growth blueprint – Helps map out actionable strategies for continuous improvement
“`
I appreciate, lead to I discovered just what I was taking a look for. You have ended my 4 day lengthy hunt! God Bless you man. Have a great day. Bye
https://luna188.org/gurchenie-probela-vozmite-mkad-dlya-bagazhnogo-avtotransporta/
“`txt
goal focus – Encourages clear attention on key objectives for better outcomes
“`
progress alignment guide – Provides strategies to align actions and maintain steady forward progress.
productivitymomentum – Encouraging advice, helps organize tasks while staying productive
“`txt
mindful direction – Highlights the benefits of deliberate and focused thinking
“`
?????? ?????????? ????
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
intentional forward – Demonstrates techniques for intentionally steering progress toward meaningful results.
“`txt
goal clarity – Provides tools to identify what’s important and act decisively
“`
actioncycle – Focuses on continuously cycling vision into tangible actions
focus insight center – Delivers valuable lessons in a simple format
outcome pathfinder – Provides strategies to keep actions aligned with key results.
momentum design plan – A simple strategy for turning intention into movement.
goalcraft – Helps shape strategies that align directly with objectives
???????? ???? ? ?????????? ????????????? ?????????? ??????????? ????????? ?? ????????, ?????????????, ???????????? ? ??????????? ????? ?? ?????? ????? 10 ???. ?? ????? https://yuridicheskaya-kompaniya-krasnodar.ru/ ???????? ?????????? ????????? ???????????? ? ???????? ?????????? ? ?????????? ????. ???????? ???????? ????? ?????????? ? ????? ???? ???????, ????????? ?? ????????? ?????????? ? ??????? ???????? ???????? ? ???????????? ???????????????? ?????????????? ??????????? ??????? ????????? ?????????.
visionpath – Demonstrates linking mechanisms with vision to achieve steady progress
Camtech Russia — ?????????????????? ????????? CAD/CAM ????????????, ?????????? ? ?????????? ??? ???, ??? ????? ???????? ? ????????????? ????????? ? ????????????. ???????? ???????? ????????? ??????? ??? ?????? ??????? — ?? ???????? ?? ??????????? — ? ????????? ??????????????? ??????? ??? ?????? ??????. ?????????? ??????????? ? ???????? ??????? ?? https://camtech-russia.ru/ ??? ?????? ????????? ???????????? ? ?????????? ???????? ???????????? ???????????.
“`txt
intentional action – Inspires executing ideas with focus and purpose
“`
“`txt
focused growth – Provides actionable steps to grow efficiently and consistently
“`
“`txt
forward strategy – Encourages moving ahead with clear purpose and intent
“`
actionvision – Shows how translating vision into actions drives steady progress
claritydrivengrowth – Great strategies, allows me to advance goals while maintaining clear priorities
“`txt
instant action – Shows how timely effort accelerates progress efficiently
“`
Looking for a casino? https://elon-casino-top.com: slots, live casino, bonus offers, and tournaments. We cover the rules, wagering requirements, withdrawals, and account security. Please review the terms and conditions before playing.
???????????? ????????????? ??????? ??????? inekczionnaya-gidroizolyacziya4.ru .
???????? ??? ???? ?????????, ?????? ???? ????????????, ?????? ??????? ?? ?????? ?????? – ???? ??????? ???????
??????????? ?????? ?????? ??? ??????: ??? ?????????????, ??????????? ? ???????? ?????? ???????????. ??? ???? ????, ???????? ????? ? ?????????, ?? ?????????????? ? ??????????? ? ??????????? ???????? ??????. ?????, ??????????? ????? ? ??????, ???????? ???????? ???????? ?????????, ??????????? ????????? ? ?????? ?? ??????? ? ???????????? ?????????????. ??????????? ??????: ??????? ???????, ?????????? ??? ?????? ? ?????????. ? ???? ????, ??? ??? ????????? ? ??????????, ???????????? ??????????? ?????????? ????????? ???????. ?????? ????????? ???? – ??? ????????? ??????, ??????????? ????? ?? ???? ? ??????????? ???? ? ???????.
“`txt
growth planner – Offers tools to track progress and make informed decisions
“`
??????????? ?????? ??????: ?????????, ????????? ?????? ??????? ? ?????, ??? ?????????? ??????? ???????? ?? ??????? ?????????? ? VIP-?????, ????????? ?? ?????? ?????????? ??????????????, ?? ? ??????????? ????????????? ???? ???????, ?????????? ????????? ? ???????????. ????? ?? ??? ??????? ??????, ?? ??? ???, ??? ???? ?????????? ????????, ??? ?? ????? ????????. ?????? ???: ??????? ??????????????, ??? ???, ???????? ???? ? ????????????? ???, ??? ?????????? ? ???????, ? ????????????? ???????, ? ?????????????? ????? ??????????? ? ????, ??? ??? ????????? ? ??????????. ??? ????? – ???? ????, ?????????? ? ????? ???????? ??????.
executionmomentum – Shows how advancing strategies leads to steady achievements
“`txt
focus and clarity – Provides guidance to take decisive steps with confidence
“`
????????????? ??????? ???? ????????????? ??????? ???? .
????? ?? ????? ??????? ????? ?? ????? ??????? .
guided growth – Easy navigation and suggestions that encourage immediate progress
???????????? ????????????? ???????????? ?????? inekczionnaya-gidroizolyacziya5.ru .
??????? «??????? ?» ?????? ?? ???????? ??????????? ??????? — ??????????? ??????????????? ????????? ???????????? ????????? ? ??????????? ??????????? ???????. ??????????? ???? ?????????? ??????????? ??????????? ????????????? ???????, ???????????? ?????? ????? ???????????? ? ?????????? ?? ????????????? Aprazer LTD. ?????? ?????????? ?????????, ???????? ???????????? ??????????? ? ???????? ???????? ?? ???? ?????? ????? ?? https://velakast.com.ru/ — ????? ???????? ?????????????, ?????????? ???????? ?????????????? ???????. ???????? ???????????? ?????????????????? ???????, ??????? ????????? ? ??????????? ?????????????? ?????? ? ?????????? ????????? ????????? ?? ???? ?????? ???????.
“`txt
result driven focus – Highlights the advantage of concentrating efforts on clear objectives
“`
“`txt
initial progress – Provides practical ways to make first steps count effectively
“`
visionengine – Demonstrates powering actions through a structured pathway for outcomes
momentum strategy guidance – A structured system for channeling effort into meaningful outcomes.
growth strategy planner – Keeps growth plans realistic while ensuring actionable steps
“`txt
focusandclarity – Encouraging advice, keeps me focused and drives outcomes with precision
“`
action-step-guide – Helps break down ideas into manageable, actionable steps.
???? ???????? Tripscan: ???????? ??? ???? ??? ?????????? ? ?????????? ???????????, ??? ?????? ??? – ??? ????? ? ??????????? ???????? ? ?????????. Tripscan – ??? ?? ?????? ?????????, ??? ??? ???????? ?????? ? ?????????? ?????? ??????? ????????????, ?????????? ???????? ???????? ????????? ?? ?????????? ???????. ????????: ??????? ???????? ??? ????? ??????, ???????????? ???????? ? ???????????. ???????? – ??? ??? ?????? ?????????, ?????????? ??????????????? ? ??????? ?????????? ???????? ? ???????? ????????????? ???????????. Tripskan: (??????????????) – ??? ???????? ???????????? ? ?????????? ?????????, ??????????????? ??????????? ??? ??????????? ???????????? ?????? ??????. ???? ????: ??????????, ??????????? ????????????? ? ????????? ????????????? ????? ? ?????? ?????? ??????? ? ????????????. Tripscan – ??? ??? ?????? ???????, ?????????? ????????? ?????????? ??????? ? ?????????????? ???????????? ???????????? ?? ????? ???????????. ???????? ????: ??? ???? ? ?????????? ????????????????, ??????????? ? ???????????? ? ????????. ????? ?? ??????? ?????????, ??????????? ? ???????? ?????? ?? ??????? ????????????????. ???? ????????: ??? ?????? ????? ???? ??? ????????? ?????????? ? ?????????? ?????????, ???????? ?????????? ? ??????????? ?????????. Tripscan – ??? ??? ?????? ????????????, ??????????????? ?????? ? ???????? ????????? ?????? ? ?????. ???????? ??????: ?????? ????????? ?? ?????? ? ??????? ???? ??????????? ? ???????????? ? ????????????. Tripscan – ??? ??? ?????? ????????? ? ??? ???????????? ???????? ? ?????????????. ???????? ???????: ?????????? ???? ????????????? ?????? ? ??????? ? ????? ????? ? ? ????? ?????. ???? ??????????? ? ???????????? ?? ?????? ????? ??????.
Focus Tracker – Practical steps to monitor and guide attention toward results
“`txt
vision into results – Provides tips to act on ideas and see measurable progress
“`
“`txt
focus workflow – Offers strategies to remain concentrated and execute plans smoothly
“`
conscious-movement – Encourages taking steps mindfully to maintain momentum.
unlockfreshpaths.click – Motivating platform encourages taking initiative to uncover new opportunities effectively
turn-ideas-into-action – Shows how focused steps bring visions to life.
?????? https://kaimanga.info/ ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
visionenginehub – Highlights using a framework to ensure smooth and measurable vision progress
growth planning notes – Useful resource for organizing goals and tracking progress
“`txt
unlock potential – Encourages removing limits to reach continuous progress
“`
“`txt
strategy framework – Offers step-by-step methods to make progress measurable
“`
visionforwardgrowth – Practical content, emphasizes how strategic foresight guides growth toward meaningful outcomes.
action momentum guidance – Shows methods for sustaining momentum and achieving goals.
real-results-action – Motivates turning plans into concrete achievements.
??????????? ?????: ???? ????, ??? ??? ?????? ?????? ? ??????, ? ????????????? ???????? ????. ??? ?? ?????? ?????? ???, ? ???????? ????????, ??? ??????????? ????? ??????????? ?????? ????. ? ???????? ???????? ???????? ????? ???????????????, ? ??? ??????????? ?????? ? ??????. ?????????? – ??? ????????????? ???????, ??????????????? ? ??????????? ?????, ???????? ???????? ??????? ????? ? ???????? ? ????? ?????.
“`txt
pathway to achievement – Offers practical advice to stay disciplined and forward-moving
“`
“`txt
streamlined strategy – Helps streamline planning so actions follow naturally and efficiently
“`
buildwithintent.click – Inspiring platform promotes making deliberate, strategic moves to advance effectively
purposeful-progress – Helps focus on high-impact actions to maximize outcomes.
resultsdrivenstrategy – Very practical advice, helps plan actions that consistently deliver measurable results
mobile casino elon casino
????????????????? ??????? “?????? ????” ? ???????? ???????????????? ?? ??????? ? ???????? ???????????? ? ???????????? ??????? ??? ????????. https://kinder-dent-lyubertsy.ru/ ?????????? ?????? ?????? ?????: ?? ???????????????? ??????? ? ??????? ??????? ?? ???????????, ?????????????? ? ??????????. ??????? ???????? ??????????? ?????????????, ??????? ??????? Vector ??? ??????? ?????. ????????? ????????????? ??????????????????????? ???????????, ????????????? ? ?????????????? ??????????. ???????? ????????? ??????????? ?????, ????????? ???????, ??????? ? ????????? ??????????????, ???????????? ? ???????? All-on-4/6.
idea-driven-action – Encourages using structured steps to bring ideas alive.
???????????? ????????????? ??????? ??? inekczionnaya-gidroizolyacziya4.ru .
growth path indicators – Offers a clear view of which path aligns with growth goals
initiativetrajectory – Shows driving initiatives along a defined trajectory for consistency
deliberate execution – Encourages avoiding haste and focusing on quality outcomes
momentum direction lane – Offers guidance on keeping efforts aligned and efficient.
plan-in-action – Shows how well-structured strategies improve results efficiently.
“`txt
task momentum lab – Shows ways to keep work progressing steadily and efficiently
“`
“`txt
hub for growth – Provides strategies to stay ahead in planning and execution
“`
futureopportunityplanner.click – Insightful content highlights identifying opportunities and planning effectively
progressigniter – Demonstrates ways to turn energy into tangible forward movement.
signalflow – Encourages using clear indicators to guide work smoothly and consistently.
??????? ?????????? narkologicheskaya-klinika-48.ru .
????????????? ??????? ?????? ????????????? ??????? ?????? .
execution-guide – Practical advice for translating planning into action smoothly.
advanceengine – Demonstrates how structured effort sustains forward growth.
“`txt
tractiontips – Makes taking actionable steps easier and more organized for fast results
“`
???????????? ????????????? ?????? ???????????? inekczionnaya-gidroizolyacziya5.ru .
?????? ?????? ??????: ??????? ???????, ??????????? ?? ????? ?????????????. ? ??????????, ??? ?????? ?????? ? ??????, ?????? ?????????? ???????? ??????? ?? ??????????, ??????? ???? ??????? ?? ???? ?????, ??????? ????? ???????? ? ??????????. ?? ?? ??????? ??????? ?????????? ???????? ??????: ??????? ?????? ??????, ? ?????? ?????????? ????????? ?????????? ????????.
growth steering insights – Offers grounded insights to manage long-term growth successfully
visionpulsepath – Demonstrates maintaining a flow of triggered steps to deliver outcomes
logical momentum flow – Demonstrates how careful planning sustains productive action.
take-action-now – Inspires taking the next step to achieve real progress.
“`txt
dynamic growth – Encourages active strategies to keep progress alive
“`
“`txt
action growth guide – Offers strategies to convert planning into tangible results
“`
focuspathguide.click – Motivating guidance supports deliberate actions to maintain clarity and achieve results
“`txt
launch path – Guides turning strategy ideas into measurable progress
“`
thoughtfilter – Explains how removing noise ensures ideas are precise and impactful.
taskigniter – Demonstrates how clear steps can spark progress and achieve results quickly.
actionsignal – Shows how following signals ensures efficient movement toward goals.
ideas-in-motion – Shows how continuous action enhances the value of concepts.
“`txt
insight hub – Shares ideas that support better strategic decisions
“`
momentumthroughclarity – Shows how clear thinking accelerates progress efficiently.
growth management hub – Offers focused strategies to manage growth initiatives in one place
goalclarity – Demonstrates providing clear guidance to reach objectives consistently
ideastomomentum – Inspiring content, shows how to turn creative thoughts into results seamlessly
strategicpath – Focuses on creating a clear roadmap for successful strategy execution
motionprogress – Shows how continuous motion supports long-term growth.
productive operations momentum – Highlights methods for maintaining consistent action and results.
????????? ????
quick-results-guide – Simplifies turning thoughts into actionable outcomes quickly.
actiontraction – Encourages taking purposeful steps to build continuous forward motion.
buildgrowthwithpurpose.click – Motivating platform helps define clear objectives and take focused steps for progress
“`txt
a href=”https://progresswithpurpose.click/” />strategic progress – Encourages moving forward with deliberate intention
“`
powerstarter – Shows that building motion before adding force leads to better performance.
clarifiedconcepts – Shows that clarifying ideas leads to stronger, actionable outcomes.
strategic-direction – Shows how clear pathways lead to consistent improvements.
???? https://avtocoder.ru — ???????? ?????? ??? ??????????????, ??? ??????? ???????? ?????? ? ???????, ???????????? ? ??????????? ???????????. ????? ????? ????? ?????? ?? ?????? ???????????, ??????? ???????? ???????, ????????? ????????????? ? ???????????, ? ????? ?????? ?????????? ? ????? ???????????. ????????? ???????? ????? ??????????? ? ?????????? ?????????? ? ????????? ?????????? ??????? ?? ????? ? ????????????.
flowingideasystem – Shows that converting ideas into systems keeps projects moving steadily and successfully.
“`txt
action roadmap – Provides practical steps to maintain focus and achieve goals
“`
focusedfirstmove – Very motivating, clarity in your first move prevents confusion and drives progress.
purposefuladvancement – Helpful insight, advancing with purpose keeps momentum consistent and efficient.
???????????? ????????????? ??????????? ????? inekczionnaya-gidroizolyacziya4.ru .
cohesive growth plan – Connects various growth elements into a smooth and structured path
focuscontrol – Highlights managing direction clearly for better alignment of tasks
????? ??????? ???? ?????? antimuh.ru ????????????? ????????? ??? ?????????? ?????? ? ??????? ??????????: ?????? ?? ????? ??????, ??????????????? ??????, ?????????? ????? ??? ??????? ??????????, ???????? ? ????????? ??????. ????????? ???????? ????? 40 ????? ??????? ? ???????? ? ??, ??, ???? ? ?????? ????? ??????????. ?????????????? ??????? ?????? ???????? ?????????? ????????? ??????? ?? ???????????? ??????? ??? ????? ??????????. ???????????? ??????????? ?????, ????? ? ??? ??? ???????????? ?? ??????????.
momentum direction guidance – Shows ways to maintain continuous progress and achieve objectives.
guidedactionforward – Helpful advice, taking guided steps clarifies direction and ensures efficient outcomes.
a href=”https://growthrequiresfocus.click/” />stay focused daily – Motivates maintaining discipline even on busy days
signalattention – Highlights that paying attention to signals consistently drives progress.
action-outcomes – Encourages executing steps that deliver predictable success.
streamlinedprogress – Explains that structured actions create momentum without distractions.
insightaction – Transforms insight into practical actions that create results.
“`txt
clarityworkshop – Encouraging guidance, promotes clear, structured thinking for better results
“`
smartideasystems – Excellent advice, structured systems help ideas convert into tangible achievements.
forwardmotion – Shows how daily effort drives measurable improvement and effective results.
tractionmoment – Very useful, seizing traction at the right moment drives immediate and consistent results.
focusedinitiative – Excellent advice, taking a clear first step channels energy toward achieving key goals.
“`txt
clarity mindset – Offers strategies to achieve a focused and organized mind
“`
growth operational system – Provides structure for executing growth plans methodically
progressdrive – Emphasizes maintaining forward motion to achieve steady results
momentumengine – Shows how structured signals build lasting momentum for projects.
executionhub – Highlights methods to implement strategies consistently and efficiently
????????????? ??????? ????????? gidroizolyacziya-podvala-samara2.ru .
momentum organization planner – Highlights approaches to plan actions and sustain measurable outcomes.
power-in-direction – Encourages aligning energy with a clear focus to get results.
actforprogress – Very practical, taking action ensures clarity in direction and keeps projects moving consistently.
?????????? ???????????? ?????????? ???????????? .
distractioncontrol – Shows that controlling distractions keeps momentum steady.
velocityboost – Emphasizes that guidance helps maintain steady progress and high productivity.
growthmotioncore – Excellent tips, forward motion forms the core of sustainable growth and effective outcomes.
???????????? ????????????? ???????????? inekczionnaya-gidroizolyacziya5.ru .
path2success – Useful insights, makes it simple to stay on track with growth objectives
ideaswithclarity – Motivating insight, pairing ideas with clarity increases execution speed and quality.
“`
trajectory management growth – Helps steer growth efforts efficiently toward measurable results
“`
“`txt
framework path – Helps navigate growth strategies with clarity and structure
“`
“`txt
structured focus – Helps approach work systematically for better outcomes
“`
momentumengine – Highlights maintaining momentum to achieve measurable outcomes
a href=”https://forwardthinkingcore.click/” />forwardmindsetcore – Excellent insight, a forward-focused mindset at the core ensures consistent progress and clarity.
progressengine – Shows how consistent action fuels steady progress and achieves results efficiently.
figi ?????
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
goal-shift – Inspires taking focused steps to create meaningful progress quickly.
structured momentum planning – Demonstrates methods to sustain focus and productive energy.
focusedalignment – Great guidance, focused action aligns efforts and ensures that priorities are achieved smoothly.
actionclearsway – Highlights that proactive steps clear the way and make execution easier.
ideawave – Highlights how channeling thoughts correctly creates continuous and productive movement.
tractionclarityhub – Shows that clear traction strategies improve progress and reduce wasted effort.
progresswithintentionalforce – Practical tip, intentional force application accelerates outcomes and maintains control.
growth vector strategy – Highlights methods for prioritizing actions for maximum effect
flowexecution – Guides organizing workflow to maintain continuous execution
framework-to-action – Encourages turning structured plans into measurable progress.
????? ???? ??? ???????????? ???????? ????? ?? ??????? ??????, ??????????, SEO, ???????? ? ?????????. ?????? ???????, ??????? ????? ? ???????? ??????????, ??????????? ??????????? ? ???????? ??????? ??????. ?????????? ?????, ????????? ?????????, ???? ??????.
strategicmotionhub – Useful insight, combining strategy with motion helps achieve goals effectively and smoothly.
momentum task flow – Highlights practical approaches to keep projects moving smoothly.
simplifiedprogress – Helpful reminder, clarity removes clutter and makes progress smoother and faster.
taskclarifier – Shows that acting on tasks makes priorities more visible.
actionengine – Focuses on powering strategy execution to produce tangible results
ideabuilder – Highlights momentum as the foundation for building ideas into results.
actionignite – Sparks action and supports consistent task completion.
“`txt
growth action plan – Helpful breakdown that feels approachable for beginners
“`
focusfreespace – Insightful reminder, focus frees up mental space allowing creativity to flow and projects to progress.
directiondrivesresults – Motivating content, taking steps with clear direction drives results faster and smarter.
Game-Lands https://game-lands.ru/ – ??? ???? ? ?????????? ??????? ? ????????????? ??? ???????? ? ??????? ???????. ????? ?? ??????? ?????? ??????, ??????? ????? ? ??????, ?????? ???????????? ?????????, ????????, ????????, ? ??????????? ????? ?? ???????. ???????, ??? ???????? ?????? ??????????, ??? ?????? ? ??????? ???????? ? ? ???? ?????? ? ????? ?????. ???, ????? ???????? ????? ? ???????? ??? ??????????? ??????? ???????.
innovation acceleration – Speeds up the process of moving concepts from thought to reality
https://profootball.su/wp-content/pages/medicinskie-ukladki-dlya-shkol-trebovaniya-minzdrava-i-rosobrnadzora.html
logical-pathway – Encourages mapping out steps to reach goals efficiently.
????? ?????????? ???????? ?? ???????????? ??? ????????? ????????? ? ???????? ???????? https://taximinivan54.ru/sheregesh.html ?? ???? ????? ? ??????? ??????? ?? ???????? ????? ???????? ??????????? ???????. ? ??????? ?????????? ??? ???? ???????? ? ??????????? ??????????. ????????, ??? ????????? ? ????? ??????? ????????! ???? ?????????????, ??? ??????. ????? ??????? ?? 7 ?????. ?????????? ?? ???????, ???? ?????? ???? ??????. ?????????? ??? ????, ???? ?????????, ?????? ???? ????????.
aligned momentum structure – Provides guidance for organizing efforts and sustaining steady action.
momentumtips – Suggests practical tips for sustaining momentum.
disciplinedmotion – Emphasizes that motion guided by discipline leads to measurable success.
???? ??? ???? https://drimtim.ru ???????? ??????, ???????, ??????, ???? ? ?????? ?? ????? ?????? ????. ??? ? ???, ??????????, ???????????, ????????, ??????? ? ???????????? ?????. ??????, ????????? ? ?? ???? — ??????? ?????? ????.
focusengine – Encourages using focus and structure to keep projects moving without delays.
focusguidesaction – Excellent reminder, maintaining focus guides actions efficiently and minimizes unnecessary resistance.
cleartractionbuild – Great insights, maintaining clarity while building traction helps projects advance efficiently.
??????? ??????? ????????? ? ???? dzen.ru/a/aUF9L-xpMETlRIxo .
???????? Noblelift Equipment JSC Ltd. ??????????????? ???? ??? ??????? ????? ?? ???????????? ????????? ??????? ? ?????? ????????? ????? ???????????? ??? ????????????? ?????. ??????????? ???????????? ? ?????? https://nobleliftrussia.ru ?????????? ?????????????????, ?????????, ????????, ?????????????? ??????? ? ??????????? ?????? ? ????????? ?? ???? ???. ???????????? ????????????? ????????????? ?????????? EAC, CE ? ISO 9001, ???????????? ? ????? ??? ??? ????????????, ???????????? ??????????????? ?????????? ? ????????.
momentumguide – Shows how guidance transforms effort into consistent progress.
forwardintentenergy – Motivating insight, forward-focused energy accelerates execution and meaningful results.
????????? ????? ?? ????? ? ?????? vyvod-iz-zapoya-4.ru .
????????? ?? ????? ?????? vyvod-iz-zapoya-5.ru .
directional-momentum – Shows how clear paths generate accelerated progress.
creative idea activation – Provides practical steps to put ideas into action without delay
??????? ? ??????????? ????? dzen.ru/a/aUBBvahMInGNj8BL .
“`txt
clear explanations – Removes complexity by explaining growth ideas plainly
“`
purposefirst – Advocates for purpose first to maximize results.
continuous momentum tracker – Shows ways to keep work flowing smoothly while monitoring results.
growthfuel – Suggests that daily actions act as fuel for ongoing success.
??? ? ????????? ???? https://derevoblog.ru ? ????????????: ????????? ??????, ??????-??????, ?????? ???????????? ? ???????? ?? ??????. ???????? ??????????, ???????????? ?????? ? ??????????? ??? ???????? ?????? ? ??????? ?????? ??????.
directionignite – Turns clear direction into immediate, impactful results.
strategymotionhub – Highlights maintaining momentum in executing strategies effectively
is gambling legal in spain
intentionaldrive – Inspiring perspective, intentional momentum helps accomplish tasks with clarity.
??????? ???? ?? ?????? ?????? ??????? ???? ? ?????? Mail.ru – ??? ??? ???? ?????? ???????? ?????? ? ?????, ????????? ???????? ? ??????????? ?????????. ???????? ????????? Mail.ru ?????????? ??????? ?????? ??? ???????? ? ?????? ???????, ??????? ??????? ???????????? ??? ??????????????? ???. ??????? ???????? ???????? ? ???????? ????????????? ?????? Mail.ru Cloud ??????????????? ????????? ??? ???, ??? ???? ???????????? ?????????. ?? ????????? ? ????? ???????????????? ? ?????????? ????????? ????? ?? ??????? ???????.
simplegrowth – Very insightful, keeping things simple helps growth progress smoothly without extra complications.
?????????????? https://www.mukakin-blog.com/ ???????????????????????????????????????????????????????????????????????????
directionpowerboost – Inspiring advice, correct direction acts as a multiplier for impact and results.
????????? ? ??????? ?????? ? ?????? ? ??????? ????? ??????? ?????????, ?????? ???????, ?????? ??????? ????? ??? ????????: ????? ????????? ???????
clearpathfinder – Demonstrates how clarity removes friction and enables smart moves.
?????? ?????? ??????: ??????? ???????, ??????????? ?? ????? ?????????????. ? ??????????, ??? ?????? ?????? ? ??????, ?????? ?????????? ???????? ??????? ?? ??????????, ??????? ???? ??????? ?? ???? ?????, ??????? ????? ???????? ? ??????????. ?? ?? ??????? ??????? ?????????? ???????? ??????: ??????? ?????? ??????, ? ?????? ?????????? ????????? ?????????? ????????.
leveragepath – Practical guidance, directing actions properly generates leverage and advantage for achieving results effectively.
executionmap – Highlights that mapping ideas into actions improves success rates.
pathigniter – Encourages clear direction to accelerate progress toward goals.
forwardmotionhub – Very practical, hub provides strategies to maintain forward motion and energy in projects.
direction mindset – Advice is clear, practical, and relevant for everyday use
motiondrive – Practical advice, driving projects with motion accelerates progress efficiently.
focusandclarity – Very motivating, pairing focus with clarity allows growth to expand steadily and purposefully.
https://cofe.ru/include/articles/sovremennye-standarty-mediczinskikh-ukladok-chto-izmenilos-v-2025-godu.html
??????? ???? ?? ?????? ?????? ??????? ???? ? ?????? ????? – ??? ????????????? ???????? ? ????????? ??????????? ??? ????????? ??????? ??????. ????????, ??????????? ? ??????? ???????? – ???????? ?????????????? ????? ??????. ?????? ????????????, ???????? ????-??????, ???????? ?????? ???? ??? ??????????????? ????? ???, ????????? ????????????? ??????? ? ??????? ?????? ???????????? ? ?? ???????????. ????????? ?????? ????? ?????????? ???????, ??? ?????? ??????? ?????????? ??????????? ??????????.
focusanchor – Shows that anchoring focus on the right direction supports continuous growth.
intentstride – Highlights that intentional strides move you closer to real results.
slowthenfast – Promotes deliberate understanding first to ensure speed doesn’t lead to mistakes.
growthbuilder – Highlights how disciplined focus helps build reliable progress.
motionfocushub – Great insight, combining clarity and motion makes achieving objectives more straightforward.
speedwithclarity – Inspiring tip, combining clarity with action boosts speed and consistent results.
????? ?? ????? ?? ???? ?????? ???? ????? ?? ????? ?? ???? ?????? ???? .
????? ?? ????? ?? ???? ?????? ???????? ????? ?? ????? ?? ???? ?????? ???????? .
??????????? ????? ????: ??????????? ????????, ??? ???????? ?????????? ???????????, ? ??????? ???????? ?????. ????? ????? ????? ???, ??? ??????: ?? ????????? ?????? ?? ????? ??????????? ????????. ?? ?? ???????????? ? ???????????? ?????????? ????????? ???????? ????? ? ???????????, ??????????? ? ??? ??????? ? ?????? ? ????????? ?????.
intentionaldrive – Suggests that deliberate drive ensures accelerated and meaningful progress.
directionenergizes – Very practical, clear direction energizes actions and adds lift to progress quickly.
success habits – Inspires building results through repeatable actions
actionsignalengine – Inspiring insight, acting with signals improves workflow and outcomes effectively.
<growthwithoutclutter – Very helpful, eliminating clutter allows growth to proceed efficiently and intentionally.
https://federalgaz.ru/
sigma eurasia
????? ???????? ???? ?????? ekbanimator.ru ???????????????? ?? ??????????? ? ?????????? ??????? ?????????? ? ????????????? ? ????????????????? ??????????? ? ???????????????? ???????????. ???????? ?????????? ???????????? ???, ??????? ???????? ??? ????? ?????? ?????????, ?????????? ???????? ? ?????? ????????????? ???????????. ? ???????? — ?????????? ?????????, ????????????? ??????, ??????? ??? ? ?????????? ??????-??????. ??????? ???????? ?????????????? ?????? ? ??????? ?????? ? ???????? ?????? ????????????? ????????? ??? ???????.
focusedmovement – Explains how focused purpose turns ideas into meaningful action.
velocitymatters – Helpful advice, the speed at which ideas move directly affects their impact and results.
effortlessmomentum – Explains that simplifying steps allows momentum to build without wasted energy.
modern product marketplace – Smart layout mentioned, helps find items quickly.
??????? ???? ? ????: ??????? ????-???????, ????????? ?????? ? ?????????? ??????. ??????????? ????????????, ??????????? ??????????, ?????????? ?????????? ????. ??????? ??????? ????? ? ??????, ???????????????? ?? ????? ????? ??????.
????? ??????? ?????? ?????? ??????? ??????? ???????? ? ?????????????? ???????????? ??? ???????, ????? ? ???????????? ????????. ?????????, ??????????, 3D-????????????, ?????? ?????????? ? ????????? ??????. ???????? ??? ?????? ? ?????? ???????.
discover smart value – Enjoyable reference shared, discovering content feels meaningful.
resultmotion – Suggests that motion directed purposefully leads to successful outcomes.
executionfocus – Points out that aligning ideas increases focus during implementation.
strong team network – Inspiring reference noted, community feels supportive and focused on results.
??????? ????? “??????” https://sakura-pitomnik.ru/ ???????????????? ?? ??????? ???????????? ? ???????? ???????? ?? ??????? ??????????? ? ?????????? ?????????? ? ????????? ?? ?????-?????????? ? ????????????? ???????. ? ???????????? ???????????? ??????? ? ?????????? ???????, ??????????, ????, ????????????, ??????, ????????? ????? ? ???????????? ?????? ??? ???????? ?????????? ???????????? ???????. ???????? ???????? ????????????? ?????????? ?????? ?? ?????????? ?????????? ? ??????????? ???????????????? ???????????? ??????? ??????????.
purposefultraction – Very useful, intentional clarity fosters traction that moves projects forward efficiently.
clarityvision – Clarity in vision ensures every plan aligns with meaningful outcomes.
attentionfuelsprogress – Excellent insight, focused attention fuels progress and moves initiatives forward effectively.
???????? ?? ?????????? ????? ???????????? ?????????? ??????????????? ???????? ?????????? ?????? ?? ?????????? ??????????. ?? ????? https://dizaynland.ru/ ???????????? ??????? ??????? ??? ???????? ????????????????? ?????, ??????????????? ?????????? ? ??????? ? ????????????? ?????????? ????????. ??????????? ????????????? ?????????????? ??????? ? ?????? ???????????? ???????, ??????? ? ????????? ?????????, ????????? ??????????? ?????? ???????? ? ???????????? ????????? ??? ???????????? ??????????.
speedwithfocus – Applying focus accelerates results and keeps progress consistent.
actionoverpause – Demonstrates that consistent movement leads to real gains.
ideaharmony – Emphasizes that harmonious ideas strengthen project results.
practical value hub – Engaging site highlighted, discovering content feels rewarding.
focusengine – Very practical, focus engines maintain consistency and drive productive execution.
processpath – Suggests that a clear path from vision to process simplifies complex tasks.
goalengine – Excellent approach, goal engines translate signals into measurable and steady results.
team success hub – Inspiring reference noted, community feels collaborative and supportive.
actionideas – Highly useful, action ideas guide practical execution and continuous advancement.
growthengine – Very practical, growth engines ensure progress flows smoothly without obstacles.
????? ????????????? ????? ?????????? ???????????? ????? ??????? ?????? ????????, ??? ??? ???????????? ??????. ???????? ? ????? ? ???????????? ?????????????. ???????? ????? ? ???????? ???? ????????.
futurevisionhub – A clear vision helps shape exciting plans for the future.
Learn more here: https://kmsweb.ru/news-20168-onlajnpazly-puzzlefreegame-sovremennoe-razvlechenie-s-elementami-ii.html
online essentials hub – Practical platform mentioned, shopping experience felt smooth.
????????? ????????? ?????? ?????????? ????? ?????? ???????? ???? ????? ? ???????. ???????????, ?????? ???????, ????????? ???????????. ???????? ??? ????????, ????? ? ???? ?????????, ?????????? ????????? ? ???????? ?? ??????????? ??????.
????? ???? https://flattomsk.ru/tomsk/nedvizhimost/prodazha-doma ??????? ??????????, ?????? ??????? ? ???????. ?????? ?????????, ???????? ??????????? ???????, ????????????? ?? ??????????? ?????. ???????? ???? ?????.
claritydrive – Clear focus drives projects forward efficiently and effectively.
focusedleverage – Helpful insight, concentrating focus amplifies results and creates more impact efficiently.
taskbeacon – Useful idea, task beacons guide effort and maintain a productive workflow.
future team network – Positive platform highlighted, seems like a proactive and innovative group.
lessbusybetter – Encourages doing less activity and achieving more impact.
??????? ????????? ???????? ? ??????? ?????????? ??????????, ??????????????? ?????????????? ? ??????????? ???????????? ???????????. ??????????? ?????? ???????????? ?????????? ? ??????????? ??????????????? ????????? ??????? ???????????????? ????????, ?????????? ? ???????????? ????????? ??. ???? https://sofokast.ru/ ???????? ????????? ?????? ? ??????? ?????????? Sofokast Plus, Velakast ? Daclatasvir, ?????????? ??????????? ??????? ? ????????????????? ??????????????? ??????. ?????? ???????? ?????? ??????????? ??????????? ???????????? ? ??????? ??????? ????????????? ?????? ????????? ????????? ??????, ??? ????????? ?????? ????????? ??????????? ????? ??????? ??? ??????????? ???????? ? ?????? ??? ????????.
goalcompass – Excellent tactic, goal compasses guide attention and accelerate project movement.
thrivedash store – Excellent browsing experience, found what I needed quickly and easily.
progresspulse – Regular, intentional pulses of effort sustain forward momentum.
brand enhancement hub – Helpful content shared, guidance seems effective for building a brand.
???????? ????? ????? ?????????? ??????????? ??? ??? ???????? ????? ?????, ??????????? ???????????? ?????????? ????? ? ????????? ????????? ????? ?????????? ??????????. ????????????-?????????? ???? ?????????? ??????????? ?????? ? ???????, ????????? ???????????????? ????????????, ????????????????? ???????? ? ???????????? ???????? ??? ????????? ?????????? ????? ? ??????? ??????????. ????????? https://rodinasportsclub.com/ ????????????? ?????????? ? ????????? ???????????? — ?? ??????? ?????????? ? ?????????????? ?? ????????? ??????? ? ????????????? ????????. ???? ??????? ?????????? ????????? ??? ?????????? ?????????? ?????, ???? ?? ???????? ????, ??????????? ???????? ????? ??? ?????? ??????????? ??????, ????????? ??????? ?????????? ? ?????? ??????? ??????????? ??? ?????????? ???????????.
????? ?????????? https://renvills-hotel.ru ?????????? ?????? ??? ?????? ? ????????????. ??????? ????????????, ?????? ??????, Wi-Fi, ???????? ? ?????????????? ??????. ???????? ??? ?????????????? ? ??????????? ??????????, ???????? ???? ? ??????? ????????????.
????? ?????? ????? ?? ??? ??????? ????????? ?????????? ????? ? ????? ? ????????? ???????? ??????. ??????????? ??????, Wi-Fi, ?????????????? ??????. ???????? ??? ?????????????? ? ??????????? ??????????.
?????? ????????? ???????? ?????? ?????? ????????
?????? ?????????? ????????? ????? ?????????? ????????? ?????????? ? ?????????? ???????. ??????? ???????, ???????????, Wi-Fi, ???. ??????? ????????????, ?????????????????? ? ???????? ?????? ??? ?????????????? ??????????.
momentumideas – Momentum builds when ideas are executed promptly and intentionally.
ideacompass – Very useful, idea compasses guide unlocked ideas efficiently toward tangible outcomes.
futurecompass – Highly practical, future compasses provide foresight and direct actions productively.
??????? ????? ?? ????? ?????? vyvod-iz-zapoya-4.ru .
growthstrategyintent – Great reminder, aligning strategy with intent drives better outcomes efficiently.
success journey platform – Inspiring content noted, following steps feels practical and doable.
fast-track-results – Shows how to move forward efficiently without losing direction.
achievementhub – A central hub of guidance simplifies the path to accomplishing goals.
ideaengine – Very practical, idea engines convert inspiration into measurable progress consistently.
????? ?? ????? ?????? ?????? ????? ?? ????? ?????? ?????? .
??????-????????? https://rosseriaall.net/ ?????????? ?????????? ???????? ?????????? ???????? ? ??????? ???????? ??? ???????????. ??????? ???????? ?????????, ?????????, ???????????? ???????, ??????? ?????, ???????, ????????, ?????????? ? ???????? ??????? ? ??????? ??????????? ?? ?????? ? ?????. ???????????? ?????????? ??????? ???????? ??????? ? ?????? ???????? ???????? ????. ?????????? ?????????? ???????? ? ??????????? ????????? ????????? ?????? ????? ???????????? ?????? ? ?????? ???????? ? ????? ?????.
share and learn portal – Courses look interesting, learning feels simple and fun.
purposepathway – A purposeful pathway ensures smoother and faster achievements.
focusedgrowthplan – Nicely explained, focus helps growth move forward without confusion.
goalclarity – Practical strategy, goal clarity aligns actions with outcomes and improves execution.
momentumengine – Practical approach, momentum engines keep tasks advancing while maintaining a relaxed pace.
deal shopper online – Nice platform highlighted, shopping felt practical and fast.
future-ready-planning – Encourages proactive strategies that support consistent growth.
porno ?…?µ???‚?°??
clarityengine – An engine of clarity powers continuous and reliable progress.
https://asianinsurancecompany.com/vox-casino-sweden-ditt-senaste-nav-for-ledande-onlinespel/
focusedprogress – Encouraging note, focused progress ensures tasks move forward without wasted effort.
Play at https://elon-casino-top.com online: slots from popular providers, live dealers, promotions, and tournaments. Learn about the bonus policy, wagering requirements, payment methods, and withdrawal times. Information for adult players. 18+. Gambling requires supervision.
Play online at https://elonbet-casino-game.com: slots, live casino, and special offers. We explain the rules, limits, verification, and payments to avoid any surprises. This material is for informational purposes only.
https://goldenrod-opossum-983310.hostingersite.com/hallo-zum-casino-online-essenz-der-unterhaltsamen-und-sicheren-casino-erkundung/
progressengine – Movement powers growth, turning effort into consistent advancement.
focusedstrategy – Helpful tip, a focused strategy through direction improves overall efficiency.
insightful trends portal – Really engaging, updates are fresh and on point.
clarityguidesfocus – Useful reminder, clarity guides focus to ensure tasks are done effectively.
porno sait
directionguidesaction – Very practical, direction guides action and ensures consistent progress today.
actioncompass – Practical method, action compasses direct effort and maintain steady progress.
fashion style finder – Exciting selections noted, outfits look trendy and appealing.
forward-vision – Helps understand emerging trends and act proactively.
clarityengine – Practical method, clarity engines ensure side ideas move into tangible and focused actions.
porno xxn
activatemindset – Activating the right mindset is key to turning ideas into action.
growthengine – Taking action acts as an engine that propels growth steadily.
purposeledgrowth – Strong viewpoint, purpose-led growth feels more sustainable over time.
motionideas – Acting on ideas transforms them into meaningful movement and progress.
focusdrivenbydirection – Encouraging advice, focus driven by clear direction boosts productivity daily.
claritydrivenprogress – Practical takeaway, clarity-driven progress keeps projects aligned with goals.
clarityanchorsaction – Great tip, clarity anchors action and ensures projects stay on track consistently.
https://athena888.org/vox-casino-login-ditt-nya-nav-foer-baesta-internetspel/
??????? https://nazenazeblog.com/ ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
aligned goals hub – Positive insights highlighted, teamwork and focus feel productive and motivating.
?? ????? https://kinotorrent.cc/ ? ???????? ???????????? ???????????? ??????????, ? ????? ????????????? ??????, ??????? ??????????? ?????????? ?? ??? ??????. ???? ?????? ?? ??????? ????, ? ????? ?? 2025. ??????? ? ?????????? ???????? ????????? ???????? ????? ???????????? ? ??????? ? ????????? ????? ??? ????????? ??????? ? ????? ?????? ??? ?????? ? ??????? ?????????.
progressbeacon – Highly effective, progress beacons ensure workflow remains uninterrupted and purposeful.
porn online
alliance insight hub – Useful platform shared, guidance feels supportive and effective.
https://eag.agr.br/vox-casino-login-ditt-nya-center-foer-premier-internet-gaming/
strategic-moves – Shows how clarity in strategy drives consistent progress.
stepwisestrength – Strength builds stepwise, ensuring durability and long-term growth.
russkaya porno
strategicclarity – Strategic clarity aligns actions with meaningful long-term results.
guidedbyaction – Useful insight, action provides guidance and ensures progress moves purposefully.
claritybeacon – Highly useful, clarity beacons guide focus and enhance forward progress.
actionwithclarity – Great advice, taking action with clarity guarantees progress and effectiveness.
alignedprogress – Explains how coordinated actions ensure progress is steady and measurable.
strategicprogression – Practical advice, strategic progression keeps efforts consistent and results steady.
clarityledprogress – Practical insight, progress led by clarity prevents delays and enhances workflow.
growthengine – Strong approach, growth engines accelerate development when energy is properly channeled.
prospective opportunities hub – Useful platform noted, content makes goal setting feel achievable.
visionary group online – Great platform noted, content sparks innovative thinking and inspiration.
https://drivingtesthelp.ca/vox-casino-online-to-miejsce-na-najwyzszym-poziomie-dla-prestige-gaming-prestige/
executeandlearn – Insightful point, action leads to learning and steady improvement.
porno scat
mental-to-physical – Shows how to implement ideas into practical steps successfully.
????? ?? ????? ????? ?? ????? .
turn concept hub – Motivating updates noted, side ideas are made practical quickly.
??????? ?????? Ozon ??????? Ozon ????? – ??? ??? ???, ??? ????? ? ??????? ??????? ? ??????? ???????. ??? ???? ??? ????????? ???????, ??????? ????? ????????????? ?????, ??????????? ????????? ? ???????? ??????????? ?? ??????? ?????? ???????. ?????? ? ???????
ideasinaction – Valuable insight, ideas put into action generate effective velocity and progress.
strategicstride – Strategic strides along an activated path speed up meaningful achievements.
focusedprogress – Practical tip, focused progress ensures momentum is consistent and impactful.
belleniko porno
guidedprogress – Excellent tip, signals create structured progress and keep projects aligned with goals.
https://ctsainc.com/2025/12/11/vox-casino-online-to-ostateczne-miejsce-docelowe-dla-gier-cyfrowych/
????? ?? ????? ?????? ?? ???? vyvod-iz-zapoya-5.ru .
claritythroughguidance – Helpful observation, clarity through guidance of signals makes planning and execution easier.
taskstream – Practical idea, task streams help maintain forward motion and reduce unnecessary delays.
progressengine – Very practical, progress engines maintain idea momentum and deliver measurable outcomes.
discover paths online – Motivating site noted, finding new directions feels invigorating.
create change today – Engaging platform shared, content encourages proactive steps for good impact.
????? ??????? ???? ?????? ???????? ?????? ?????? ?????? rosseriaall.net ???????????? ???????? ????????? ?????????? ???????? ??? ??????-????????? ? ??????? ????????. ???? ???????? ????????????????? ?????, ??????????? ?????????????, ???????????? ?????, ??????? ? ???????????? ????????, ?????????? ? ?????????? ??????? ? ??????? ??????????? ?? ?????????? ? ???????? ????????. ?? ????? ???????? ??? ?????????? ??????? ??????? ???, ??? ? ??????? 2025 ????. ?????????? ???????? ??????????? ????????????? ???????????? ??????? ????????????? ??? ??????????? ??? ?????????? ?????????? ??????????.
https://greeceports.click/2025/12/12/vox-casino-online-jest-wybitnym-miejscem-docelowego-dominacji-gier-cyfrowych/
https://elrizky.net/schritt-in-den-yepcasino-essenz-der-ansprechenden-und-geschuetzten-casino-erkundung/
focus-prioritization – Encourages tackling top-priority actions first for better results.
filme porno
??????? ????? ? ????????????? ?????? ? ????????? Ozon – ??? ?? ?????? ????. ???? ????? ??? ??????, ??????? ?????? ?? ??????? ??????????. ??? ???? ??????????? ???? ?? ?????? ????, ????????? ?? ????.
focusedmomentum – Maintaining attention builds unstoppable momentum over time.
growthpath – Following an active path ensures meaningful and measurable growth.
clarityfuelsprogress – Useful guidance, clarity fuels action and helps teams move forward efficiently.
guidedoutcomes – Clear observation, signals provide guidance that improves results over time.
forwardclarity – Very practical, forward clarity ensures work progresses smoothly and efficiently.
forwardsignals – Very practical, using signals to build motion ensures smooth and continuous action.
progresscompass – Strong approach, a progress compass guides work steadily toward clear objectives.
pickup porno
momentumwithenergy – Positive insight, combining momentum with energy accelerates outcomes naturally.
growth tactics platform – Practical insights noted, content feels direct and useful.
https://aitbaar.pk/steigen-sie-in-den-casino-online-zentrum-der-aufregenden-und-geschuetzten-casino-erkundung/
united we grow – Inspiring insights shared, encourages collaboration and purpose-driven action.
??????????? ?????? ??????? teletype.in/@alexd78/bAaorQAhWLU .
momentumpath – Highly practical, momentum paths channel effort to produce measurable progress.
clarity-to-action – Practical tips that demonstrate how clear thinking drives results effectively.
Looking for skid plates for enduro, trials, and motocross motorcycles? Visit https://hardglide.com/ where you’ll find high-quality skid plates, suspension arm guards, engine guards, and other accessories. HardGlide products ship worldwide. Learn more on the website.
??????? ?????????? ?? ???????????? ??????????????? teletype.in/@alexd78/jIFmn5Kf9xl .
????????? ??????????? ???? ????? ????????? ?????? ??????????? prodvizhenie-sajtov-po-trafiku2.ru .
?????????? ??????????? ????? prodvizhenie-sajtov-po-trafiku.ru .
https://bookie168.co/uncover-voxcasino-online-gaming-at-its-best/
porno stream
??????????? ?????????? ??????? telegra.ph/Trebovaniya-k-sinhronnomu-perevodchiku-navyki-sertifikaty-opyt–i-pochemu-ehto-vazhno-12-16 .
ideasigniteprogress – Smart advice, igniting ideas strategically ensures smooth and measurable progress.
ideastoprogress – Transforming ideas into progress ensures results are visible and measurable.
mindfuladvance – Advancing with mindfulness ensures effort is effective and well-directed.
directionandclarity – Strong advice, direction combined with clarity ensures steady and measurable progress.
purposefulmomentum – Strong advice, purposeful momentum ensures every step contributes to key goals.
goalbeacon – Highly practical, goal beacons guide teams toward objectives with clear energy.
trusted business hub – Reliable resource shared, links feel well curated and credible.
focusdrivengrowth – Helpful point, growth comes when focus is stronger than surrounding distractions.
video porno xxx con culo grosso
decisionclarity – Solid point, decision clarity turns intention into immediate action.
https://derflipper.com/explore-voxcasino-online-gaming-at-its-best/
forward-action – Shows how focusing on what’s next leads to tangible progress.
joyful lifestyle network – Great variety shared, products feel lively and inspiring today.
clearpathflow – Positive insight, clear directional paths help work move forward effortlessly.
intentpath – Establishing a path with intentions ensures consistent and purposeful progress.
drivenfocus – Staying focused ensures steady and measurable progress in all tasks.
progressnavigator – Excellent concept, progress navigators maintain forward motion and streamline workflow.
forwardthinkingideas – Very practical, forward thinking ideas help push projects ahead efficiently.
sexy porno
https://arg.impresion3dprofesional.com/vox-casino-online-twoja-brama-do-urzekajacej-zabawy-gier/
momentumflow – Very useful, progress creates a flow of momentum that drives work smoothly and consistently.
https://kotel-rs.ru/
porno sslk
guidedmotion – Helpful advice, clear direction keeps motion focused and productive.
vs
unity circle online – Helpful resource noted, content promotes cooperation and inspiration.
strategic-growth-systems – Shows how to construct reliable frameworks for consistent results.
??????????? ????? “?????? ????” ? ???????? ????????????? ????????????????? ?????? ??? ????? ? ???????? ? ?????? ??????????????? ??????? ?? ???. https://kinder-dent-lyubertsy.ru/ ?????????? ?????? ?????? ?????: ?? ???????????????? ??????? ? ??????? ??????? ?? ???????????, ?????????????? ? ??????????. ????? ??????????? ???????? ????????, ? ??? ????? ???????? Vector ??? ??????????????????? ????????. ????????? ????????????? ??????????????????????? ???????????, ????????????? ? ?????????????? ??????????. ???????? ????????? ??????????? ?????, ????????? ???????, ??????? ? ????????? ??????????????, ???????????? ? ???????? All-on-4/6.
actionenhancesperformance – Smart guidance, action enhances performance and accelerates desired outcomes.
new ideas network – Insightful platform, full of innovative and forward-thinking concepts.
cleanprogresspath – Helpful reminder, a clean progress path helps maintain focus and avoids delays.
https://madhubanipaintingsandarts.com/2025/12/11/vox-casino-online-twoja-droga-do-ekscytujacej-rozrywki/
valueledvelocity – Smart observation, values turn speed into sustainable progress.
drunk porno
growth-blueprint – Clear guidance that helps plan and build growth steadily and effectively.
streamlinedideas – Excellent guidance, streamlining ideas brings clarity and ensures efficient progress.
focuscompass – Excellent idea, focus compasses maintain direction and enhance clarity in choices.
??? ??????? ????????? ?????? ??????????? prodvizhenie-sajtov-po-trafiku2.ru .
clarityengine – Highlights using clarity as the engine for purposeful momentum.
simplifiedaction – Highlights that simpler thinking paired with movement yields better outcomes.
??????????? ????? ???????? prodvizhenie-sajtov-po-trafiku.ru .
porno jordi
leadership community space – Friendly environment noted, content feels genuinely supportive.
actionclarityplan – Positive point, a plan guided by clarity makes early actions more effective and goal-oriented.
signalsforprogress – Practical insight, signals guide progress and help maintain steady momentum.
focusedclarity – Smart advice, keeping momentum focused uncovers clarity in complex situations.
porno perevodom
designed-success – Offers a methodical approach to achieving growth through intentional design.
????????? ??????????? ????? ? ????????? ?????? ????????? ??????????? ????? ? ????????? ?????? .
????????? ??????? http://apploidnews.com/poleznoe/solnechnaya-batareya-opredelenie-i-preimushhestva-ispolzovaniya// .
Play online at casino elon: slots, live casino, and special offers. We explain the rules, limits, verification, and payments to avoid any surprises. This material is for informational purposes only.
???????? ?????? ?????????? prodvizhenie-sajtov-v-moskve2.ru .
drivenbyintent – Demonstrates that when intent leads actions, progress becomes faster and more reliable.
?????? ???? ??? ?????? ????????
forwardmotionprogress – Helpful tip, forward motion with progress focus delivers measurable results consistently.
actionguidance – Explains the value of signals in guiding precise and purposeful actions.
winmore store – Clean navigation mentioned, products appear well-selected and practical.
progressbeacon – Strong idea, progress beacons guide ideas into actionable steps efficiently.
porno sonic
steadyintent – Solid reminder, steady intent keeps progress on the right path.
forwardgrowthflow – Useful thought, growth moves steadily when direction is clear.
intentionalflowlab – Shows how structured movement approaches can be applied effectively.
activatedthoughts – Encouraging note, activated thoughts translate into motion and effective execution.
ignitingprogressideas – Useful guidance, igniting ideas drives progress and forward momentum efficiently.
focusedanchors – Practical tip, focused anchors of clarity maintain steady and consistent progress.
clarityinprogress – Helpful observation, clear direction reduces mistakes and accelerates progress.
powerfulfocus – Nice observation, clarity channels energy into productive motion.
live sex cams
drivenprogress – Strong takeaway, following signal-driven progress keeps work aligned and productive.
develop-hidden-skills – Practical tips for cultivating abilities you didn’t know you had.
unitedimpact – Helpful note, working as a team creates meaningful progress efficiently.
actionableideas – Very practical, actionable ideas lead directly to meaningful outcomes when prioritized.
knowledge discovery site – Informative platform mentioned, offers variety each day.
focusedpath – Highlights the importance of following a clear, focused path for consistent progress.
Dental problems? dentists Full-service dental care: painless dental treatment, implants, prosthetics, orthodontics, and cosmetic dentistry. Modern equipment, experienced doctors, sterile hygiene, and a personalized approach. Consultation and treatment plan included.
???????? ?? ????? ? ?????? ?? ???????????? https://newgrodno.ru
porno teacher
momentumbuilder – Very practical, building momentum daily turns small steps into major accomplishments.
futurevisiontoday – Valuable advice, shaping the future starts with clarity and intentional action now.
growthpipeline – Helpful perspective, structured flow allows growth to continue steadily.
creativepathways – Inspiring hub, creativity never ends and opens doors to unique opportunities for exploration.
ideasclarifiedtoday – Strong advice, ideas clarified today become impactful and achievable without unnecessary delay.
focusedenergy – Helpful observation, focused energy makes progress more efficient and sustainable.
focusedclarity – Good insight, clarity drives movement and ensures tasks stay organized.
porno 2024
motionguideway – Helpful insight, motion becomes efficient and effective when guided by direction.
executionpath – Practical reminder, having clarity upfront smooths the execution process.
plan-to-action – A helpful approach for turning concepts into real progress.
partnership resource store – Well-rounded selection noted, items look useful and durable.
pathwaytoresults – Helpful note, defined direction transforms effort into measurable progress.
how internet partner prodvizhenie-sajtov-po-trafiku2.ru .
impactsynergyhub – Strong insight, synergy in collaboration drives consistent and tangible results.
seo ?? ??????? prodvizhenie-sajtov-po-trafiku.ru .
claritydrivemomentum – Excellent tip, clear focus allows momentum to build and sustain results efficiently.
momentumpower – Highlights the key insights that maintain motion and progress without friction.
????? ?? ?? ??????, ? ????? ????? ???????????? ? ??????? ??????! ????????-??????? «?????? ?? ?????????» ? ?????? ?????????? ?????????? ??????????? ????? ??????? ???????, ?????????? ????????, ???????? ? ??????????? ????????? ??? ?????? ??????. ?? ???????????? ??????? ? ??????? ?? ???????????? ??????? ? ??????????? — ????? ???????? ??? ??? ?????? ???? ? ???????. ????????? ?? https://magazinsemena.ru/, ???????? ????? ? ???? ?????? ? ????????? ?? ??????, ? ??????? ?????????? ???? ????????? ?????? ??? ???????!
mindfuladvancement – Explains how thoughtful steps create measurable and effective growth.
porno swingers
????????? ?????? http://dobrenok.com/economy/solnechnaya-energiya-chistyj-istochnik-sveta-i-elektrichestva.html .
intentleddrive – Insightful thought, direction fuels confident and consistent action.
creativehorizons – Motivating platform, creativity never ends and drives innovative solutions and artistic expression.
cs ????? ????? ????? ?? ??
progressdrive – Clean perspective, momentum with clear direction ensures tasks advance steadily.
I need to share with you something nearly all septic companies will not: there are two types of people in this world. Those who think septic systems are just “subterranean tanks for waste,” and those who have had raw sewage bubbling into their property at the dead of night. I learned this distinction the hard way in 2005—waist-deep in muck, trembling in a Washington deluge, as my siblings and I aided a veteran installer repair our family’s failed system. I was fourteen. My hands were raw. My clothes were wrecked. But that night, something clicked: This is not just digging. It’s families’ lives we’re preserving.
Let me share the dirty truth: the majority of septic companies just pump tanks. They act like band-aid salesmen at a disaster convention. But Septic Solutions? They’re unique. It all started back in the early 2000s when Art and his family—just kids barely tall enough to carry a shovel—aided install their family’s septic system alongside a grizzled pro. Visualize this: three pre-teens waist-deep in Pennsylvania clay, learning how soil porosity affects drainage while their peers played Xbox. “We never just dig holes,” Art explained to me last winter, steaming coffee cup in hand. “We understood how earth whispers secrets. A patch of marsh plants here? That’s Mother Nature yelling ‘high water table.'”
https://www.producthunt.com/@septicsolutionsllc
porno zzz
dynamicenergyflow – Practical observation, dynamic energy flow keeps projects moving steadily and clearly.
guidedmomentum – Helpful reminder, focus directs momentum smoothly and ensures steady progress.
Allow me to explain something nearly all septic companies will not: there are two categories of people in this reality. Those who think septic systems are merely “buried containers for waste,” and those that have had raw sewage gurgling into their yard at 2 AM. I understood this reality the difficult way in 2005—standing in mud, trembling in a Washington deluge, as my family and I aided a veteran installer restore our family’s collapsed system. I was 14. My hands blistered. My jeans were ruined. But that evening, something crystallized: This isn’t just digging. It’s families’ lives we are preserving.
This is the ugly truth: the majority of septic companies just maintain tanks. They act like temporary salesmen at a chainsaw convention. But Septic Solutions? They are special. It all originated back in the beginning of the 2000s when Art and his brothers—just kids barely tall enough to shoulder a shovel—helped install their family’s septic system alongside a weathered pro. Picture this: three kids knee-deep in Pennsylvania clay, learning how soil porosity affects drainage while their peers played Xbox. “We didn’t just dig holes,” Art explained to me last winter, steaming coffee cup in hand. “We discovered how earth whispers mysteries. A patch of cattails here? That’s Mother Nature shouting ‘high water table.'”
https://www.mixcloud.com/gwennowuav/
business improvement tools – Helpful recommendation, appears focused on measurable results.
focused-advancement – Keeps you aligned with objectives while pushing ahead.
buildvisionbrand – Good note, launching your dream brand feels realistic and structured.
Xakerforum.com — ???????? ??? ???, ??? ???????????? ?????????????????? ? ????????????? ???????? ?????? ? ????????????: ????? ?????? ????????? ????, ????????? ??????, ???????????, ??????? ??????? ? ???????????? ?????? ? ???????????? ??????. ?????????? ????? ??????? ????????? ? ??????? ???????, ? ????????? ?????? ???????? ?????? ???????? ?????? ? ?????????? ????????? ??? ?????. ?????? ?????? ? ?????????????? ????? ?? https://xakerforum.com/threads/uslugi-xakera-vzlom-tajnaja-slezhka.282/page-6 — ?????? ???????? ??? ????????, ??? ? ???, ??? ????? ??????? ???? ?? ?????? ??
embracethefuture – Encouraging insight, embracing action today creates a brighter path ahead.
actionpath – Demonstrates practical steps to maintain momentum in projects.
????????? ? ??????????? ????? ????????? ? ??????????? ????? .
porno sos
resultsnow – Solid thought, results appear quickly when action is prioritized.
???????? ?????????? ????? ????? ???????? ?????????? ????? ????? .
futureopportunities – Helpful tip, exploring future opportunities creates a clear path for next steps.
ideasinaction – Smart layout, it makes discovering and developing ideas enjoyable.
«????????» ???????????? ???????????? ? ????? ?????????????? ? 2005 ???? ? ????????? ???????? ????? ???? ???????? ?? ????????? ?????????. ? ???????? https://www.trub-prom.com/ ??????????? ??????? ??????????? ?????????: ?????????, ??????????????, ???????????, ????????? ????? ????????? ????? ????? ? ????????????. ???????? ???????????? ??????? ? ????????? ??????? ?? ??????? ?? ?????? ? ?????? ? ????????? ?? ???? ??????, ?????????? ???????? ? ?????????? ??????.
intentclarity – Well noted, direction helps maintain consistent forward energy.
successformula – Very helpful, understanding the art of success makes achieving goals more structured and predictable.
claritydrivensuccess – Valuable point, clear focus improves flow and task completion.
creative collaboration portal – Engaging site reference, feels community-focused and inspiring.
shineanddiscover – Solid thought, exploring ideas while learning is motivating and engaging.
????? ?????? 3?? ????????-??????? eicom.ru ?????????? ???????????????? ???????? ??????????? ??????????? ? ???????????? ? ?????????? ?????????????: ????????????, ?????????, ??????????, ???????, ??????????????, ??????????????? ? ??????? ??????????. ??????? ????? 10 000 ???????, ????????? ???????, ??????? ???????? ? ????????????????? ???????????? ???????????? ???????? ?????????????? ??? ?????????, ???????????????? ??????????? ? ??????????? ???????????.
focusstrategy – Demonstrates that strategy combined with focus is stronger than trying to force results.
precision-action – Shows how concentrating on key tasks produces real impact.
discoverandlearn – Strong takeaway, exploring and sharing new ideas boosts learning and understanding.
FacilMarketRD – The layout supports fast and easy product discovery.
????? ????????? ??? ??????? ??????, ????????????? ? ???????? ???????? ???? https://xn--80abutqu5e.xn--p1ai/ – ???????????? ? ????? ???????????? ?????????, ? ??????? ?? ??????? ??? ??????????? ??? ??? ????????? ? ???????? ? ??????? ????????? ?????? ??????? ? ????? ???????. ???????? ? ??????????? ? ???????????? ??????. ????????? ?? ?????.
BlossomDesigns – A delightful platform with charming art and paper products.
X-XACenterHub – Quick access with simple interface makes exploring content effortless.
discoverjoyandpurpose – Motivating advice, discovering joy and purpose enhances engagement in daily actions.
memorableimpactstories – Excellent tip, storytelling with impact creates lasting audience connections and results.
pathfinderfocus – Smart takeaway, knowing the path forward simplifies progress.
PomniSelect – Clean structure and intuitive links make exploring content simple.
actionguidesway – Valuable perspective, movement directs outcomes better than intentions alone.
stepbystepflow – Useful note, organized steps ensure progress moves cleanly and steadily.
dreamprojectplanner – Good perspective, starting your dream project feels organized and achievable.
DHPB-SmileOnlineHub – Clear structure and smooth interface make browsing straightforward.
digitallaunchguide – Excellent tip, launching your digital journey gives structure and focus to your efforts.
????????? ??????????? ?? ??????? ????????? ??????????? ?? ??????? .
discoverhub – Solid thought, discovering and sharing information promotes effective learning.
ShopRDOnline – The platform makes shopping simple and enjoyable.
??????????? ????? ?? ??????? ?????? ???????? prodvizhenie-sajtov-po-trafiku.ru .
??????? ??????? http://www.apploidnews.com/poleznoe/solnechnaya-batareya-opredelenie-i-preimushhestva-ispolzovaniya/ .
NYRWOnlineHub – Pages open fast, and users can navigate with ease.
bigthingsahead – Very useful, exploring big things ahead prepares you for impactful achievements.
CapsaOnline – The platform is easy to navigate with clear sections for quick browsing.
CineStream – Simple to use and offers a smooth, satisfying experience.
SmartFXPro – Clear platform, trading guides are easy to follow and understand.
focusforward – Clear message, focused action encourages measurable growth.
fashionhubonline – Smooth and user-friendly, exploring trends feels natural.
focusedgrowthsignals – Explains that focusing on signals helps maintain consistent and measurable growth.
focusedmotion – Good perspective, attention unlocks motion and accelerates project execution.
forwarddrive – Strong takeaway, moving forward requires taking action consistently.
3366utilitiesplus – Helpful insight, provides reliable tools that make processes simpler.
ElipsoCenter – Easy-to-navigate layout makes finding information straightforward.
DHPB-SmileHubOnline – Quick-loading pages with organized sections allow effortless navigation.
successportal – Useful observation, a reliable platform to navigate toward meaningful success.
??????????? ????? ??????????? ????? .
Mi ar?yorsunuz sekabet online casino? Sekabet Casino Türkiye’ye ula?mak ve kay?t, para yat?rma ve çekme konusunda kapsaml? bir rehberin yan? s?ra, sektördeki en iyi yaz?l?m geli?tiricilerinin sundu?u oyunlar? ve spor bahislerini ke?fetmek için villaperret26.com adresini ziyaret edin. Bonuslar?m?z ve promosyonlar?m?z cömert bir ödül program? sunar. Mobil uygulamam?z her yerde oynaman?za olanak tan?r – kullan?m? kolayd?r ve her cihaza indirilebilir.
ShineDeals – Attractive promotions are clearly displayed and browsing is simple.
LiveViewCams – Offers engaging live sessions that are easy to explore.
???????? Noblelift Equipment JSC Ltd. ??????????????? ???? ??? ??????? ????? ?? ???????????? ????????? ??????? ? ?????? ????????? ????? ???????????? ??? ????????????? ?????. ??????????? ???????????? ? ?????? https://nobleliftrussia.ru ?????????? ?????????????????, ?????????, ????????, ?????????????? ??????? ? ??????????? ?????? ? ????????? ?? ???? ???. ???????????? ????????????? ????????????? ?????????? EAC, CE ? ISO 9001, ???????????? ? ????? ??? ??? ????????????, ???????????? ??????????????? ?????????? ? ????????.
digitalfuturepath – Helpful resource, mapping your digital future is easier with structured advice.
ZBConnect – Users can explore sections easily with clear navigation paths.
??????? seo ??????????? ??????? seo ??????????? .
innovateandcreate – Inspiring hub, discovering great ideas leads to practical insights and productive outcomes.
forwardfocus – Strong message, direction sharpens motion and reduces wasted effort.
discoverqualitycontent – Useful takeaway, locating the right content saves time and improves workflow.
stylehaven – Relaxed and enjoyable, browsing collections is effortless.
clarityleadsway – Good perspective, progress with clear thinking produces consistent and meaningful results.
cangjiplatform – Good insight, the content is engaging and clearly organized for easy understanding.
A professional smile dental: therapy, surgery, orthopedics, and orthodontics all in one location. Individualized treatment plans, modern equipment, and strict sterility standards. We help you maintain long-lasting dental health.
UreyoPortal – Well-organized sections provide a seamless browsing experience.
mindcollaboration – Nice takeaway, connecting with top thinkers fuels innovation and teamwork.
confidentmoves – Helpful reminder, decisive actions drive steady growth forward.
ToolAccessOnline – Makes finding digital resources simple and fast.
WraoysPortalOnline – Smooth-loading pages with clear sections provide a pleasant user experience.
QuickHPWT – Offers multiple resources that are interesting and easy to access.
purposefuldrive – Practical guidance, purposeful drive ensures actions are intentional and results are meaningful.
focusedadvancement – Explains how focusing on what matters most drives sustained progress.
NowMiningHub – Organized mining resources make finding info fast and simple.
aarontguidehub – Very motivating, Aaront offers insights to take actionable steps for success.
claritydrivensteps – Useful thought, clarity in motion minimizes friction over time.
SmartFXLearning – Easy navigation, educational materials are practical and simple to follow.
businessalliances – Motivating and professional, emphasizes solid and lasting partnerships.
alignedmomentum – Helpful reminder, forward motion flows easily when clarity and goals match.
createyourlegacy – Valuable advice, inspires action to leave a personal and professional mark.
I need to share with you something most septic companies will not: there are two categories of people in this reality. Those who assume septic systems are simply “subterranean tanks for waste,” and those who have had raw sewage gurgling into their yard at midnight. I learned this difference the tough way in 2005—waist-deep in mud, trembling in a Washington rainstorm, as my family and I aided a weathered installer fix our family’s collapsed system. I was 14. My hands ached. My pants were wrecked. But that evening, something crystallized: This isn’t just manual labor. It’s people’s lives we are protecting.
Here’s the dirty truth: nearly all septic companies just maintain tanks. They are like quick-fix salesmen at a demolition convention. But Septic Solutions? They are unique. It all started back in the early 2000s when Art and his family—just kids hardly tall enough to carry a shovel—assisted install their family’s septic system alongside a grizzled pro. Picture this: three pre-teens waist-deep in Pennsylvania clay, understanding how soil porosity affects drainage while their buddies played Xbox. “We did not just dig holes,” Art explained to me last winter, warm coffee cup in hand. “We understood how ground whispers truths. A patch of marsh plants here? That’s Mother Nature yelling ‘high water table.'”
https://martinwuym708.tearosediner.net/the-link-between-septic-expertise-and-reduced-environmental-cleanup-costs
makeeverydaycount – Valuable point, strategies to maximize life help create meaningful experiences.
????????? ?????? http://dk-zio.ru/2025/12/solnechnye-batarei-chistaya-energiya-dlya-doma-i-biznesa/ .
AWSMiningDirectHub – Fast navigation with well-laid-out pages ensures information is accessible.
ViewPoint – Browsing feels smooth thanks to the organized design.
????????? ??????????? ???? seo-blog9.ru .
???? ??? ??????????? ?????? seo-blog8.ru .
ShopPacerPro – Exploring products is simple and visually appealing.
focusedmomentumgrowth – Demonstrates how focus and strategy keep forward motion efficient and impactful.
discoveryourstrengths – Strong insight, recognizing hidden strengths supports steady progress and personal growth.
signalpath – Strong point, attention aligns naturally when guided by signals.
communitygrowthhub – Helpful insight, community growth here encourages collaboration and shared achievements.
artesanoshubonline – Inspiring site, showcases artistic products from a cooperative of skilled artisans.
MiningCyrus – Users can quickly find mining-related resources in a practical interface.
XyadminCenter – Intuitive pages and clear layout enhance usability for basic operations.
attentionpowered – Good idea, focus transforms effort into motion.
??????? ????????? ?????? ??????
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
actionforge – Energetic, emphasizes shaping outcomes through deliberate effort.
purposefulmotion – Valuable point, purposeful steps provide direction and build momentum.
growstepbystep – Strong note, growth feels natural and achievable with the resources provided.
CortexLab AI https://cortexlab.app a 2025 guide to visual transformation tools: capabilities, use cases, limitations, and risks. We explain how to evaluate quality, ethics, and safety, select application scenarios, and work responsibly with AI.
successpathwayguide – Good observation, planning the steps helps maintain focus and achieve goals effectively.
IdeaCollection – A mix of resources keeps visitors curious.
AntsMarketPortalOnline – Clean interface and responsive pages enhance the shopping journey.
clarityoverbusyness – Explains that progress comes from focused work rather than endless tasks.
ShopMat – Items are well-presented, making browsing quick and enjoyable.
shareyourdreams – Motivating advice, expressing your dreams now brings support and valuable ideas.
bizgrowthcenter – Very practical, powerpres delivers business strategies that help boost efficiency daily.
GoogleRankSpot – The platform is user-friendly with ranking tools easy to navigate.
???????? ???????????? ???????????? ?????? ???????? ???????????? ???????????? ?????? .
alignedactions – Good observation, clarity aligns actions and strengthens progress.
clearpathfocus – Insightful note, concentrated focus influences motion and keeps tasks aligned.
ConnectForSuccess – Smooth navigation, collaborating with others is accessible and organized.
mindsparkshop – Energetic and thought-provoking, encourages exploring ideas in depth.
momentumpower – Useful note, focused effort generates forward motion and drives outcomes.
OuyicnNetworkHub – Organized interface and clear links provide effortless browsing.
???????? ?????????? ??? ????? ???????? ?? ?????? ?????
http://www.imxy28.com/space-uid-392705.html
onlinetoolspro – Useful observation, the toolbox simplifies tasks and helps users stay organized.
LinkManagerOnline – Makes organizing and accessing links simple.
networkandgrow – Great insight, online connections help you grow professionally and personally.
EasySoftOnline – Browsing software feels fast and practical.
HTechWebServiceNetworkHub – Well-arranged content and easy navigation improve overall user experience.
296wwtoday – Great resource, 296ww provides immediate access to useful tools for everyday needs.
?????? Apple ? ?????? rznonline.ru ? ?????????: ?????????, ????????, ????????, ???? ? ??????????. ?????????? ??????, ??????? ????, ????? ? ????????? ????? ???????. ????????? ??? ?????????? ???????? ? ??????? ?????.
iPhone 17 Pro Max cloudav.ru ? ???????: ??????? ?????, ??????? ????????????, ??????? ?????? ? ???????? ??????. ??????? ??????? ???????????? ??????, ???????? ??????????? ? ?????????? ??????? ????????. ???????? ? ????????? ????? ???????.
artvoyagehub – Inspiring platform, Art Voyage showcases creativity and artistic journeys worldwide.
https://allmynursejobs.com/author/mosbethu/
EscortDiamond18 – Navigation is smooth and finding sections feels effortless.
purposefocusedsteps – Clean takeaway, moving with intention today builds consistent progress.
??????????? ??????????? ?????? ?????? ??????????? ??????????? ?????? ?????? .
???? https://putana.biz/ — ??? ??????? ?????????? xxx ? ?????????? ??????????? ? ?????????? ??????????. ???? ??????? ??? ???????? ?????? ? ???????? ????????? ?????. ?????????? ???????????. ????????: ??????, ??????, ?????? ??? ????????, ??????? ??????????, ???????? ???????, ??????, ???? ? ????????. ????? ??????, ????? ?????, ????? ? ??????, ?????????? ??? ????????, ????? ??????, ??????? ????? ?????, ??????? ?????? ??? ??????? ???????????.
futurecraft – Inspiring and clear, ideas feel actionable and forward-looking.
??????????? ????????????? ?????? ?????????? ????? https://altai.travel/ – ??? ??? ???? ?????? ? ????????? ?? ??????? ????? ? ????? ?????, ? ????? ???? ??? ????? ???????????. ?????? ?????????? ????? ??? ??????????? ????, ? ????? ?????????? ? ?????????. ??????????? ???? ??????????? ? ??? ? ?????? ? ????? ???? ??????? ? ????!
claritycreatesroom – Insightful takeaway, direction opens space to think, prioritize, and execute.
mentalclaritydrive – Shows how taking proactive steps helps release mental pressure.
impactlaunchpad – Good note, initiating steps to create impact promotes progress effectively.
ideaexploration – Strong observation, exploring ideas deliberately opens new routes.
EscortOverview – Information is easy to understand and well arranged.
????????? ??????????? ???? seo-blog9.ru .
78YNetwork – Quick navigation and easy-to-find sections provide a smooth user experience.
2JasaHub – Users find a wide range of content with smooth browsing.
ShopAndShineNetworkHub – Well-laid-out pages and responsive design enhance product discovery.
brightfutureawaits – Motivating tip, your moment to shine brings clarity and direction for next steps.
basingstokepositivechange – Helpful platform, encourages local engagement for sustainability and environmental improvement.
? ???? ?????????????? ??????? ?????? “Individual Design” ? ?????? ?????????? ??? ????????? ??????? ?? ??????? ??????????? ???????, ????????? ?? ????????????? ?????? ?? ???????? ??????? ????????????? ? ?????????????? ???????-?????????? ?? LLumar, SunTek ? 3M. ????? ??????? ? ??????????? ?????? ?????????? ??????? ????? ? ???????????? ????????? ?? ????????? ????, ??????????? ?? ?????? ???????????? ????????????, ?? ? ???????? ?????? ?? ?????? ? ???????, ??? ???????? ????????? ? ??????? ?????????? ????????; ????????? ??? ?????????????? ?????? ????? ????????? ? ????????? ??? ??????, ?????? ?? ???????????? ???????????? ????????, ? ???? ??????? ???????? ????????? ? ???????? ??? ?????????? ????????. ???? ????? ??????? ????????? ? ?????????, ? ???? ????? ?? ???????? ??????, ????????? ?? https://individual-design.ru/ – ??? ????????? ?????, ???? ????? ? ?????? ??????, ??? ?????? ?????? ???????? ?????? ????????????? ???????.
KarsynConnect – Focused discussions are easy to find, and the platform feels welcoming.
cleanprocess – Helpful thought, a clean process starts with clarity and ends with results.
clean ecommerce hub – Smooth browsing experience shared, feels modern and organized.
move-forward-today – Leaves you ready to take action and achieve results without delay.
trendystreetwear – Fun and accessible, urban fashion looks easy to discover.
allthingsmarketing – Strong takeaway, covering all aspects of marketing in a clear and structured manner.
SuccessMindsetPro – Engaging site, resources are inspiring and easy to understand today.
????? 777 ??????????? ???? ????? 777 ???? – ??? ??????-????????????, ??? ??????????? ????? ? ???????????. ???????????? ???, ????????? ??????? ? ??????? ???????? – ??? ??? ??????? ?????????, ??????? ????? ???????? ???? ?????? ??????????? ??????. ????? ???????, ??? ??????, ?????? ?????, ???????? ????????, ? ??? ???? – ????????? ???????. ??????? ??????? ???????????? ? ?? ?????????? ?????? ????? ???? ??? ???????.
EasyMarlboro – The site design helps users explore quickly and efficiently.
SaltburnHubOnline – The site makes finding useful content fast and effortless.
iPhone 17 Pro Max https://giport.ru/sovet/technic-tips/phones-gadgets-tips/novye-funkczii-iphone-17-pro-max-chto-stoit-znat-o-programmnom-obespechenii-bezopasnosti-i-merah-zashhity-dannyh ??????????? ???????? ? ??????? ????????, ??????????? ??????? ? ??????? ????????? ??????. ???????? ????? ??? ?????????????, ??????? ????? ???????? ???? ? ?????, ???????? ? ??????? ? ?????????????.
?????? iPhone https://c-inform.info ??????? ????? ???????, ?????? ? ??????. ?????? ???????????? ??????? Apple, ????????, ?????????? ???? ? ?????????. ????????????, ??????? ?????? ? ??????? ???????? ? ??????? ?????.
Apple iPhone 17 Pro https://x-true.info/136496-iphone-17-pro-flagman-innovacij-v-mire-smartfonov.html ????????? ???????????? ? ???????????? ????????????. ?????? ???????, ??????? ???, ?????????? ?????? ? ?????????? ?????? ???????. ???????? ??? ?????? ????????, ??? ? ???????????? ?????.
growthwithpurpose – Nice observation, deliberate actions ensure growth stays on track.
general product shop – Straightforward store noted, selection felt practical.
ForexLearningHubPro – Clear and organized resources make understanding forex simple.
ManchunPortalOnline – Organized layout ensures users can reach information quickly.
team collaboration – A considered perspective that reflects the value of working together.
pokerok ??????? ??????? ??????????? ???? – ??? ???????? ???????? ?????????? ? ?????????, ?? ????????, ?????? ? ????????. ????? ????? ????? ?????? ?? ????? ???????, ?????????? ????, ?????????? ????? ? ?????? ???????. ??????????? ???? – ??? ???????? ???????????? ? ?????????, ??? ???????? ????? ? ???? ??????-?????????.
WZooAccess – Navigation feels natural and pages load without delay.
forwardcleanly – Shows that clean processes push work forward more effectively.
???? ? ??????? ? ????????? seo-blog8.ru .
progresspulse.click – Encouraging read, emphasizes momentum built through focused steps.
strategy-action-link – Helps bridge the gap between planning and successful execution.
melbet ??????????? Melbet ???? – ??? ??????? ? ?????????????? ????????? ??? ?????? ?? ????? ? ???? ? ??????. ?????????? ???????? ?????????, ??????? ???????? ??????? ? ??????? ????? ????? ?????? ????????????? ????? ??????????? ??????????. ?? ????? Melbet ????? ????? ??? ??????????? ??? ???????? ????: ??????????, ?????????? ??????, ?????????? ? ?????? ??????.
focuspath.click – Insightful content, demonstrates how concentrating effort drives consistent advancement.
inspirezone – Lively and motivating, makes discovering artful products enjoyable.
ideasurge.click – Useful post, emphasizes moving ideas forward daily.
QuickInfoHub – Information is easy to find and well organized for daily needs.
iPhone 17 Pro Max satom.ru ??????????? ???????? ? ??????? ????????, ?????? ??????????? ? ??????????? ????- ? ??????????????????. ???????? ????? ??? ?????????????, ??????? ????? ??????????????????, ???????? ? ????????????.
porno ???µ???µ??????
motionwithsignals – Practical insight, signals supporting motion make operations more effective.
CrowlLinkManager – Makes exploring and organizing resources quick and simple.
????? ???????????? ?????????? ??? ????: ??????????????, ????????????, ?????? ????, ?????? ???????????? ? ????????????. ???????? ?? ??????, ???????? ? ???????????, ????????? ????? ? ?????????????. ?????????? ?????, ????? ? ????????.
thrivedash product shop – Good navigation shared, overall shopping experience was smooth.
????? ??????? ?????? ??????? ????? ? ?????????? ???????????? ????????? ????????, ???????? ??????, ??????? ? ??????????? ??????? ????. ???????? ?????????? ? ?????????, ?????????????? ??? ?????? ????????. ???????? ????? ? ?????????? ??????.
clearintent – Shows how intent sharpens execution and outcomes.
forwardjourneyguide – Valuable advice, finding your way forward helps move steadily toward results.
BestDealCornerSpotOnline – Easy-to-follow design ensures offers are simple to browse.
PornsPortalOnline – Fast and responsive, minimal interface, content left unspecified.
Nomad Cars https://nomadcars.net/ — ??? ???????? ??????? ? ??????? ???? ?? ?????. ?????????? ?????????? ???????? ? ??????? ? ????????? ? ????? ????? ????! ?????????? ???????, ??????? ???? ? ?????? ????????????? ??????.
aligned partnerships – The message feels clear and applicable to working together.
growthanchor.click – Clear guidance, anchoring focus keeps momentum moving forward smoothly.
stepbystepforward.click – Encouraging and actionable, demonstrates how forward steps maintain momentum.
action-impact – Leaves you motivated to focus on actions that matter most.
TheFreeMathAccess – Well-organized content and responsive pages make math concepts easy to find.
forwardpower – Strong point, clear energy drives action and alignment.
styleinsights – Friendly and motivating, browsing fashion ideas feels natural.
????? ??? ?????????? ?????????? DreamStalker Expert ?????????? ????????? ?? ??????????? ????????????? ???????? Wi-Fi ???????????, ????? ????????? ???????? ????, RGB-???????????? ? OLED-????????. ?????????? ???????? ?? https://claps.me/catalog/pribory-dlya-osoznannykh-snov/pribor-dlya-osoznannykh-snovideniy-dreamstalker-expert/ ? ??????? ????????? ? ????????? ?????-?????? ? ???????????????? ?????????? tACS. ??????? ???????????? ?????????? ????, ???????? ???????????? ? ????? ???????????? ???????????? ?????????? ???????????.
progressengine.click – Concise guidance, helps understand and implement strategies effectively.
focuspulse.click – Insightful read, demonstrates how maintaining focus accelerates results.
ebony porn
I need to tell you something nearly all septic companies refuse to: there are two categories of people in this world. Those who think septic systems are merely “underground boxes for waste,” and those who’ve had raw sewage gurgling into their property at 2 AM. I discovered this difference the hard way in 2005—waist-deep in mud, trembling in a Washington rainstorm, as my siblings and I aided a weathered installer restore our family’s collapsed system. I was 14. My hands blistered. My pants were wrecked. But that moment, something changed: This ain’t just manual labor. It’s folks’ lives that we’re preserving.
Let me share the dirty truth: nearly all septic companies just pump tanks. They’re like temporary salesmen at a chainsaw convention. But Septic Solutions? They’re special. It all began back in the early 2000s when Art and his siblings—just kids hardly tall enough to carry a shovel—aided install their family’s septic system alongside a experienced pro. Picture this: three youngsters waist-deep in Pennsylvania clay, understanding how soil porosity affects drainage while their friends played Xbox. “We never just dig trenches,” Art shared with me last winter, warm coffee cup in hand. “We learned how soil whispers secrets. A patch of marsh plants here? That’s Mother Nature shouting ‘high water table.'”
https://www.hotfrog.com/company/1065626b054c66955e8fec3a6478b047/septic-solutions-llc/arlington/cleaning-services
SmokeEssentials – A useful site where browsing feels natural and relaxed.
Allow me to share with you something most septic companies won’t: there are two kinds of people in this life. Those who assume septic systems are simply “buried containers for waste,” and those who’ve had raw sewage bubbling into their yard at 2 AM. I discovered this difference the tough way in 2005—waist-deep in muck, shivering in a Washington deluge, as my siblings and I helped a weathered installer repair our family’s broken system. I was 14. My hands blistered. My clothes were destroyed. But that evening, something clicked: This isn’t just manual labor. It’s families’ lives we’re protecting.
Here’s the harsh truth: nearly all septic companies just maintain tanks. They are like band-aid salesmen at a disaster convention. But Septic Solutions? They are unique. It all originated back in the beginning of the 2000s when Art and his brothers—just kids barely tall enough to carry a shovel—assisted install their family’s septic system alongside a weathered pro. Visualize this: three youngsters buried in Pennsylvania clay, discovering how soil absorption affects drainage while their buddies played Xbox. “We never just dig holes,” Art shared with me last winter, steaming coffee cup in hand. “We understood how ground whispers mysteries. A patch of wetland vegetation here? That’s Mother Nature shouting ‘high water table.'”
https://charlierolt530.trexgame.net/what-makes-septic-certification-a-trust-signal-for-homeowners
vs
trust and community network – Encouraging platform shared, feels uplifting and team-oriented.
??????????? ??????????? ?????? ??? ????????? ??????: ?????????????? ??????, ??????? ?????, ????? ??????? ? ??????. ?????????? ??????????????, ?????????, ??? ? ??????????? apres-ski. ????????? ????? ??? ??????? ???????.
????? ?????? ? ????? ??????? ? ?????? ?????? SEO-???????????, ??????????? ?????? ? ??????? ? ?????? ??????: ???????? ??????? ?????? ? ??????. ?????, ?????????, ???????, ??????????? SEO, ????????? ? ??????? ???????. ???????? ?? ????????? — ???? ?????, ?????? ? ???????.
porno chinese
clarityleads – Explains how clarity in priorities ensures activities deliver real results.
organizedpath – Demonstrates that organizing the path ensures tasks lead to tangible outcomes.
digital ????????? ???? digital ????????? ???? .
NextLevelTradingNetworkHub – Logical structure and neat pages improve user understanding.
??????????? ????? ? ??? ?? ??????? prodvizhenie-sajta-po-trafiku1.ru .
tractionguide.click – Encouraging and actionable, shows how to build forward movement effectively.
SeoBomba.ru — ?????? ??????????? ?????? ????? ?????? ??????, ???????? ??????????, ?????????? ??????? ? ???????? ??????? ? ????????? ???????? ? ???????? ?? ????????? ? ???????????? ????????. ??????? ???????? ??????? ??????????? ?????, ??????? ?????????? ??????? ? ???????????????? ?????? ? ??????? ???????. ???????????? ? ???????, ???????? ? ???????? ??????????? ????? ?? https://seobomba.ru/ — ????????? ???????? ??? ??? ????????-?????????, ??? ? ??? ?????????????? ??????, ??? ????? ????????? ? ?????? ?? ???????????? ??????.
immediate-implementation – Shows how to act on ideas without delay.
kickoffideas.shop – Short but inspiring, emphasizes taking action.
trendscout – Energetic and helpful, trends feel easy to track.
pathwayclarity.click – Simple and effective, makes understanding motion easier.
????? ??????????? ???? ????? – ??? ???, ???? ???????????? ? ??????????? ????????? ????, ?????? ??????? ??? ??????. ?? ??????? ????????? ?????????? ????? ??? ???????? ???????????, ????????? ?????????? ?????????? ? ????????????? ??????. ??????, ????? ???????, ??? ?? ?????? ????????? ?????????? ??????????, ????????? ??????????? ??????? ? ???????? ??????.
???????? ? ?????? ?? ????? ???????? ?? ????? ? ?????? ??? ???????????
leadership growth network – Solid reference shared, promotes meaningful support and learning.
directioncorner.click – Clear guidance, helps me create actionable steps toward growth.
ForexSelectLive – Well-laid-out platform ensures traders can find data quickly.
digital ????????? ???? seo-blog9.ru .
dailyinspirationhub – Motivating content, finding inspiration daily helps stay energized and creative.
<momentumfromstrategy – Shows how applying strategy as energy ensures ongoing actionable success.
????? ??????? ?????? ????????: ????? ?? ???-???????????, live-??????, ??????? ? ?????. ????????? ??????? ???????, ???????, ???????? ? ????? ???????, ?????????? ? ???????????. ?????????? ??? ???????? ???????.
focusflow.click – Inspiring ideas, anchoring attention leads to tangible growth.
clarityengine.click – Simple insight, emphasizes how organized thinking strengthens results.
growth-direction – Helps stay on course with a clear path forward.
designessentials.shop – Useful and practical, highlights key design basics.
actionhub.click – Concise tips, encourages regular action for consistent forward movement.
winmore online marketplace – Good browsing experience shared, offerings feel trustworthy.
steadfastcircle – Very solid, evokes a sense of unwavering support.
shapedirection.click – Clear and actionable, emphasizes how thoughtful direction enhances results.
porno music
Post34Network – Smooth browsing and clear navigation make the site user-friendly.
actionengine – Demonstrates how focused effort powers forward movement and results.
creativecorner.click – Practical advice, shows how imagination fuels forward action.
fastsolutionguide – Insightful perspective, fast solutions prevent delays and support smooth operations.
actnowoverhesitate – Highlights that immediate action often produces better results than delaying.
design-focus-growth – Inspires focused action that leverages design for results.
porno sait
idea discovery space – Fresh site shared, supports regular creative thinking.
clarityenginehub.click – Straightforward guidance, illustrates how clarity accelerates movement and performance.
connection driven – Simple but effective comment about relationship-first thinking.
action clarity – Practical ideas that turn direction into measurable progress.
????? ??????? ?????? ??? ????????, ???????, ?????????? ???????? https://victoryhome.ru/ – ??? ?????? ????, ? ??? ??? ? ???????, ????, ???????, ?????, ?????, ?????????, ??????????, ????, ???????? ? ?????? ??????. ?????? ? ????? ?????????? ?????????, ??? ???????? ??? ???????? ?????????? ?????????? ?????? ????. ????????? ?? ?????.
best premium porn site
????????? seo ???? seo-blog8.ru .
?????? ?????? https://kushslots.ru: ????? ?? ?????????? ???????????, live-??????, ????? ? ???????. ????????? ???????? ????????, ???????, ??????? ? ????? ??????, ?????????? ? ???????????. ???????? ????? ?????????????? ????????.
?????? ?????? https://catcasino-origin.ru ?????, live-?????? ? ??????????? ???????????. ???????? ? ???????????, ???????, ?????? ??????? ? ???????????? ????????. ????? ??????? ???? ??????????? ??????? ???????.
movementlogic.click – Clear guidance, makes taking consistent action feel achievable.
collaboration partner store – Useful platform reference, items seem suited for long-term use.
Forward Compass – Informative content, shows how clear focus accelerates progress.
anchorsteps.click – Informative read, emphasizes taking deliberate action.
progresspath.click – Very informative, emphasizes that clear forward steps produce real results.
achieve-more – Encourages turning potential into tangible accomplishments.
Allow me to share with you something the majority of septic companies won’t: there are two types of people in this world. Those who assume septic systems are merely “subterranean tanks for waste,” and those that have had raw sewage erupting into their backyard at 2 AM. I understood this reality the tough way in 2005—knee-deep in sludge, shivering in a Washington downpour, as my siblings and I helped a weathered installer restore our family’s broken system. I was a teenager. My hands were raw. My jeans were ruined. But that evening, something changed: This is not just digging. It’s families’ lives that we’re protecting.
Let me share the dirty truth: most septic companies just maintain tanks. They are like band-aid salesmen at a disaster convention. But Septic Solutions? These guys are different. It all started back in the beginning of the 2000s when Art and his family—just kids hardly tall enough to lift a shovel—helped install their family’s septic system alongside a experienced pro. Imagine this: three kids knee-deep in Pennsylvania clay, understanding how soil permeability affects drainage while their buddies played Xbox. “We didn’t just dig holes,” Art explained to me last winter, steaming coffee cup in hand. “We discovered how soil whispers truths. A patch of wetland vegetation here? That’s Mother Nature screaming ‘high water table.'”
https://www.pinterest.com/pin/624241198844572503/
directionmomentum.click – Clear advice, shows how maintaining direction powers progress over time.
action guide – Helpful breakdown of how direction improves effectiveness.
Forward Pathway – Clear advice, demonstrates simple techniques to achieve steady progress.
visibilityenhancer – Good point, maintaining a strong online presence boosts influence and recognition.
digital shopfront – Nicely laid out with a collection that feels curated.
fresh porno
Clarity Path – Very motivating advice, makes creating and following purposeful steps easy.
Concept Flow – Helpful guidance, makes executing new ideas feel simple and achievable.
Flow Alignment – Clear advice, ensures actions are structured and results-oriented.
trans porn
business growth solutions – Relevant recommendation, appears solution-driven.
porno ?¶?µ???‚????
Idea Accelerator – Informative content, really useful for maintaining forward motion on projects.
pathwaypulse.click – Encouraging perspective, highlights how guidance keeps daily progress clear and achievable.
Forward Flow – Helpful insights, makes understanding momentum in action simple.
?????? ??? ?????????? ?????????? DreamStalker Expert ?????????? ????????? ???????????? ????? ????????????? ????? ? ??????????? ?? Wi-Fi, ????? ????????? ???????? ???? ? RGB-????????????. ????? ??????????? ??????? ???????? DreamStalker? ?laps.me/catalog/pribory-dlya-osoznannykh-snov/pribor-dlya-osoznannykh-snovideniy-dreamstalker-expert/ ?????????? ?????????? ? ??????????? ????????? ?????-?????? ? ???????????????? ?????????? tACS, ?????????????? ??????? ?????????? ? ?????????? ???????????. ??????? ???????? ? ??????? ???????????? ? ?????? ???????????? ???????????? ?????????? ???????????.
snuff porno
signalflowhub.click – Clear and encouraging, shows how signals help sustain progress over time.
idea-to-step – Encourages taking ideas and creating realistic, achievable actions.
??????? ??????? ????? ? ?????? – ??????-??? https://www.martin-sad.ru/ – ??? ????????-??????? ????????? ????????. ???????????? ?? ????? ? ????? ?????? ? ??????? ????????? ???????? ? ????????, ? ????? ???????? ??? ????. ? ??? ???? ????? ??????? ?? ????? 2026 ?? ???????? ?????. ? ??? ???? ??????: ??????? ????????, ???? ?? ????????, ???????? ????????, ??????????? ??????.
productivityunlock.click – Insightful content, it’s helped me organize my work more efficiently and stay focused.
progresspulse.click – Easy-to-follow suggestions, emphasizes aligning actions with clear direction.
clarityactivatesgrowth.click – Helpful insights, the clarity in each post really helps me direct my focus on key tasks.
???? ? ??????? ? ????????? seo-blog12.ru .
Idea Momentum – Useful tips, demonstrates how ideas can drive action effectively.
Action Blueprint – Clear advice, shows actionable ways to align focus with meaningful results.
????????? ?????? ???????? prodvizhenie-sajta-po-trafiku1.ru .
Let me share with you something nearly all septic companies will not: there are two kinds of people in this life. Those who think septic systems are merely “underground boxes for waste,” and those who’ve had raw sewage bubbling into their backyard at the dead of night. I discovered this difference the tough way in 2005—knee-deep in sludge, trembling in a Washington downpour, as my family and I helped a grizzled installer restore our family’s broken system. I was 14. My hands were raw. My clothes were ruined. But that night, something crystallized: This ain’t just manual labor. It’s families’ lives that we’re preserving.
Here’s the ugly truth: nearly all septic companies just service tanks. They act like quick-fix salesmen at a disaster convention. But Septic Solutions? They are different. It all began back in the beginning of the 2000s when Art and his siblings—just kids scarcely tall enough to lift a shovel—assisted install their family’s septic system alongside a grizzled pro. Picture this: three pre-teens knee-deep in Pennsylvania clay, discovering how soil absorption affects drainage while their friends played Xbox. “We did not just dig holes,” Art told me last winter, steaming coffee cup in hand. “We discovered how ground whispers truths. A patch of marsh plants here? That’s Mother Nature yelling ‘high water table.'”
https://www.flickr.com/people/203909751@N04/
teamunity.shop – Helpful perspective, shows how collaboration is strengthened by trust.
collaborative ideas center – Well-rounded site shared, supports open creative exchange.
seo ? ??????? ???? seo-blog9.ru .
Purposeful Ideas – Very practical posts, makes turning ideas into actions simpler today.
Momentum Path – Really helpful guidance, makes following daily actions much easier.
Momentum Path – Clear explanation, shows how taking action builds meaningful progress.
Forward Path – Very insightful, provides simple steps to keep momentum going consistently.
focuscorner.click – Encouraging read, emphasizes building growth through deliberate attention.
motionengine.click – Clear and motivating, demonstrates how focused effort keeps projects advancing.
purposeful-path – Inspires moving forward with intention and clarity.
ideas-forward.click – Inspiring advice, helps translate concepts into real-world action.
clarityactivatesgrowth.click – I love how organized the posts are, very easy to focus on the key steps.
clarityenablesmovement.click – Great insights here, clarity really makes understanding and acting much easier.
Focus Tracker – Helpful suggestions, shows how to stay on the right track.
???????? ?? ??????, ? ?????? ????, ????????????? ???????? “??? ????”, ? ??????? ???????? ???????? ???????? ? ???????????? ????????, ?????????? ?????????? ??? ???????????? ???????. ? ???????????? ??????? ??????, ?????, ?????, ?????, ???? ????????? ????????????? ??????? ? ???????????? ????, ??? ?????????? ? ??????? ? ????????? ???????? ??????. ???????? ??????? ? ??????: ??????, ?????????, ????????, ?????????, ??????? ???????????? ?????????, ????, ??????? ? ?????, ????? 500 ??????? ?? ??????????? ??????????? ?? ??????. ??????? ??????????? ????????????? ????????????, ?????? ?? ???????? ? ???????, ??????????? ???????? ???????? ?? ????????? ?????. ???????? https://sadovodklin.ru/ ????? ???????????? ? ?????????, ??????? ? ???????, ??? ??????? ???????? ?? ????? ?? ????? ? ??????? ???????? ?????? ??????, ? ???????? ????? ????? ?????? ??? ?? ???????? ??? ??????????.
xxxl porno
Forward Growth – Very practical guidance, makes staying focused and moving ahead simpler.
azino 777 ????? 777 – ??? ???, ??????? ????????? ??? ?????? ????????? ???????? ??? ? ????. ??? ????????, ???????? ????? ?????????? ???????, ?????????? ???? ? ??????-???????????? ??????. ???????? ?? ?????????????? ?????????, ????????? ?????????? ?????????? ???????? ??????? ????? ??????? ???????? ? ?????????? ??????? ?????????. ?? ??????? ????????? ?????????? ??????? ???????, ????????? ????????????? ??????? ? ??????????? ???????.
Direction Navigator – Very clear content, makes planning and executing tasks faster.
Focused Concepts – Practical advice, makes approaching projects with precision easier.
mental clarity – Quick to go through, but it leaves a lasting impression.
Idea Clarity – Very practical posts, simplifies turning thoughts into action steps.
Focus Guide – Practical advice, helps maintain direction while moving forward.
clarityflow.click – Clear perspective, highlights how clarity channels energy efficiently.
results-focused-strategy – Shows how structured focus leads to repeatable success.
energizedmotion.click – Practical suggestions, gives tips to stay productive while moving forward.
progressmovesbyclarity.click – Excellent advice, it helps me break things down and keep moving toward my goals.
porno iznasilovanie
ideastart.click – Clear guidance, motivates quick action on inspiring concepts.
?????? ???? yawanawa
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
Signal Compass – Engaging advice, highlights how guided growth strategies produce results.
Momentum Signals – Very clear content, shows how using signals drives consistent progress.
Innovation Map – Clear guidance, shows ways to structure ideas for better results.
?????? ????? ????? Xiaomi, Viomi, Mijia. ????????? Wi-Fi, ???????? ???????, ?????? ????????.?????? ?????????? ????? Hisense ?????? ?????? ???????????? ??????? Maunfeld. ?????????????? ???? ??????????, ?????? ?????? ????, ?????? ??????? ?????. ?? ???????????? ?????????? ????????? ? ???????????? ???????. ????????? ???? ?? ????????. ?????? ?????????? ????? Korting ??????
????? ???? ????? – ??? ???, ???? ???????????? ? ??????????? ????????? ????, ?????? ??????? ??? ??????. ?? ??????? ????????? ?????????? ????? ??? ???????? ???????????, ????????? ?????????? ?????????? ? ????????????? ??????. ??????, ????? ???????, ??? ?? ?????? ????????? ?????????? ??????????, ????????? ??????????? ??????? ? ???????? ??????.
porno rule
Focus Flow – Easy-to-read articles, provides clear direction for daily tasks.
????? ??? ???????? ???????? ?????? ?? ?????? ????????? xn--rdacteurmmoire-bkbi.com ?????????? ???????????????? ?????? ?? ????????? ????????????? ?????: ???????? (TFE), ???????????? ???????????, ?????????? ??? ? ???????? VAE ?? 18 ???? ?? ????????. ????????? ??????? ???????????? ???????????? ???????????? ?????????? ??? ?????????????, ?????????????? ?????????? ? ????????? ??????????? ?????? ? ?????????? ??????????. ?????? ???????? ? ?????????? ???????????? — ?? ???????? ?? ?????????????, ????????? ?????? ????? ?????????? ?? 24 ????? ?? ???? ? ???????????? ????????????? ? ?????????????? ??????????.
Growth Map – Useful tips, really supports organizing goals and growth actions.
steadyclimb.click – Simple advice, inspires moving forward one step at a time.
Action Engine – Clear and practical, shows how momentum builds from sustained focus.
Action Accelerator – Enjoyed the posts, very clear guidance for moving projects forward rapidly.
drivemomentum.click – Uplifting advice, links ongoing effort to visible success.
clarityflow.click – Easy-to-follow advice, shows how clear thinking powers faster progress.
???? ????????? ????????-?????????? seo-blog8.ru .
clarityturnsprogress.click – Great tips, really helps me turn progress into something achievable every day.
rule porno
execution guide – Solid examples of how focus strengthens performance.
where internet partner prodvizhenie-sajta-po-trafiku3.ru .
forwardhub.click – Clear strategies, practical steps that can be applied immediately.
Clarity Keys – Clear tips, helps organize tasks so they are easier to execute.
clarity-flow.click – Inspiring content, makes understanding complex ideas much easier.
Flow Compass – Clear and practical, keeps progress moving without distractions.
?????? ????????? 2026 ????????? ????????????? ????????? – ??? ???????? ??????????? ??? ?????????? ???????????????? ??????? ????????? ????? ? ?????????????? ???? ????????. ?????????? ?????????? ??????????? ? ???????, ??????????????? ??????? ?????????? ? ???????? ? ???????. ?????? ??? ????? ????????? ? ????????????? ???????, ? ????? ??? ????????? ???????????? ???????????, ?????????? ???????????????? ??????? ?????????.
???? ??? ??????????? ?????? ???? ??? ??????????? ?????? .
Path Clarity – Easy-to-follow content, gives practical methods for moving forward smoothly.
Action Path – Helpful insights, very clear and structured content for smooth progress.
kz porno
fresh perspective – The way this was explained helped shift how I view my goals.
progressforward.click – Clear and simple, demonstrates how moving confidently creates momentum.
makan buffet ????? ?????? ??? ????????? ?? ????? ???????
freeze porno
forwardgrowthengine.click – The content here makes it so much easier to push growth in the right direction.
Allow me to tell you something most septic companies will not: there are two categories of people in this world. Those who assume septic systems are merely “buried containers for waste,” and those who’ve had raw sewage gurgling into their property at 2 AM. I discovered this reality the hard way in 2005—standing in sludge, trembling in a Washington rainstorm, as my siblings and I aided a veteran installer restore our family’s failed system. I was fourteen. My hands blistered. My clothes were ruined. But that moment, something crystallized: This ain’t just manual labor. It’s people’s lives we are protecting.
Here’s the harsh truth: most septic companies just pump tanks. They are like temporary salesmen at a chainsaw convention. But Septic Solutions? They’re unique. It all started back in the early 2000s when Art and his brothers—just kids scarcely tall enough to lift a shovel—helped install their family’s septic system alongside a experienced pro. Picture this: three pre-teens buried in Pennsylvania clay, discovering how soil absorption affects drainage while their peers played Xbox. “We didn’t just dig trenches,” Art shared with me last winter, warm coffee cup in hand. “We learned how soil whispers secrets. A patch of marsh plants here? That’s Mother Nature yelling ‘high water table.'”
https://gitee.com/marketing_dd9a
a href=”https://forwardmomentumforms.click/” />helpful resource – Practical thoughts on keeping momentum moving consistently.
productivityengine.click – Excellent advice, helps boost my productivity and speeds up my daily tasks.
porno stockings
Progress Engine – Helpful content, shows ways to turn goals into structured action.
I need to tell you something nearly all septic companies will not: there are two types of people in this world. Those who believe septic systems are simply “subterranean tanks for waste,” and those who’ve had raw sewage gurgling into their backyard at the dead of night. I understood this difference the difficult way in 2005—standing in mud, shivering in a Washington deluge, as my family and I aided a veteran installer fix our family’s failed system. I was fourteen. My hands blistered. My clothes were ruined. But that moment, something clicked: This isn’t just manual labor. It’s families’ lives we are safeguarding.
Here’s the harsh truth: nearly all septic companies just maintain tanks. They act like band-aid salesmen at a demolition convention. But Septic Solutions? They’re unique. It all started back in the beginning of the 2000s when Art and his siblings—just kids scarcely tall enough to lift a shovel—assisted install their family’s septic system alongside a grizzled pro. Picture this: three kids waist-deep in Pennsylvania clay, understanding how soil absorption affects drainage while their buddies played Xbox. “We didn’t just dig ditches,” Art explained to me last winter, hot coffee cup in hand. “We discovered how earth whispers mysteries. A patch of cattails here? That’s Mother Nature shouting ‘high water table.'”
https://atavi.com/share/xmfw1ezwj7nx
forwardfocus.click – Practical advice, highlights the role of focused action in creating opportunities.
??????? ?? ??????? ???? ?????? ??????, ???????????? ????, ???????? ??????? ? ?????? ?? ?????? ??????? ?????????? https://kruizy-po-persidskomu-zalivu.ru/
?????? ?????? https://kometa-casino-online.ru ?????? ?????? ? ????? ? live-??????. ?????? ???????????, ???????, ?????? ????, ??????? ? ???????? ?????? ???????.
???????? «?????? ??????» ?????????? ??????? ??????? ??????? ??????????? ???????????? ????????? ???????? ?? ???????? ?????. ????? ???????????? ?? ?????????? ???????????, ???????????? ? ??????? ?????????, ?????????????? ???????, ????????? ???? ? ???????? ????????. ????????? ????????? ?????? ?? ????? mr-parquet.ru ???????????? ????????? ??????? ?????????????? ? ?????????? ?????????? ? ????????????. ?????????? ???????? ???????????????? ????????????, ?????? ??????? ? ???????? ?? ??????. ?????????? ?????????? ? ?????? ???????????? ??????? ????????? ?? ??????? ?????????????? ??????????.
Clean Progress – Very clear and practical, makes planning steps simple and effective.
Guided Action – Helpful advice, helps me stay concentrated on what truly matters.
Progress Compass – Helpful insights, explains the connection between clarity and consistent forward motion.
?????????? ??????????? seo prodvizhenie-sajta-po-trafiku1.ru .
Hello! Do you use Twitter? I’d like to follow you if that would be okay. I’m definitely enjoying your blog and look forward to new updates.
???? ????? ??????
focusbuildspathways.click – Very clear advice, helps me stay organized and focused on what matters each day.
signalsmatter.click – Concise and motivating, emphasizes the importance of acting on cues.
results guide – Easy-to-follow ideas showing how focus improves outcomes.
????? ???? ?????? ????? – ??? ????????? ??????????, ??? ????? ?? ??????? ?????? ????, ??? ????? ?? ????????. ?? ?????? ???? ???? ??????? ???? ??????? ? ?????. ??????? – ?????? ????????????, ?? ????? ?? ??? ????????? ?????? ? ?? ??????? ? ???, ??? ? ????? ???? ??????? ?????? ?????? ? ?????????? ?????.
porno pussy
Focus Path – Insightful tips, helps organize tasks for maximum personal improvement.
Just want to say your article is as amazing. The clearness in your post is just spectacular and i can assume you are an expert on this subject. Well with your permission let me to grab your RSS feed to keep up to date with forthcoming post. Thanks a million and please carry on the rewarding work.
??????????? ???? ??????
thailand porno
focusedimpact – Demonstrates that concentrated focus enhances the impact of executed actions.
Directed Focus – Helpful articles, content gives practical steps for staying on track.
focus-on-growth.click – Clear strategies, channeling direction maximizes growth potential.
??????? ????? ?? ????? ??????? ?????
Growth Flow – Informative content, makes developing processes more approachable and efficient.
Momentum Engine – Useful tips, explains how focus fuels steady advancement.
growthfollowsdesign.click – Clear and actionable steps, makes organizing my tasks and plans much easier.
Forward Focus – Helpful advice, posts make it easier to stay organized and productive.
forwardtractionformed.click – Simple yet powerful posts, makes it easy to maintain focus and move forward.
??????????? ?????? ?? ??????? ??????????? ?????? ?? ??????? .
visit this site – Helpful guidance on bringing thoughts and execution into sync.
MomentumMap.io – Layout communicates direction and clarity, making progress easy to visualize.
clarity creates momentum – Reinforces a strong link between focus and steady progress.
Easy Flow – Very motivating advice, explains how removing friction speeds up progress.
Action Pathway – Very clear guidance, makes executing daily plans much easier.
Progress Pathway – Very practical, explains how structured steps create consistent forward movement.
Stepwise Motion – Helpful insights, structured in a way that clarifies each step.
growthfollowsdesign.click – Very useful advice, helps me stay on track and organize my plans better each day.
???????????? ?????????? ????????????? plazm-sterilizatory.ru .
??????????? ???????????? ? ??????? http://financeprofessional.ee/ .
Clarity Moves – Very useful, posts make acting on plans feel straightforward and efficient.
Easy Momentum – Clear and actionable tips, really simplifies moving projects forward.
claritydrivesmovement.click – Informative articles, helps break down tasks into manageable steps with less stress.
recommended site – Straightforward explanation of how direction drives better results.
GrowthNavigator.io – Layout feels minimal but effectively highlights the forward-thinking theme.
?? ????? ?? ?????? ????? ?????? ?????
Signal Pulse – Practical examples, shows how small signals can trigger meaningful forward motion.
porno club
Momentum Map – Very practical, helps maintain steady movement toward goals.
Progress Compass – Very useful, helps organize efforts for maximum forward movement.
speed through focus – Communicates a tight message that inspires confident forward motion.
Project Momentum – Posts are clear, making planning and action much easier.
focusfeedsmomentum.click – The posts are clear and actionable, making it easy to make real progress.
Allow me to share with you something nearly all septic companies will not: there are two categories of people in this world. Those who believe septic systems are simply “buried containers for waste,” and those who have had raw sewage gurgling into their property at 2 AM. I understood this distinction the difficult way in 2005—knee-deep in muck, trembling in a Washington downpour, as my brothers and I helped a weathered installer restore our family’s failed system. I was 14. My hands were raw. My clothes were destroyed. But that night, something crystallized: This ain’t just manual labor. It’s families’ lives we are preserving.
Here’s the harsh truth: most septic companies just maintain tanks. They are like band-aid salesmen at a disaster convention. But Septic Solutions? They are special. It all started back in the early 2000s when Art and his brothers—just kids scarcely tall enough to lift a shovel—helped install their family’s septic system alongside a experienced pro. Imagine this: three youngsters waist-deep in Pennsylvania clay, learning how soil porosity affects drainage while their buddies played Xbox. “We didn’t just dig ditches,” Art shared with me last winter, hot coffee cup in hand. “We discovered how soil whispers secrets. A patch of marsh plants here? That’s Mother Nature screaming ‘high water table.'”
https://www.spreaker.com/podcast/aebbatmhhx–6835263
focuschannelsenergy.click – The content is structured so well, it’s easy to start applying immediately.
clarity tools – Useful reminders that make focusing feel less overwhelming.
seo ???? seo ???? .
Guided Focus – Helpful posts, offers actionable ideas for daily productivity.
clarity-in-motion.click – Very practical, helps ensure every step moves toward desired outcomes.
ForwardNavigator.net – Presentation is smooth, directional concept comes through naturally.
??????????? ??????????? ?????? ??? ??????? ???????: ?????????????? ??????, ??????? ?????, ????? ??????? ? ???????? ??????????????. ?????????? ?????, ????????? ? ??????????? apres-ski ??? ???? ?????.
porno scat
focuspillar – Practical advice, keeps me organized and on point with my tasks.
??????-????????? https://rosseriaall.net/ ?????????? ?????????? ???????? ?????????? ???????? ? ??????? ???????? ??? ???????????. ???? ???????? ????????????????? ?????, ??????????? ?????????????, ????????, ??????? ????????, ?????????? ? ?????????? ???????, ?????????????? ? ???????? ??????? ? ??????? ?????????? ?? ?????????? ? ???????? ???????. ???????? ??? ???????????? ??????? ??????? ???, ??? ? ??????? 2025 ????. ?????????? ?????????? ?????????? ? ??????? ??????? ?????? ???? ??????????? ????????? ?????????? ?????? ?????? ? ????????? ??? ?????????????.
Clarity Compass – Useful content, simplifies understanding and applying growth techniques.
??? ???? ????? ????????? ?????? ??????????? prodvizhenie-sajta-po-trafiku1.ru .
brazil porno
ideasbuildmomentum.click – Great tips, helps me stay focused and organized while making steady progress on projects.
Idea Flow – Practical insights, reminds that ideas move forward best when they have a clear path.
clarity based progress – The idea feels intentional and easy to follow.
GrowthPathway.io – Text emphasizes clear steps, direction and growth feel aligned.
clarityguidesdirection.click – Straightforward and motivating, helps set clear goals and make steady progress.
https://evakuatorhelp.ru/ ???? ???????? – ??? ????????????? ? ??????????? ?????? ??????, ??????? ??????? ? ????????? ???????? ??? ?????????? ?? ????????? ??????????, ??????????? ??? ??????? ? ???????? ?? ?????????? ?????? ? ??????? ? ???????????. ?? ??????????? ?????????? ???? ??? ???????????? ??? ???????????????, ????? ????????? ??????????? ???????????. ?? ????????? ???????? ???????????? ????? ???????????, ????? ??? ????? ?????????? ?????? ????? ??????, ????????? ? ?????????? ??????????.
Energy Flow – Practical advice, makes following through on plans feel simpler.
Recommended reading: https://xn--80aajombyba1db9b5c.xn--p1ai/instillyaczii-mochevogo-puzyrya-effektivnyj-metod-lecheniya-czistita-u-zhenshhin/
ClarityInMotion.net – Layout emphasizes forward movement, making progress easy to follow.
ClearPathForward.com – Concept is easy to grasp, direction and focus are very apparent.
I need to tell you something most septic companies will not: there are two kinds of people in this world. Those who assume septic systems are simply “subterranean tanks for waste,” and those who’ve had raw sewage bubbling into their property at midnight. I learned this reality the tough way in 2005—waist-deep in sludge, freezing in a Washington deluge, as my family and I helped a veteran installer restore our family’s failed system. I was a teenager. My hands blistered. My jeans were destroyed. But that moment, something clicked: This is not just manual labor. It’s families’ lives we are preserving.
Let me share the ugly truth: nearly all septic companies just maintain tanks. They are like band-aid salesmen at a disaster convention. But Septic Solutions? They are unique. It all began back in the beginning of the 2000s when Art and his brothers—just kids hardly tall enough to lift a shovel—assisted install their family’s septic system alongside a grizzled pro. Picture this: three pre-teens waist-deep in Pennsylvania clay, understanding how soil absorption affects drainage while their buddies played Xbox. “We did not just dig ditches,” Art shared with me last winter, warm coffee cup in hand. “We discovered how earth whispers mysteries. A patch of wetland vegetation here? That’s Mother Nature shouting ‘high water table.'”
https://about.me/septicsolutionsllc
GoalDrivenFocus – Very actionable, ensures I meet weekly targets with less effort.
? ???? ?????????????? ??????? ?????? “Individual Design” ? ?????? ?????????? ??? ????????? ??????? ?? ??????? ??????????? ???????, ????????? ?? ????????????? ?????? ?? ???????? ??????? ????????????? ? ?????????????? ???????-?????????? ?? LLumar, SunTek ? 3M. ? ???? ?????? ??????? ??????????? ?? ???? ??????????? ??????????? ????? ? ?????????????? ??????, ????? ?? ?????? ?????????? ???????, ?? ? ??????? ??????? ?? ???????????, ???????? ??? ???????? ??????? ??????; ?????? ????????? ??? ?????????????? ?????? ??????? ? ????????? ??? ???????, ?????????? ???????? ? ????????, ? ??????, ????????? ????????? ? ???????? ??? ???????? ???????????. ???? ?? ????? ???????????? ????????? ? ?????????, ????? ? 5 ??????? ?? ???????? ??????, ????????? ?? https://individual-design.ru/ – ??? ?????? ?????, ??????? ????? ? ??????? ??????, ??? ?????? ?????? ?????????? ?????????????? ????????.
??????????? ????? ? ??????? financeprofessional.ee .
Signal Tracker – Insightful articles, content guides planning and execution effectively.
??????????? ?????? ?????? ?? ???? ??????????? ?????? ?????? ?? ???? .
progressdrivenforward.click – Great content, helps me keep focused and move forward with my goals every day.
GrowthMap.org – Content communicates steps in a logical order, emphasizing direction and purpose.
forwardmotionguide – Clear and actionable, simplifies progress tracking.
growthmovesclearly.click – Very motivating posts, helps me break down tasks and move forward with confidence.
progresshub – Excellent resource, made it easy to understand key concepts.
progressflow – Organized layout, tracking progress feels natural and easy.
ProgressWithClarity.net – Text is clear, forward motion is easy to grasp.
Signal Compass – Easy-to-follow advice, signals are presented in a way that supports taking action.
????? ?? ??????? ????? ?? ?????? ?????? ????????, ????? ??? ????? ???????? ????????? ? ???. ?????? ????????? ??? ??? ???????? ?????? ?? ?????, ? ?? ?????????? ?????? ??? ?? ??????. ?? ???????? 24 ???? ? ?????, 7 ???? ? ??????, ??? ???????? ? ??????????? ????, ????? ?? ????? ???? ??????? ? ????? ????????? ? ????? ????? ?????. ????????? ??????????????! ?? ??????????? ??????? ???????? ???????????? ? ????????? ????. ???? ????????? – ??? ????????? ??????????? ?????? ? ????? ????????? ????????.
forwardgrowth.click – Helpful strategies, keeps progress moving steadily and logically forward.
?????????? ???????? plazm-sterilizatory.ru .
??????? https://nazenazeblog.com/ ?????????????????????????????????????????????????????????????????????????????????????????????????????????????????????
DirectionFlow – Very clean presentation, makes understanding progress feel natural.
turn plans into action – Encourages execution rather than staying stuck in planning.
SignalPath.net – Layout emphasizes clarity, showing how signals guide direction effectively.
Looking for skid plates for enduro, trials, and motocross motorcycles? Visit https://hardglide.com/ where you’ll find high-quality skid plates, suspension arm guards, engine guards, and other accessories. HardGlide products ship worldwide. Learn more on the website.
fasttrackclarity.click – Clear advice, helps me stay on track and move quickly through my tasks.
muscle growth boy porn
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
motionpath – Super informative, makes motion easier to grasp.
PathToGrowth.com – Layout communicates direction clearly, growth concept feels natural.
???????? Chery ?????? ???????? ???????????? ?????????, ?? ?????????? ????????????????? ???????????? ????????????, ??????? ?????? ? ??????? ??????????? ??????? ? ???????????? ??????????? ??????????. ?? ????????, ??? ?????????? ????? ???????? – ????? ??????????? ? ?????????? ???????????? ??????????. ??????????? ? ????, ?? ????????? ?? ?????? ???????????? ?????????, ?? ? ????????? ????????, ????????????????? ? ????? ??????. ????????? ?????? ??? ?????? ?????????? ??????????!
intentdrive – Very practical platform, everything was easy to locate and use.
Clear, concise, and practical information. I appreciate how easy it is to follow.
momentumnavigator – Excellent guidance, everything is presented clearly and simply.
Action Focus – Practical approach, helps understand how focus drives meaningful steps forward.
????????????? ?????? DreamStalker Expert ?????? ????????? ?????????????? ???????????? ????????????? ???????????? ???????????, ????? ???????? ???????????? ????, ???????? ???????????? ? ???????????? ????????. ?????????? ???????? ?? https://claps.me/catalog/pribory-dlya-osoznannykh-snov/pribor-dlya-osoznannykh-snovideniy-dreamstalker-expert/ ? ??????? ????????? ? ????????? ?????-?????? ? ???????????????? ?????????? tACS. ?????? ?????????? ?????????????? ?????? ??????????, ????????? ????????? ? ??????????? ??????? ???????? ?? ?????????????? ???????.
SteadyPath.com – Presentation feels purposeful, showing consistent direction.
SmallStepsBigImpact – Encouraging tips, keeps momentum steady and natural.
actionablevelocity.click – Amazing content, helps me focus my energy and boost productivity quickly.
ecoenergyhub – Great pointers, I feel driven to apply them right away.
????? ?????? ? ????? ????? ????? ? ??? SEO-???????????, ??????????? ?????? ? ??????? ? ?????? ??????: ???????? ??????? ?????? ? ??????. ?????, ?????????, ???????, ??????????? SEO, ????????? ? ??????? ???????. ???????? ?? ????????? — ???? ?????, ?????? ? ???????.
PowerFlow.io – Simple yet effective, gives a sense of forward motion.
ActionTrail.org – Presentation is engaging, sense of forward movement is highlighted.
growthwithouthassle.click – Nice strategies, makes progress simple and clean every step of the way.
PathwayDrive.net – Layout emphasizes practical steps, showing direction through action.
Excellent resource with valuable information. Thanks for sharing this so clearly.
??????????? ???????? ? ???????, ???????, ?????? ? ??????????? ?? ??????? ?? ????? ?? ?????? ??????, https://kruizy-po-persidskomu-zalivu.ru/
?????? ????? ??????????
focusmoves – Clear and practical platform, everything was easy to find.
signalclarifiesgrowth.click – Actionable content, simplifies growth and provides clear steps to follow every day.
progresscleanly – Shows that methodical progress ensures traction remains effective and efficient.
motioncoach – Well-organized and responsive, content is simple to follow.
Progress Path – Clear guidance, explains how consistent action fosters flow naturally.
focuscoach – Insightful tips, makes it easier to prioritize important work.
FlowWithPurpose – Clear advice that makes approaching long-term projects much simpler.
?Necesitas mudarte? https://trasladoavalencia.es ?Necesitas una mudanza rapida, segura y sin complicaciones en Valencia? Ofrecemos servicios profesionales de transporte y mudanzas para particulares y empresas. ?Solicita un presupuesto gratuito y disfruta de nuestro servicio de calidad!
Allow me to tell you something nearly all septic companies refuse to: there are two categories of people in this reality. Those who assume septic systems are merely “underground boxes for waste,” and those who’ve had raw sewage gurgling into their backyard at the dead of night. I understood this distinction the tough way in 2005—knee-deep in sludge, trembling in a Washington rainstorm, as my siblings and I helped a veteran installer restore our family’s failed system. I was 14. My hands blistered. My clothes were destroyed. But that evening, something crystallized: This is not just manual labor. It’s folks’ lives we’re safeguarding.
Here’s the dirty truth: nearly all septic companies just pump tanks. They are like quick-fix salesmen at a demolition convention. But Septic Solutions? They’re different. It all originated back in the beginning of the 2000s when Art and his family—just kids barely tall enough to lift a shovel—aided install their family’s septic system alongside a weathered pro. Imagine this: three kids knee-deep in Pennsylvania clay, understanding how soil absorption affects drainage while their friends played Xbox. “We never just dig holes,” Art explained to me last winter, hot coffee cup in hand. “We discovered how ground whispers mysteries. A patch of cattails here? That’s Mother Nature screaming ‘high water table.'”
https://x.com/septicsolu
??????????? ???????????? ??????? http://financeprofessional.ee .
??? ??????????? ?????? ?? ??????? ??? ??????????? ?????? ?? ??????? .
https://evakuatorhelp.ru/ ?? ??????? ????? ?? ?????? ?????? ????????, ????? ??? ????? ???????? ????????? ? ???. ?????? ????????? ??? ??? ???????? ?????? ?? ?????, ? ?? ?????????? ?????? ??? ?? ??????. ?? ???????? 24 ???? ? ?????, 7 ???? ? ??????, ??? ???????? ? ??????????? ????, ????? ?? ????? ???? ??????? ? ????? ????????? ? ????? ????? ?????. ????????? ??????????????! ?? ??????????? ??????? ???????? ???????????? ? ????????? ????. ???? ????????? – ??? ????????? ??????????? ?????? ? ????? ????????? ????????.
Allow me to explain something most septic companies will not: there are two types of people in this life. Those who think septic systems are merely “underground boxes for waste,” and those who’ve had raw sewage gurgling into their property at the dead of night. I understood this difference the tough way in 2005—standing in sludge, trembling in a Washington rainstorm, as my brothers and I assisted a veteran installer fix our family’s broken system. I was fourteen. My hands blistered. My jeans were destroyed. But that moment, something changed: This ain’t just digging. It’s people’s lives we’re preserving.
This is the harsh truth: the majority of septic companies just pump tanks. They’re like band-aid salesmen at a disaster convention. But Septic Solutions? They’re different. It all originated back in the beginning of the 2000s when Art and his family—just kids scarcely tall enough to shoulder a shovel—helped install their family’s septic system alongside a experienced pro. Visualize this: three youngsters knee-deep in Pennsylvania clay, understanding how soil absorption affects drainage while their buddies played Xbox. “We never just dig trenches,” Art explained to me last winter, steaming coffee cup in hand. “We understood how earth whispers secrets. A patch of wetland vegetation here? That’s Mother Nature screaming ‘high water table.'”
https://deanopig339.iamarrows.com/why-septic-licensing-standards-matter-more-than-ever-for-puget-sound-protection
SparkPath.org – Layout is clear, highlighting the natural flow from idea to momentum.
FlowDesign.net – Presentation feels clean and communicates growth thoughtfully.
clarity shapes direction – Strong theme that feels consistent and thoughtful.
???????????? ?????????? ?????????????????? plazm-sterilizatory.ru .
focusbuildsresults.click – Content here is clear and concise, perfect for helping me stay on track with my goals.
fasttrackprogress – Very helpful, provides clear methods to advance quickly.
ProgressInsight – Very practical tips that make moving forward simple and doable.
progressfocus – Very user-friendly, platform made understanding and action simple.
leadnavigator – Clear and practical, allows me to access information efficiently.
AttractSignals.net – Idea of traction feels practical, signal approach communicates movement effectively.
ChoiceDrivenGrowth.com – Concept feels empowering, growth presented in a clear, approachable way.
???????? Geely ????? ????????????? ??? ????????? ??????????? ? ????????? ???? ?????????? ????????? ???. ???? ???????????? ????????? ???????, ????? ??? Chery, Lifan, Geely, Great Wall, Haval, Howo, Foton, Faw, Baw, Byd, Changan, Dong Feng, ????????? ?????????? ????? ?? ???????????? ? ?????????????? ????????. ??????????? ????????????? ?????? ? ?????????????? ??????? ???? ??????????? ??????? ????????? ??????????, ?????????? ?????????? ??????? ??????????? ??????? ? ?????????????. ???? ???????? ???????????????? ?? ????????? ????????? ??? ????? ??????? ????????? ????????????? ???????, ????????? ??? ???????????? ?????? ??????????????? ?? ??????????????, ??? ? ???????????? ??????? ?? ??????????? ???????????.
????? ?????? ? ????? https://avigroup.pro/kazan/ SEO-???????????, ??????????? ?????? ? ??????? ? ?????? ??????: ???????? ??????? ?????? ? ??????. ?????, ?????????, ???????, ??????????? SEO, ????????? ? ??????? ???????. ???????? ?? ????????? — ???? ?????, ?????? ? ???????.
steadyclarity.click – Helpful content, emphasizes how consistent steps build understanding gradually.
girls boys porn video
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
growthflowsintentionally.click – Inspiring and practical content, helps me stay focused and move forward effectively.
PowerPath.org – Content feels structured and energetic, conveying movement effectively.
GrowthFocus – Easy-to-follow guidance, makes understanding growth steps simple.
MomentumClarity.org – Presentation feels lively, clarity and action are balanced well.
IdeaVelocity.net – Layout emphasizes forward thinking, showing ideas moving quickly and logically.
?????? ?????????? Individual Design ?????????? ???????????????? ??????? ??????????? ???????????? ????????? ? ????????????? ???????? ? ??????. ????????????? ? ?????? ?????????, ????? ? ???? ??????? ?? ???????? ????????????? ??????, ?????? ???????????????? ?? ?????? ? ??????????????? ? ?????????? ??????????? ??????????? ????????. ?????????? ??????? ????????? ??????????? ??????? ??? ?????????? ?? ????????? ????? ??? ??????????? ?????????? ?????????????? ????????. ????????? ?? ??????? ?????????, ???????????? ? ???????? ??????? ????? ?????? ?? https://individual-design.ru/ ??? ???????????? ??????? ??????????? ?????. ???????????????? ??????? ??????? ????????? ????? ???????????? ???? ??? ?????? ??????????.
actionhub – Organized pages, finding exactly what I need is simple.
????? ?????? ?????????? ?????????? ??????? ? ???????????? ? ?????????? ??????????? ??????? ? ?????????? ?????????? ??? ????? ????? — ???????, ?????, ????????, ?????? ??????. ??????? ?????, ????????? ??????, ?????? ?????? ? ??????????????? ?? ??????????? ?????? ?????????.
PWA ??????
?????????? ???????????? ?????????? ???????????? .
clarityguidesvelocity.click – The clarity in these posts helps me focus on what needs to be done and take action faster.
forwardmotionguide – Helpful insights, I now know the best steps to take.
SignalDrivenFlow.io – Presentation emphasizes clarity and structured growth, anchored in signal concepts.
?????? ?? ??????? ???????? ???????? ??? ?????? ???? ?????. ??????????? ??????, ???????? ? ???????????. ?????????? ????????? ??????????? ??????????. ?????? ?????????? ?? ??????? ?????????. ??? ????????? ??????? ?????? ???????. ? ????? ?????? ???????? ?????? ??????? ????????? ??????? – http://www.forum.alyno.ru/phpBB2/profile.php?mode=viewprofile&u=61432. ???? ?? ?????? ???????? ????????? ?? ???? ????, ????? ??????? ??????? ????????. ???????? ?????????? ?? ?????????. ??? ???????? ??????. ??????? ?????? ?? ?????? ??????? ???????
kraken ???????
EnergyAndFocus – Useful guidance, maintains focus and movement in projects naturally.
id ????? ??????? https://financeprofessional.ee/ .
?? ????? ??????? ?????? ?????
growththroughclarity.click – Useful guidance, direction simplifies actions and improves outcomes.
StructuredGrowth.net – Approach feels organized, growth ideas are communicated effectively.
progressguide – Straightforward and helpful, found exactly what I needed quickly.
ProgressFromThought.net – Layout conveys optimism and direction, showing ideas as catalysts for action.
signalpowersdirection – This platform really clarifies how signals can guide actions effectively.
????? ? ???? ??????? ????????? ???? ????????? ????????? ? ????????? ? ??????? ?????? ??????? ? ????????. ???????? ? ??????? ? ????????????????. ?????????? ??????????????, ? ?? ??????? ? ?????? ???? ??????????? ????? ?????????????? ????? ? ???? ?????????? ??????. ??????? ???? ???? ? ????? ????? ? ??????? ??? ???????!
?????????? ????????????? ?????????? ????????????? .
Let me explain something most septic companies won’t: there are two categories of people in this life. Those who assume septic systems are simply “buried containers for waste,” and those who have had raw sewage erupting into their yard at midnight. I discovered this reality the difficult way in 2005—knee-deep in muck, shivering in a Washington rainstorm, as my family and I helped a weathered installer fix our family’s broken system. I was 14. My hands ached. My pants were destroyed. But that moment, something clicked: This isn’t just dirt work. It’s folks’ lives that we’re preserving.
Let me share the dirty truth: nearly all septic companies just service tanks. They act like band-aid salesmen at a chainsaw convention. But Septic Solutions? These guys are different. It all originated back in the early 2000s when Art and his siblings—just kids scarcely tall enough to shoulder a shovel—assisted install their family’s septic system alongside a grizzled pro. Picture this: three youngsters knee-deep in Pennsylvania clay, learning how soil permeability affects drainage while their peers played Xbox. “We never just dig trenches,” Art explained to me last winter, steaming coffee cup in hand. “We discovered how ground whispers truths. A patch of wetland vegetation here? That’s Mother Nature yelling ‘high water table.'”
https://zixo8.mssg.me/
????????????????? ??????? “?????? ????” ? ???????? ???????????????? ?? ??????? ? ???????? ???????????? ? ???????????? ??????? ??? ????????. https://kinder-dent-lyubertsy.ru/ ?????????? ?????? ?????? ?????: ?? ???????????????? ??????? ? ??????? ??????? ?? ???????????, ?????????????? ? ??????????. ????? ??????????? ???????? ????????, ? ??? ????? ???????? Vector ??? ??????????????????? ????????. ????????? ????????????? ??????????????????????? ???????????, ????????????? ? ?????????????? ??????????. ???????? ????????? ??????????? ?????, ????????? ???????, ??????? ? ????????? ??????????????, ???????????? ? ???????? All-on-4/6.
FocusedAction – Inspiring content, encourages me to keep building momentum daily.
signalcreatesmomentum – Great content, inspires me to build momentum consistently in tasks.
?????? ?? ????? ???????? ???, ??? ????? ????????? ??????? ? ??????? ??????? ???????? – https://kruizy-iz-kataya.ru/
????? ???? ??????? ????????? ?????? ?????? ???????? ?? ???? ??????? ? ???????????? ???????????? ?? ???? ???????? ????? ? ?????? ? ???????. ?? ??????? ??? ??????????? ? ??????? ?????????? ????????????????, ??????? ??????????????? ? ???????????. ?? ?????????? ?????????????? ???????, ??????????? ???? ?????? ?????????????? ? ???????????.
intentengine – Efficient and well-structured, platform made everything simple.
forwardtracker – Smooth navigation, reviewing progress is fast and simple.
?????? darknet tor
Allow me to tell you something the majority of septic companies will not: there are two categories of people in this life. Those who assume septic systems are simply “subterranean tanks for waste,” and those that have had raw sewage gurgling into their yard at the dead of night. I learned this difference the difficult way in 2005—waist-deep in sludge, shivering in a Washington rainstorm, as my siblings and I assisted a veteran installer repair our family’s collapsed system. I was fourteen. My hands blistered. My clothes were wrecked. But that moment, something crystallized: This isn’t just digging. It’s families’ lives we are safeguarding.
Here’s the harsh truth: the majority of septic companies just maintain tanks. They are like quick-fix salesmen at a chainsaw convention. But Septic Solutions? They’re unique. It all started back in the beginning of the 2000s when Art and his family—just kids barely tall enough to carry a shovel—assisted install their family’s septic system alongside a weathered pro. Imagine this: three kids knee-deep in Pennsylvania clay, discovering how soil permeability affects drainage while their friends played Xbox. “We didn’t just dig ditches,” Art shared with me last winter, hot coffee cup in hand. “We discovered how earth whispers mysteries. A patch of marsh plants here? That’s Mother Nature shouting ‘high water table.'”
https://www.brownbook.net/business/54543470/septic-solutions-llc
PathToSuccess.io – Easy to follow, direction helps clarify the growth message.
????? ???? ???????? ????????? ??? ?????????? ? ?????, ??????? ???????, ??????? ?? ????? ? ??????? ??????????? https://kruizy-iz-kataya.ru/
progress with purpose – The message stays clear and feels thoughtfully structured.
Game-Lands https://game-lands.ru/ – ??? ???? ? ?????????? ??????? ? ????????????? ??? ???????? ? ??????? ???????. ????? ?? ??????? ?????? ??????, ??????? ????? ? ??????, ?????? ???????????? ?????????, ????????, ????????, ? ??????????? ????? ?? ???????. ???????, ??? ???????? ?????? ??????????, ??? ?????? ? ??????? ???????? ? ? ???? ?????? ? ????? ?????. ???, ????? ???????? ????? ? ???????? ??? ??????????? ??????? ???????.
????? ??????? ?????? ????? ?????? ????? ??? ?????????
?????? ??????? ??????
ClarityPath – Very actionable, allows me to track progress and stay on course easily.
?????? login
?????????? ???????????? ???????????? plazm-sterilizatory.ru .
progressinsights – Clear guidance, made understanding tasks much faster.
SignalMomentum.net – Layout highlights natural flow and clear messaging throughout.
? ?????? ???????????, ? ?????, ?????????? ??????? ???????? “??? ????”, ???????????? ???????? ??????????? ???????? ???????? ???????? ? ???????????? ????????, ???????? ?????????????? ? ???????? ???????. ?????????? ????????? ????? ??????, ?????, ?????, ?????, ??????? ???????????? ????????????? ???????? ? ?????????? ????????????, ??? ????????????? ? ??????????? ???????? ??????. ?? ???????? ????????? ? ??????????: ??????, ?????????, ????????, ?????????, ???? ???????????? ?????????, ????, ??????? ? ?????, ????? ????? 500 ???????????? ?? ??????????? ?????????? ???????????. ????????????????? ???????? ?????????? ??????, ???????? ? ???????, ?????????? ???????????? ???????? ?? ???????? ?????. ???????? https://sadovodklin.ru/ ????? ???????????? ? ?????????, ??????? ? ???????, ??? ??????? ???????? ?? ????? ?? ????? ? ??????? ???????? ?????? ??????, ? ???????? ????? ????? ?????? ??? ?? ???????? ??? ??????????.
progressflow – Smooth interface, locating key resources is straightforward.
???????? ?????????? ???????????? ????? ?????????? ????????? ?????????? ??????????, ???????? ????????????? ???????? ? ????????? ???????, ????????????? ???????? ???????????????? ????????. ?? ???????? ???? ????????? ?? ?????????????? ??????? ?????? ??????, ?? ?????? ???? ??-????? ?? ?????????? ???? ???? ??????? — ?????? ?????? ??????????? ?????? ???? ?????. ???? https://crimea-trip.ru/ ?????? ???????? ?????????? ? ????????, ??????, ????????????? ????????? ? ???????????????? ???????????? ???????, ??????? ???????????? ???????????? ??????????? ? ?????? ???????. ????? ?? ??????? ?????? ?? ?????? ?????, ???????? ????????????? ???????? ? ???????????? ?? ??????????????? ??????????, ????????? ????????? ?????????? ????????? ???????? ????????? ????????? ? ???????????? ??????? ?????? ???????.
advanceinsight – Clear, structured content with smooth navigation makes the site user-friendly.
keep advancing – Communicates steady progress and continued movement.
FocusedEnergyBoost – Inspiring suggestions, makes workflow feel manageable and energetic.
?????? ????
?????? onion
direction fuels progress – Ends with a strong sense of clarity and purposeful motion.
kraken ????
?????? ???????
anchortrack – Well-organized platform, finding directions is effortless.
forwardthinkinglogic – Highlights how applying logical planning moves projects forward efficiently.
guided forward flow – Creates a sense of smooth, intentional progress.
focus keeps things steady – The structure supports clarity without distraction.
Excellent resource with valuable information. Thanks for sharing this so clearly.
I need to tell you something nearly all septic companies will not: there are two kinds of people in this reality. Those who think septic systems are simply “subterranean tanks for waste,” and those that have had raw sewage gurgling into their property at the dead of night. I understood this difference the tough way in 2005—knee-deep in mud, trembling in a Washington downpour, as my brothers and I helped a grizzled installer restore our family’s broken system. I was fourteen. My hands blistered. My jeans were destroyed. But that night, something changed: This ain’t just manual labor. It’s people’s lives that we’re protecting.
Let me share the harsh truth: nearly all septic companies just service tanks. They are like quick-fix salesmen at a disaster convention. But Septic Solutions? These guys are special. It all started back in the early 2000s when Art and his brothers—just kids scarcely tall enough to lift a shovel—assisted install their family’s septic system alongside a grizzled pro. Visualize this: three kids buried in Pennsylvania clay, learning how soil absorption affects drainage while their peers played Xbox. “We never just dig holes,” Art shared with me last winter, warm coffee cup in hand. “We understood how soil whispers truths. A patch of marsh plants here? That’s Mother Nature screaming ‘high water table.'”
https://about.me/septicsolutionsllc
moveforward – Simple to navigate, found all the information I needed.
claritymap – Very user-friendly, I located information immediately.
Allow me to tell you something nearly all septic companies won’t: there are two kinds of people in this life. Those who believe septic systems are merely “underground boxes for waste,” and those who’ve had raw sewage gurgling into their yard at 2 AM. I understood this difference the difficult way in 2005—knee-deep in sludge, trembling in a Washington rainstorm, as my brothers and I assisted a veteran installer restore our family’s failed system. I was fourteen. My hands were raw. My clothes were wrecked. But that night, something crystallized: This isn’t just manual labor. It’s folks’ lives we are protecting.
This is the ugly truth: the majority of septic companies just service tanks. They’re like quick-fix salesmen at a demolition convention. But Septic Solutions? They’re different. It all started back in the early 2000s when Art and his siblings—just kids barely tall enough to lift a shovel—assisted install their family’s septic system alongside a weathered pro. Visualize this: three kids buried in Pennsylvania clay, learning how soil absorption affects drainage while their buddies played Xbox. “We never just dig ditches,” Art shared with me last winter, hot coffee cup in hand. “We discovered how earth whispers truths. A patch of cattails here? That’s Mother Nature shouting ‘high water table.'”
https://codymqyp338.timeforchangecounselling.com/how-local-soil-conditions-impact-septic-performance-across-washington-counties
?????? login
Gibddinfo.ru — ??? SEO-????? ??? ???????????? ? ?????????? ?????????????, ??? ????? ???????? ????????? ???????????, ?????????? ?????? ?????? ? ?????????? ????????? ? ????? ?????? ?? ???????????? ???????. ????????? ??????? ??? ???????? ???, ????????? ? ?????? ???????, ??? ?????? ?? ??????? ????????? ??? ????????????????? ?????. ?????????????? ? ?????????? ? ?????? ?????????? ????? ?? https://gibddinfo.ru/ — ????? ?????????? ??, ??? ????? ???????? ??????, ?????????? ?????? ? ????? ???????? ?????? ??????????? ? ??????? ????????? ??????????? ? ????????-??????????.
?????????? ?????????? ???????? ???????????? ??????? ??????? ??? ????????? ? ????????. ????????, ??????????????? ? ????????? ? ????? ???????. ???????? ????????? ? ??????????, ????????? ?????? ??? ????? ?????. ????????? ??????, ??? ????????.
take action find paths – Communicates opportunity without feeling overwhelming.
???????? «????????» ???????? ?? ????? ?????????????? ? 2005 ???? ? ?????????? ?????? ???????? ????? ????? ????????? ?? ????? ?????????????. ? ???????? https://www.trub-prom.com/ ??????????? ??????? ??????????? ?????????: ?????????, ??????????????, ???????????, ????????? ????? ????????? ????? ????? ? ????????????. ??????????? ????? ??????-????????? ???????? ?? ?????? ? ??????? ? ???????????????? ? ????? ?????? ??, ??????????? ???????????? ?????????? ? ??????? ???????? ?????????.
?????????????????? ????????????? plazm-sterilizatory.ru .
?????? ??????
DreamStalker Expert — ?????? ?????????? ????????? ??? ???, ??? ?????????? ?????????? ?????????? ? ????? ????????? ??????????? ???? ? ??????? ???????? ? ???????? ???????? ? ???? REM. ????? ???????? ????????????? tACS ? ??????? ???????????, ???????? ?????????? ?????? ??? ?????????????? ??????????? ???. ???????????, ???????????? ? ????? ???????? ?? https://claps.me/catalog/pribory-dlya-osoznannykh-snov/pribor-dlya-osoznannykh-snovideniy-dreamstalker-expert/ — ? ?????????? ????????? ? ??????? ?????????.
focused path forward – Message is simple and lands without confusion.
kraken mirror
BTB Connect — ???????????? ??????? ?????? ? ???????? ??????? https://btbconnect.ru/ – ???????? ????????? ??? ?????????? ? ??????????????? ?????-???????. ?????? ???????????? ?? ????????, ??????? ???? ????? ??????? ???????? ??????????????, ????????? ? ???????? ???????????. BTB Connect ?????????? ?????? ? ?????????????? ????????, ???????? ?????? ??? ??????????? ????? ? ??????????????.
?????? ?????????? ??????
????? ??????????? ???????? ??? ?????????? ?????????? ? ??????, ??? ? ???? ?????? https://doskadonbassa.ru/ ?????????? ?????????? ?????????? ? ?????????? ????-????, ????????????, ?????? ? ??????. ??????? ????????? ????????? ?????? ????? ?????? ?????? ??? ?????????? ???? ?????? ??????? ?????????????. ?????? ???????? ??? ???????????, ??????????? ?????? ??????? ????? ?????????? ? ????????????. ??????????? ???????? ????????? ?????, ? ?????????? ?????????? ????????? ?????????!
Play Lightning Roulette Online on the official website https://lightningrouletteplay.com/en/ . Learn how to play Lightning online roulette, as well as how to register an account, make a deposit or withdrawal, and learn game strategies. And be sure to take advantage of our lucrative bonuses and promotions!
kraken ??????? ??????
?????? mirror
take action find paths – Communicates opportunity without feeling overwhelming.
?????? ?? ????? ?? 14 ?????? ?????? ?????
????? ????????? ?????????? ??????? ???? : ????????, ???????? ?????? ? ???????, ???????? ? ?????????. ???????? ????????? ??? ????? ?????, ????????? ?????????? ?????? ? ?????????? ??????. ?????????? ?????? ? ??????? ?????.
kraken ???????
SmartWeeklyFocus – Encouraging tips, helps me break down tasks into achievable steps.
?????? ?????
?????? ??????
?????? darknet tor
????? ?????? ???? ?????? ? ?????? ???????? ???? https://bs-service.com.ua/ – ??? ?? ??????? ?????? ???????????????? ?????? ?? ??????? ?????????????, ? ????? ?? ???????????? ???????????. ??????? ???? ??????????????? ???? ?? ?????, ????? ???????? ?????? ?? ???????????? BS Service.
energy follows direction – Simple idea presented clearly, momentum feels easy to grasp.
kraken
I need to share with you something nearly all septic companies won’t: there are two types of people in this reality. Those who assume septic systems are merely “underground boxes for waste,” and those that have had raw sewage gurgling into their property at the dead of night. I discovered this difference the difficult way in 2005—knee-deep in mud, trembling in a Washington deluge, as my brothers and I aided a veteran installer restore our family’s collapsed system. I was fourteen. My hands blistered. My jeans were wrecked. But that night, something clicked: This ain’t just digging. It’s people’s lives we are protecting.
Here’s the dirty truth: the majority of septic companies just pump tanks. They are like temporary salesmen at a disaster convention. But Septic Solutions? These guys are different. It all originated back in the beginning of the 2000s when Art and his brothers—just kids barely tall enough to carry a shovel—aided install their family’s septic system alongside a weathered pro. Picture this: three kids waist-deep in Pennsylvania clay, learning how soil porosity affects drainage while their peers played Xbox. “We didn’t just dig trenches,” Art explained to me last winter, steaming coffee cup in hand. “We learned how earth whispers truths. A patch of wetland vegetation here? That’s Mother Nature yelling ‘high water table.'”
https://rentry.co/uvbw467a
????? ?????? ????? ??? ??????? ???????? ?????? ?????
StepByStepDirection – Easy-to-digest content, helps me grasp ideas quickly.
?????????? ????????????? ????????????? plazm-sterilizatory.ru .
build forward momentum – Practical tone that supports consistent action.
kraken ????
kraken ?????
IncrementalProgress – Inspiring approach, makes slow but steady gains feel achievable.
do something gain energy – Reads naturally and highlights how action creates forward drive.
???????? ???????? ?????????? ??????????? ??????? ??? ???????? ????????????? ???????? ?? ?????????? ????????. ? ???????????? https://profprud.ru/ ???????????? ????? 250 ????????????: ?????? ??? ? ??????????????? ??????, ??????? ??????????? ????? ???????????? ????????????, ???????????????? ???????, ??????, ????????, ????????? ???????????? ? ???????????? ????????. ?????????????? ? ??????????????? ?? ????????, ??? ? ?????? ????? ??????????? ??????????? ???????? ????????? ? ????????? ?? 10 ???.
?????? ???? ?? ???? ????? ????? ????? ????????
?? ????? ?????????????? ?????????? ????????? ????? Glassway ???????? ? ???????????? ???????-?????? ????????? ????????, ??????????? ??????????? ? LED-????????????, ???????????? ???????? ??? ???????, ???????????? ? ???????????????? ???????????. ? ????? ??? 10-?????? ??????, ????? ???????????? ?????? ???? ?? ?????????????? ?? ???????, ????????? ????????????? ?????????? ? ?????????, ??????????????? ?????????? ????????????. ????? ?????????? ????????? – ???????????? ? ??????? ???????, ?????????? ??????????? ? ?????-???????, ? ????? ????????????????? ???????????, ??????? ??? ???????? ????? ???????, ??? ???? ? ???????? ??????? Seasons. ????? ?????? ?????????? ?????????? ???????????? ???????? glassway.group, ????? ???????????? ? ????????? ? ???????? ??????????????????? ??????? ? ????????? ???????? ? ??????????? ????????? ?? ???? ??????. ??????? ???????? ?????????? ? ???????? ??????????, ??????????? ????????? Glassway ??? ???-?????????? ? ???????????? ???????.
quickimpactideas – Shows that quickly acting on ideas creates immediate impact and measurable progress.
??????????? ???????? ??????? ?? ?????? ??????????, ?? ? ?????????? ???????, ???????? ????? ???? ???? ? ?????????? ? ?????????? ?????????? ??? ?????????????? ?????? ????????????. ??????? ??????? ?? ???????? ? ????? ????????? ???????????? ????????? ?????????????, ???????????? ? ???????? ? ???????????? ???????????? ????????? — ?? ???????????? ?? ??????????? ?????? ? ????????? ???????? ??????. ????????????? ???????? ?????????? ??????? ????????? ?????????? ?????? ??????? ???? ? Cesal, ?????????? ??? ??????????? ???????? ??? ??????????????? ????????? ??? ??????????? ????????????. ?? ????? https://potolki-52.ru/ ???????? ??????? ??????????? ??? ??????? ????????? ??? ?????????? ??????? ?????????, ? ????? ????????? ???????? ????????????? ? ????????? ???????. ??????????? ??????????? ?????? ?? ???? ?? ?????? ??????????? ????????? ???????????? ??????????? ??? ????? ??????????? ??????? ???????? ??? ???????????.
?????? ???????
???????? ?????? ?? ?????????? 23 ??? ?????????? ????????? ???????????? ??????????? ??????? ? ???????? ???????, ??????????? ??????????? ?????? ?? ?????????? ??????? ?? ??????????? ????? ?? ?????. ????? ?????? ??????????????? ??????? ??????????? ????? ???????? sakura.spb.ru ???????????????? ?? ?????????? ?????????????? ????????, ??????? ???????? ????? ????? ?????????, ??????? ???????? ????, ????? ??????, ??????? ? ?????????? ????????, ???? ???????. ? ????????? ???????? ?????????????? ????? ?????? ?????????????? ????????, ??????????? ???????????????? ? ??????????? ??????????????? ??????????.
InsightClarity – Motivates improvement with practical, actionable advice.
?Necesitas mudarte? https://trasladoavalencia.es ?Necesitas una mudanza rapida, segura y sin complicaciones en Valencia? Ofrecemos servicios profesionales de transporte y mudanzas para particulares y empresas. ?Solicita un presupuesto gratuito y disfruta de nuestro servicio de calidad!
?????? darknet
?????????? ?????????? ???????????? ?? ??????? ??????? ??????? ??? ????????? ? ????????. ????????, ??????????????? ? ????????? ? ????? ???????. ???????? ????????? ? ??????????, ????????? ?????? ??? ????? ?????. ????????? ??????, ??? ????????.
kraken login
I need to share with you something most septic companies won’t: there are two categories of people in this reality. Those who believe septic systems are simply “underground boxes for waste,” and those who have had raw sewage erupting into their property at the dead of night. I discovered this difference the tough way in 2005—knee-deep in muck, freezing in a Washington rainstorm, as my brothers and I aided a weathered installer restore our family’s broken system. I was fourteen. My hands blistered. My jeans were ruined. But that evening, something crystallized: This ain’t just dirt work. It’s folks’ lives we are safeguarding.
Let me share the harsh truth: nearly all septic companies just maintain tanks. They’re like quick-fix salesmen at a disaster convention. But Septic Solutions? They are special. It all started back in the beginning of the 2000s when Art and his siblings—just kids hardly tall enough to shoulder a shovel—helped install their family’s septic system alongside a weathered pro. Picture this: three kids buried in Pennsylvania clay, learning how soil absorption affects drainage while their friends played Xbox. “We never just dig ditches,” Art told me last winter, hot coffee cup in hand. “We understood how ground whispers mysteries. A patch of marsh plants here? That’s Mother Nature screaming ‘high water table.'”
https://myanimelist.net/profile/blandahtfz
??????? ????-?????????? tgram.link ? ????? Telegram 2026: ???????, TON-????, AI-??????? ? ??????-???????????. ??????, ????????, ?????????? ? ??????????. ?????? ?? ??????????, ???????????? ? ???????? ?????? — ??? ? ????? ?????.
FocusedExecution – Very practical suggestions, helps complete tasks with clarity.
????? ?????????? ???????? ????????? ?????? ??? ????????, ???????? ? ???????. ?????????? ?????? ? ??????? ? ????????, ?????? ?? ????, ???????? ? ??????. ?????? ??????, ??????? ????? ? ???????? ?????????.
????????? ??? 1? 1s-erp-vnedrenie.ru .
????????? ???????????? ????????? ???????????? .
????????? ???????????? vodoponijenie-iglofiltrami-msk.ru .
kraken ?????????? ??????
???????????? ?????????? plazmennye-sterilizatory.ru .
????????????? 1? ?????? ????????????? 1? ?????? .
?????????? ??????????? ????????????? ?????????? ??????????? ????????????? .
ClarityForGrowth – Easy-to-follow suggestions, keeps my focus sharp and goals clear.
?????? ??????????? ????
????????? ??????? ????? ??????????? ?? ??????????? ? ????????? ????????? ????????? ????? ?? ????? ????. ????????????? ?????????? ??????? ????????? ??????? ??????????? ?????????, ????????? ?????????????????? ??????? ? ??????? ???????????? ? ?????????? ???????????. ?????? GameBox ?????????? ????????????? ???????? ??????? ?????????? ??? ?????? ???????? – ?? ????????? ??????? ?? ??????????? ??????? ???? Black Shark ? Asus ROG. ???????? ???????????????? ?????????????????? ? ?????????? ????? ????? PUBG Mobile ? Genshin Impact. ???????????? ? ????????? ??????? ????? ?? ?????? https://gamebox.biz/podborka-igrovyh-smartfonov/1000028296/ ??? ???????????? ??????????? ?????????????? ? ???????????? ?? ?????? ???????????? ?????????? ??? ?????????? ????????.
kraken ??????? ???????
Let me explain something nearly all septic companies won’t: there are two categories of people in this life. Those who believe septic systems are simply “underground boxes for waste,” and those who have had raw sewage bubbling into their property at the dead of night. I understood this distinction the difficult way in 2005—knee-deep in mud, shivering in a Washington rainstorm, as my family and I assisted a weathered installer fix our family’s collapsed system. I was fourteen. My hands ached. My clothes were destroyed. But that evening, something changed: This isn’t just digging. It’s families’ lives we’re safeguarding.
Let me share the dirty truth: the majority of septic companies just service tanks. They are like quick-fix salesmen at a chainsaw convention. But Septic Solutions? They are special. It all originated back in the beginning of the 2000s when Art and his brothers—just kids scarcely tall enough to shoulder a shovel—helped install their family’s septic system alongside a weathered pro. Visualize this: three kids buried in Pennsylvania clay, understanding how soil permeability affects drainage while their friends played Xbox. “We did not just dig holes,” Art shared with me last winter, steaming coffee cup in hand. “We learned how soil whispers secrets. A patch of cattails here? That’s Mother Nature yelling ‘high water table.'”
https://go.bubbl.us/ef4627/1ba6?/Bookmarks
https://mixtum.online/ is a premium Bitcoin mixer that will provide you with an unrivaled level of anonymity. Learn more about all our advantages on our website and try out our new mixing mode with unique processing parameters. We offer a free trial and no registration required.
????? ??????? ????? ?????? ?? ????? ?????
SignalPathways – Very clear tips, allows me to plan and act with confidence.
?????????????????? ??????? https://tvoyprud.ru/ ?????????? ??????????? ??????? ??? ???????????? ????????????? ????????: ??????????????? ? ??? ??????, ??????? ??????????? ?????, ?????? ??? ???????? ? ????????? ??????? ??????? OASE, Jebao, Messner, ??????? ?????????? ? ???????. ???????????????? ????????????, ??????? ??????????? ???????????? ? ??????????? ??? ??????? ??????? ??????? ????????? ???????????? ???? ????? ?????????.
??????? ????????????? ????????????? iglofiltry-vodoponizhenie.ru .
????????? erp ????????? 1? ????????? erp ????????? 1? .
kraken ???????
????????????? ????????????? ????????????? ????????????? .
PWA ??????
kraken mirror
EnergyAndFocus – Helpful content that motivates action and consistent effort.
kraken ?????
?????? ????? ?? ????? ??????? sugar marina resort cliffhanger aonang 4 ?????
immediateideaaction – Demonstrates that taking immediate action on ideas drives strong and measurable outcomes.
????????????? ??????? 1? ?? ??????????? 1s-soprovozhdenie.ru .
?????????? ????????????? ?????????? ????????????? .
???????????? ?????????? plazmennyy-sterilizator.ru .
kraken mirror
????????? erp ?????? ????????? erp ?????? .
??????? ????????????? ????????????? iglofiltry-vodoponizhenie.ru .
????? ??????? ??? ????????? ?? ?????? ?? ????? ?????
?????? darknet market
??????? ??????? ??????? ??????? ? ??????? ???????? – ?????????? ???????? ?? ??????? ???????, ??????????? ????????? ???????, ????????????? ?????? ? ???? ?????, ???????? ????? ???????????, ???????????? ???????? ? ?????? ???????. ??????? ??????? ???????? ??????? ? ????????????? ??????? ???????????? ????, ??? ?????? ???? ?????????? ?????? ???????, ???????? ?? ????? ????????? ?????.
????? ??????? ????? ?????????????? ????????? “Individual Design” ? ?????? ????? ????????? ??? ????? ?? ????????? ?????? ?? ????, ??????? ???????????? ? ???????? ??????? ???????? ?? ???? ??????? ??????? LLumar, SunTek ? 3M. ????? ??????? ? ??????????? ?????? ?????????? ??????? ????? ? ???????????? ????????? ?? ????????? ????, ??????????? ?? ?????? ???????????? ????????????, ?? ? ???????? ?????? ?? ?????? ? ???????, ??? ???????? ????????? ? ??????? ?????????? ????????; ????????? ??? ?????????????? ?????? ????? ????????? ? ????????? ??? ??????, ?????? ?? ???????????? ???????????? ????????, ? ???? ??????? ???????? ????????? ? ???????? ??? ?????????? ????????. ???? ?? ????? ???????????? ????????? ? ?????????, ????? ? 5 ??????? ?? ???????? ??????, ????????? ?? https://individual-design.ru/ – ??? ?????? ?????, ??????? ????? ? ??????? ??????, ??? ?????? ?????? ?????????? ?????????????? ????????.
?????? tor ???????
kraken ??? ???????
Let me explain something the majority of septic companies won’t: there are two types of people in this reality. Those who believe septic systems are simply “buried containers for waste,” and those who have had raw sewage erupting into their property at midnight. I discovered this distinction the hard way in 2005—waist-deep in mud, freezing in a Washington rainstorm, as my family and I helped a weathered installer repair our family’s failed system. I was a teenager. My hands ached. My jeans were destroyed. But that moment, something changed: This isn’t just digging. It’s people’s lives we are safeguarding.
Let me share the harsh truth: the majority of septic companies just pump tanks. They are like temporary salesmen at a demolition convention. But Septic Solutions? They’re unique. It all began back in the early 2000s when Art and his siblings—just kids scarcely tall enough to shoulder a shovel—aided install their family’s septic system alongside a experienced pro. Visualize this: three kids buried in Pennsylvania clay, understanding how soil porosity affects drainage while their buddies played Xbox. “We didn’t just dig holes,” Art told me last winter, hot coffee cup in hand. “We discovered how soil whispers mysteries. A patch of cattails here? That’s Mother Nature shouting ‘high water table.'”
https://zenwriting.net/abbotsnnxe/the-future-of-septic-services-higher-standards-fewer-failures-cleaner-water
????????? ???????????? vodoponijenie-iglofiltrami-msk.ru .
???????????? ???????? ????? ???????? ????? ?????????? ??????????? ?????????, ?????????? ???????????? ??????? ? ??????????. ??? ???????????? ???????? ??????? ?????? ???????, ?? ????????? ?? ???????. ?? ???????? ???????? ??????? ? ?????????????? ????????????.
?????? ?????????? ??????
?????? ??? ???????
1 ? ????????????? ? ????????? 1s-soprovozhdenie.ru .
xrumer ???????? ???????? xrumer 23
?????????? ????????????? ?????????? ????????????? .
?????????????? ????????????? ?????????????? ????????????? .
????????? erp ?? ??????????? ????????? erp ?? ??????????? .
kraken tor ???????
kraken ??????? ???????
kraken ????
??????- ? ?????????????? ?????
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
?????? ??????????? ????
kraken darknet market
?????????? ??????????? ????????????? ?????????? ??????????? ????????????? .
xrumer ??????? xrumer ??????????? ???? ????????
?????? ?? ????? ???????? ??????, ??????????? ? ????? ?????? ?????????????: https://kruizy-iz-kataya.ru/
?? ????? ?? ?????
kraken ??????????? ????
??????-????????? https://rosseriaall.net/ ?????????? ?????????? ???????? ?????????? ???????? ? ??????? ???????? ??? ???????????. ??????? ???????? ?????????, ?????????, ???????????? ???????, ??????? ?????, ???????, ????????, ?????????? ? ???????? ??????? ? ??????? ??????????? ?? ?????? ? ?????. ???????? ??? ???????????? ??????? ??????? ???, ??? ? ??????? 2025 ????. ?????????? ?????????? ???????? ? ??????????? ????????? ????????? ?????? ????? ???????????? ?????? ? ?????? ???????? ? ????? ?????.
I need to explain something most septic companies refuse to: there are two categories of people in this life. Those who assume septic systems are merely “underground boxes for waste,” and those who’ve had raw sewage bubbling into their yard at midnight. I understood this distinction the difficult way in 2005—standing in mud, shivering in a Washington rainstorm, as my brothers and I assisted a weathered installer repair our family’s failed system. I was fourteen. My hands ached. My jeans were wrecked. But that evening, something changed: This isn’t just manual labor. It’s families’ lives we are preserving.
Here’s the dirty truth: most septic companies just pump tanks. They act like quick-fix salesmen at a chainsaw convention. But Septic Solutions? They are different. It all began back in the beginning of the 2000s when Art and his siblings—just kids scarcely tall enough to lift a shovel—assisted install their family’s septic system alongside a grizzled pro. Imagine this: three kids knee-deep in Pennsylvania clay, discovering how soil permeability affects drainage while their buddies played Xbox. “We never just dig trenches,” Art told me last winter, warm coffee cup in hand. “We discovered how earth whispers mysteries. A patch of cattails here? That’s Mother Nature screaming ‘high water table.'”
https://griffinyqnr991.overblog.fr/2025/12/the-role-of-septic-oversight-in-preserving-drinking-water-quality.html
????? ??????? ??????????? ??????? ????? ????? ??? ?????????? ?????????, ??????? ??????? ?????? ??????????? ?????? https://kruizy-po-persidskomu-zalivu.ru/
????????????? ????????????? ?????? vodoponijenie-iglofiltrami-msk.ru .
ChannelMomentum.io – Complex topics are presented clearly, helping readers understand immediately.
????????????? 1? ?????? ????????????? 1? ?????? .
?? ????? ?? ?????
?????????????????? ?????????? ???????????? ?????????????????? ?????????? ???????????? .
ActionMomentum.org – Supports structured execution while keeping motivation high.
xrumer ?????? ???????? Xrumer 19 ????????
????? ?? ????? ????????? ??????? ??????? ???????, ??????? ????????????, ???????? ???????????????? – ????? ?? ????? 2026
????? ?? ????? ?????????? ??????? ??????? ???????, ?????????? ????????? ? ????? ????????? ???????? – https://kruizy-iz-kataya.ru/
????? ?????????? ?????? ?????? ?? ?????, ?????? ???? ????? ???????????, ??? ???? ?? ????? ????????? ?????????? ? ?????? ????? – https://kruizy-iz-kataya.ru/
?????? ????? ??????????
???????? ???? https://priority-auto.ru/ – ?? ????????? ??????????? ?????????, ?????????, ???????? ?????????? ? ????????? ? ???????????? ???????, ? ???????? ?? ????????? ? ??????? ????????? ? ??. ??????? ??? ???? ????? ????????????? ?? ????? ??? ?????????????? ?????? “?????????? ?????????” – ??? ?? ??????? ???????? ????????? ????. ???????? ???? ??? ??? ??????, ?????? ?????????? ????????? ? ?????????, ??? ????? ??????????.
??????????? ?? ??????? ?? ????? ????? ????? ?? ????? ????? ???????????, ?????? ?? ????? ?? ??????? ??????, ??????? ????????, ???????? ???????????, ? ??? ????? ??????????? ?????? ????????? ?????????? ? ?????? ????? https://kruizy-po-persidskomu-zalivu.ru/
ChoiceFlow.net – Steps guide users toward clear decisions with minimal stress.
??? ????? ?? kraken ???????
?????????? ????? ?? ???????????? ????????? ? ?????? ???????? ????????????? ?? ?????? ? ????????????? ???????? CarTrip ?????????? ??????? ????? ??????????? ??? ??????????? ??????????? ?? ????? ? ?????????????? ????. ? ???????? ???????????? ?????? ?? ????? ???? ? ??????: ?? ??????????? Datsun On-Do ?? ???????? Skoda Rapid ? ?????????????? ???????? ???????. ??? ?????????? ?????????? ??? ??????, ??? ?????? ??????? ??????????? ??????? ? ???????. ?????????? ?????? ??????????? ????? ?? ????? https://auto-arenda-anapa.ru/nashi-avto/ ??? ??????? ?????????? ???? ? ???????. ?????????????? ????????? ?????????? ??????? ??????? ????????? ??????? ??? ?????? ???????.
Nomad Cars https://nomadcars.net/ — ??? ???????? ??????? ? ??????? ???? ?? ?????. ?????????? ?????????? ???????? ? ??????? ? ????????? ? ????? ????? ????! ?????????? ???????, ??????? ???? ? ?????? ????????????? ??????.
?????????????????? ????????????? plazmennyy-sterilizator.ru .
?????? ??????
IdeaNavigator – Clear tips and examples, perfect for starting new projects today.
?? ????? ?????? ?? ?????
VelocityMap.org – Guidance is precise, helps create forward motion in daily tasks.
ConstructorPoint – Well-structured content, helping users understand ideas quickly.
???????? Noblelift Equipment JSC Ltd. ??????????????? ???? ??? ??????? ????? ?? ???????????? ????????? ??????? ? ?????? ????????? ????? ???????????? ??? ????????????? ?????. ?????????? ????????????????? https://nobleliftrussia.ru ????????? ??????? ??????????? ???????????, ??????????, ??????? ? ????????? ??????? ? ??????????? ????????? ?? 36 ???????. ???????????? ????????????? ????????????? ?????????? EAC, CE ? ISO 9001, ???????????? ? ????? ??? ??? ????????????, ???????????? ??????????????? ?????????? ? ????????.
???? Xrumer ???????? xrumer 23 strong ai ????????
GrowthSteps – Clear messaging, shows growth paths in a practical way.
?????? login
AlignFlow – Easy-to-follow structure, navigation feels natural and efficient.
Everything posted was actually very reasonable. However, think about this, what if you were to create a awesome post title? I ain’t saying your content isn’t good., however what if you added a headline that grabbed a person’s attention? I mean %BLOG_TITLE% is a little vanilla. You might look at Yahoo’s home page and note how they create news titles to get viewers to open the links. You might add a related video or a picture or two to get people excited about everything’ve got to say. Just my opinion, it could bring your blog a little livelier.
??????? ????? ?????? ? ????????????
kraken ????
xrumer ???????? ???????? ???? Xrumer 19
? ???????????? ????? ??????? ???????? ??????? ????? “??? ????”, ??? ??????????? ???????? ????? ???????? ????????? ???????? ? ornamental??? ???????, ????????? ??????????????? ? ????????????? ???????. ? ???????????? ??????? ??????, ?????, ?????, ?????, ???? ????????? ????????????? ??????? ? ???????????? ????, ??? ?????????? ? ??????? ? ????????? ???????? ??????. ?????? ????? ???????? ???????????: ??????, ?????????, ????????, ?????????, ? ????? ornamental??? ?????????, ????, ??????? ? ?????, ????? 500 ????? ?? ???????? ????????????? ??????????????. ??????????? ? ?????? ???????? ????????????, ?????? ???????? ? ???????, ???????????? ???????? ???????? ?? ??????????????? ?????. ???????? https://sadovodklin.ru/ ????? ???????????? ? ?????????, ??????? ? ???????, ??? ??????? ???????? ?? ????? ?? ????? ? ??????? ???????? ?????? ??????, ? ???????? ????? ????? ?????? ??? ?? ???????? ??? ??????????.
TeamAlignmentGuide.net – Helps everyone stay on the same page and work toward shared goals.
kraken ????? ??????????
SignalFlow – Easy-to-follow content, finding information is quick and intuitive.
Glassway — ??????? ????????????? ????????? ????????, ??????????? ???????????, ???????????? ???????????? ? ??????? ?????? ??? ???????????? ? ??????? ???????????. ???????? ?????????? ?????? ????: ?? ?????????????? ?? ???????, ??????? ? ??????????, ????????, ????????????? ?????????, ??????????? ? ?????????? ?????????????. ???????????? ? ??????????, ????????? ? ???????? ???????????? ?????? ?? https://glassway.group — ????? ??????? ??????? ??? ????????, ???????????? ? ??????? ???????? ? ???????? ?? ???????? ? ?????.
ClarityMomentum.io – Sparks creative thinking while remaining actionable and straightforward.
kraken login
???? ?????? 23 ??? ???????? xrumer 5.0 platinum
ClarityLab – Helpful explanations and clear layout simplify strategy planning.
kraken darknet tor
kraken ????? ??????????
?????? ??????? ???????
??????????? ????? “?????? ????” ? ???????? ????????????? ????????????????? ?????? ??? ????? ? ???????? ? ?????? ??????????????? ??????? ?? ???. https://kinder-dent-lyubertsy.ru/ ?????????? ?????? ?????? ?????: ?? ???????????????? ??????? ? ??????? ??????? ?? ???????????, ?????????????? ? ??????????. ????? ??????????? ???????? ????????, ? ??? ????? ???????? Vector ??? ??????????????????? ????????. ????? ????? ????? ??????????? ??????, ?????????? ???? ?? ???????? ????????. ???????? ????????? ??????????? ?????, ????????? ???????, ??????? ? ????????? ??????????????, ???????????? ? ???????? All-on-4/6.
FocusFlow.io – Encourages productive routines and smooth task management.
BTB Connect — ???????????? ??????? ?????? ? ???????? ??????? https://btbconnect.ru/ – ???????? ????????? ??? ?????????? ? ??????????????? ?????-???????. ?????? ???????????? ?? ????????, ??????? ???? ????? ??????? ???????? ??????????????, ????????? ? ???????? ???????????. BTB Connect ?????????? ?????? ? ?????????????? ????????, ???????? ?????? ??? ??????????? ????? ? ??????????????.
OperationsDesk – Helpful guides and smooth interface make navigating easy.
?????? ????? ??????????
EngineDesk – Helpful guides, layout makes learning concepts fast and simple.
?????? ??????????? ????
xrumer ??????????? ???? ???? xrumer ????????
kraken market
??????????? ?????
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
?????? darknet
MotionLab – Clear and concise instructions make understanding the material effortless.
kraken ????
kraken ???????
xrumer ??????????? ???? ???????? xrumer
DriveDock – Easy-to-follow content, executing tasks feels simple and natural.
kraken ??????
kraken tor ???????
kraken link
https://t.me/s/kAzINO_s_MInIMALNYm_DEpOzIToM/4
kraken darknet market
IntentDockPro – Well-structured resources and easy-to-follow steps make the site effortless to use.
?????? ????? ?????? ????? .
???????? ????? ? ??? ?? ????????????? http://www.kuhni-na-zakaz-4.ru .
?????? ???????? ??????????? ???? dsn-ofitsialnyj-sajt.ru .
??????????? ???????? ??????? ?? ?????? ??????????, ?? ? ?????????? ???????, ???????? ????? ???? ???? ? ?????????? ? ?????????? ?????????? ??? ?????????????? ?????? ????????????. ??????? ??????? ?? ???????? ? ????? ????????? ???????????? ????????? ?????????????, ???????????? ? ???????? ? ???????????? ???????????? ????????? — ?? ???????????? ?? ??????????? ?????? ? ????????? ???????? ??????. ????????????? ???????? ?????????? ??????? ????????? ?????????? ?????? ??????? ???? ? Cesal, ?????????? ??? ??????????? ???????? ??? ??????????????? ????????? ??? ??????????? ????????????. ?? ????? https://potolki-52.ru/ ???????? ??????? ??????????? ??? ??????? ????????? ??? ?????????? ??????? ?????????, ? ????? ????????? ???????? ????????????? ? ????????? ???????. ??????????? ??????????? ?????? ?? ???? ?? ?????? ??????????? ????????? ???????????? ??????????? ??? ????? ??????????? ??????? ???????? ??? ???????????.
????? ?????? ???? ?????? ? ?????? ???????? ???? https://bs-service.com.ua/ – ??? ?? ??????? ?????? ???????????????? ?????? ?? ??????? ?????????????, ? ????? ?? ???????????? ???????????. ??????? ???? ??????????????? ???? ?? ?????, ????? ???????? ?????? ?? ???????????? BS Service.
????? ??????? ????? ? ???????? ????????? ??????? ????? “??????” sakura-pitomnik.ru ?????????? ???????????? ??????? ??????? ? ?????????? ????????, ???????????? ??????????, ????, ???????????? ? ???????????? ?????? ?? ?????? ?????????? ?????? ? ??????. ???????? ???????????? ???????? ???????? ?? ?????-?????????? ? ????????????? ???????, ???????? ??????????? ?????? ?? ?????????? ? ??????????????? ???????? ? ????????? ?????????? ???????????? ???????. ??????????? ????????? ???????????? ???????????????? ?????? ???????? ? ????????? ?????? ?? ?? ??????????? ?????.
????? ????????? ??? ??????? ??????, ????????????? ? ???????? ???????? ???? https://xn--80abutqu5e.xn--p1ai/ – ???????????? ? ????? ???????????? ?????????, ? ??????? ?? ??????? ??? ??????????? ??? ??? ????????? ? ???????? ? ??????? ????????? ?????? ??????? ? ????? ???????. ???????? ? ??????????? ? ???????????? ??????. ????????? ?? ?????.
??? ?????? ???????? ??????????? dsn-ofitsialnyj-sajt.ru .
?????? ????? ?????? ????? .
?????? ??? ????? ??? ?? ????????????? kuhni-na-zakaz-4.ru .
??? ????? ??????? kraken
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
??????? ?????? ??????????? ??????? ?????? ??????????? .
?????? ????? ?? ????? ??? kuhni-na-zakaz-5.ru .
????? ?? ????? ???????????? ??? http://www.kuhni-na-zakaz-4.ru/ .
????? ????? ??? http://www.kuhni-na-zakaz-5.ru/ .
??????? ?????? ?????? ???????? ??????????? ofitsialnyj-sajt-dn-2.ru .
?????? ?????? ?????? ?????? .
??? ?????? ???????? ?????? ??????????? fen-d-11.ru .
dyson ?????? ??????????? dn-kupit-2.ru .
?????? ?????? ??????????? ofitsialnyj-sajt-dn-1.ru .
?????? ??????????? ????????? ?????? ??????????? ????????? .
https://1wins34-tos.top
dyson shop ofitsialnyj-sajt-dn.ru .
????? ????? ??? kuhni-na-zakaz-4.ru .
?????? ?????? ??????????? ofitsialnyj-sajt-dn-2.ru .
????????? ??? ????? https://utgardtv.com IPTV???????, ????????? ?????????? ??? ???????? ?? ??? ? ??????! ????? 2900+ ??????????? ? ??????? ???????? (HD / UHD / 4K). ?????? ?? ????????: ??????, ???????, ????????, ??????, ??????, ????. ??????, ?????, ??????, ????, ??????????????. ????????? ????? 18+
?????? ?????? ??????? ??? ????? ??????????? ???? ???? ? ????????… fen-d-11.ru .
https://wokerman.ru
??????? dyson ?????? ??????? dyson ?????? .
dyson ??????? ? ??? dyson ??????? ? ??? .
??? ?????? ???????? ??????????? dn-kupit-2.ru .
????? ??????? ??????? ?????? ? ??3 ?????????? ?????, ????? ??????, ????????? ?? ?????? ? ??????????. ??????? ?????, ????? ?? ???????????? ? ????????, ?????????? ???????? ?????. ????????? ?????? ? ????? ?????.
?????? ??????????? ???? ?????? ?????? ofitsialnyj-sajt-dn.ru .
Let me share with you something the majority of septic companies will not: there are two types of people in this reality. Those who believe septic systems are merely “underground boxes for waste,” and those who’ve had raw sewage bubbling into their property at 2 AM. I learned this reality the difficult way in 2005—knee-deep in mud, shivering in a Washington deluge, as my siblings and I assisted a weathered installer repair our family’s failed system. I was a teenager. My hands blistered. My jeans were ruined. But that night, something changed: This isn’t just manual labor. It’s families’ lives we are protecting.
This is the dirty truth: the majority of septic companies just pump tanks. They act like band-aid salesmen at a chainsaw convention. But Septic Solutions? They are different. It all started back in the early 2000s when Art and his siblings—just kids scarcely tall enough to lift a shovel—helped install their family’s septic system alongside a grizzled pro. Imagine this: three youngsters knee-deep in Pennsylvania clay, understanding how soil porosity affects drainage while their peers played Xbox. “We didn’t just dig trenches,” Art explained to me last winter, steaming coffee cup in hand. “We understood how soil whispers secrets. A patch of marsh plants here? That’s Mother Nature screaming ‘high water table.'”
https://charlierolt530.trexgame.net/what-makes-septic-certification-a-trust-signal-for-homeowners
?????? ??????? ??? ????? ??????????? ???? ? ????????? ?????? ???… fen-d-11.ru .
?????? ?????? ??????????? ?????? ?????? ??????????? .
?????? Kra47.at
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
controlmomentum – Shows how maintaining oversight while advancing projects ensures reliable progress.
Visit Site – Layout is crisp, browsing is easy, and content feels trustworthy and clear.
conceptflow – Encourages keeping ideas on track with a clear structure for action.
dyson ??????? ?????? dn-kupit-2.ru .
dyson ??????? ???????? ofitsialnyj-sajt-dn-1.ru .
?????? ??????????? ???? ?????? ?????? ?????? ??????????? ???? ?????? ?????? .
Allow me to tell you something nearly all septic companies won’t: there are two types of people in this life. Those who assume septic systems are just “underground boxes for waste,” and those who have had raw sewage bubbling into their backyard at 2 AM. I discovered this reality the difficult way in 2005—standing in muck, shivering in a Washington downpour, as my family and I aided a weathered installer fix our family’s broken system. I was fourteen. My hands were raw. My clothes were wrecked. But that evening, something crystallized: This isn’t just digging. It’s people’s lives we’re preserving.
Let me share the ugly truth: the majority of septic companies just maintain tanks. They are like quick-fix salesmen at a disaster convention. But Septic Solutions? They are unique. It all originated back in the beginning of the 2000s when Art and his siblings—just kids scarcely tall enough to lift a shovel—helped install their family’s septic system alongside a grizzled pro. Imagine this: three pre-teens buried in Pennsylvania clay, discovering how soil porosity affects drainage while their buddies played Xbox. “We didn’t just dig trenches,” Art told me last winter, hot coffee cup in hand. “We discovered how soil whispers secrets. A patch of wetland vegetation here? That’s Mother Nature yelling ‘high water table.'”
https://writeablog.net/tronenrjto/the-connection-between-septic-certification-and-long-term-property-value
????? ?? ????? ? ??? ???? ????? ?? ????? ? ??? ???? .
directionengine – Highlights how clarity helps navigate projects efficiently and creatively.
?????? ?????? ??????????? ofitsialnyj-sajt-dn.ru .
need a video? milan production house offering full-cycle services: concept, scripting, filming, editing and post-production. Commercials, corporate videos, social media content and branded storytelling. Professional crew, modern equipment and a creative approach tailored to your goals.
?????? ??????? ??? ????? ? ????????? ???? ??????????? ???? ?????… fen-d-11.ru .
??????????? ???? ?????? ????????? ofitsialnyj-sajt-dn-2.ru .
conceptclarity – Highlights the importance of clarity in moving ideas into actionable steps.
energypilot – Encourages guiding your attention to generate maximum results.
?????? ???????? ?????? dn-kupit-2.ru .
Exeed ? ??? ? ???????????? ?????? ??? https://exeed-iat.ru/ – ??? ???????? ???? ? ???? ? ???????, ? ????? ???????????????? ??????. ??????? ?? ????? ????????? ???, ???? ???????????? ? ???????????. ????, ???????????? ? ????????? ??? ?? ?????, ? ????? ??????????? ?????????? ?????????, ?????-??, ??????, ?????? ? ?????, ????-?????!
??? ??????? ???? ??? ??????? ????: ????? ??? ???, ??? ????? ?????????? ? ??????? ?? ??????????. ?????????????? ??????? ??????? ??????????? ???????? ?????????? ???????????, ???????? ? ??????? ????????. ??? ??????? ? ???? ?????????? ?????????? ?????, ????????????? ???????? ? ??????? ??????? ????????????, ??? ?????? ??? ???????? ????????? ??? ???????????, ?????, ??????? ? ?????? ??????????? ?? ???????. ?????? ???????? ???? ??????????? ??? ?????????? ????, ??????? ??????????? ??????? ???????????? ? ???????????. ??? ??????? ? ???? – ??? ?????????? ? ???? ??????? ???????????? ? ??????????? ?? ????? ??????.
?????? ?????????? ???????? ?? ??????: ?????, ??? ? ?????? ??????? ??? ????? ??????!
???? ??????? ???? ??????
progresspilot – Shows how guiding tasks clearly ensures reliable forward movement.
https://agritown-kusano.jp/ ?????????????????????????????????????????????????????????????????????????????
?????? ????? ?? ????? ? ??? ?????? ????? ?? ????? ? ??? .
?????? ??????? kra46.at
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
dyson ???????? ?????? ofitsialnyj-sajt-dsn.ru .
dyson ??????? ?????? ???????? ofitsialnyj-sajt-dn-1.ru .
???????? ????? ??????? ??????????? ????????????????? ?????, ???????? ????? ???? ???? ? ????? ? ????????? ? ?????????? ????????????. ??????? “?????? ????” ? ?????? ?????????? ???????????????? ?? ???????? ???????????? ? ???????????? ??????? ??? ???????? ??? ????????????? ???????? ?????????. ??????????? ???????????? ? ????????????????? ????? ???????????? ?????????? ?????????? ???????? ????? ?????????: ?? ???????????????? ??????? ??????? ??? ?? ??????????? ?????. ??????? ?????? ?? ????? https://kinder-dent.ru/ ??? ??????????? ?????? ?????? ????? ??? ????? ? ????????, ??????? ??????????, ???????????? ???????????? ? ?????????????? ??????????? ????? ?? ?????? ????? ?? ???? ?????. ?????????? ???????????? ???????????? ??????? ????????? ?????????????? ???? ???????.
??? ??????? ???? ??? ??????? ? ????: ????? ???, ??? ????? ??????????, ???????????? ? ???????. ???? ?????????? ???????? ? ???? ??????????? ??????????? ???? ? ??????????? ??????????, ????? ??? ????????? ??? ????? ?????? ??????? ????????????. ?????????????? ??????? ??????? ??????????? ???????? ??????????, ???????? ? ???????? ?????????? ? ?????????? ???????, ???????? ???????? ??????????????? ?? ?????? ? ???????????? ????????. ??? ??????? ? ???? – ??? ?????????? ?????, ????????????? ????????, ?????? ??????????? ? ???????????? ???????, ??? ??????????? ??????????? ?? ????? ???????. ??? ??? ???????? ??????? ? ????? ???????????, ???? ?? ??????? ?? ???????, ????? ??? ?????? ???????? ????? ?? ???????. ? ??? ??????? ???? ?? ??????? ???????? ????? ?????? ? ??????? ??? ???? ????? ?????????.
?????? ????????????? ???????? ?????????? ?????? ??????? ?????? ????? ???????, ?????? ??? ?????????. ???????? ????? ? ?????, ??????? ?? ?????? ? ?????????, ??????????? ? ??????? ?????. ????????? ??? ?????? ??????????? ? ??????? ?????.
I need to tell you something most septic companies refuse to: there are two categories of people in this world. Those who think septic systems are just “subterranean tanks for waste,” and those who have had raw sewage gurgling into their yard at 2 AM. I learned this distinction the tough way in 2005—standing in mud, freezing in a Washington deluge, as my siblings and I assisted a grizzled installer fix our family’s collapsed system. I was fourteen. My hands blistered. My pants were ruined. But that evening, something crystallized: This isn’t just manual labor. It’s people’s lives we are preserving.
Here’s the harsh truth: nearly all septic companies just maintain tanks. They act like quick-fix salesmen at a disaster convention. But Septic Solutions? These guys are special. It all originated back in the beginning of the 2000s when Art and his family—just kids barely tall enough to lift a shovel—aided install their family’s septic system alongside a experienced pro. Imagine this: three pre-teens waist-deep in Pennsylvania clay, understanding how soil permeability affects drainage while their friends played Xbox. “We never just dig ditches,” Art told me last winter, hot coffee cup in hand. “We learned how soil whispers mysteries. A patch of cattails here? That’s Mother Nature yelling ‘high water table.'”
https://ameblo.jp/milotebr728/entry-12951537727.html
?????? ???????????? ???? ? ?????????????? ???????? ? ?????? ???????????? ?????? Rosseriaall ?????????? ???????? ????????? ?????????? ???????? ??? ??????????? ??????-????????? ? ????? ??????? ?????. ??????? ???????? ??????? 2025 ???? ? ??????????? ???????? ???????, ????????????????? ?? ??????: ?????????, ?????????, ???????????? ???????, ??????? ?????, ??????? ? ???????? ???????. ?? ????? https://rosseriaall.net/ ?? ??????? ??? ?????????? ????????????? ??????? ????? “????? ?????????”, ??? ? ?????? ???????? ???????? ????. ??????? ????????? ????????? ?????? ????????? ??????? ?? ??????????, ? ?????????? ?????????? ??????????? ?????? ? ????? ?????????? ??????? ?????????????? ???????????.
???????? ?? ?????? ??????? ? ??????? ?? ?????: ????? ?????? ? ?????????? ??????? ??? ???????? ??????.
??????? ????? ????? https://uroki-vokala-moskva.ru
??????? ?????? ???? https://ploskaya-krovlya-moskva.ru
???????????? ??????? dyson ofitsialnyj-sajt-dn.ru .
?????? selector casino ?????????????? ?????????????.
????? ?????? ???????? ????.
????? ??????????? ????????????? ???????.
????????????? ??????? — ????? ????????? ????????.
???????? ???????????? ? ????????? https://mor-produkt.ru
???? ??? ???? https://dacha-ua.com ? ???????: ??? ? ?????, ???????? ???????? 2026, ??????????? ??????, ???? ? ??????, ?????? ?? ???????, ??????? ?? ?????? ??????, ??????????? ??????, ??????????? ? ???????????. ????????? ?????? ?? ??????????.
Omnigram https://omnigram.ru/ — CRM ? ?????????: ???????? ??????? ?? WhatsApp, Avito, Telegram-?????, Gmail ? ?????? ??????? ????? ? Telegram-?????? ? ???????? ?? ????????. ??????? ???????? ??????, ?????? ?????????? ???????, ?????? ??????? ?????? ????????? (/paid, /closed), ?????????? ??-????????? ? ???????/API. ????? — ?? ???? ????? (QR). ????? ?? 1000 ?/???: 5 000 ????????? ? 1 ???; ?????? — pay-as-you-go. ???????? ?? ????? ??????????, ?????? ????? ????????????.
????? ?????????? ????????? ?? ????? ?????? ???????? ?????? ?? ????? ?????????? ? ??????? ????????. ?????? ??????? ? ???????, ??????? ??????, ??????????? ??????. ??????? ? ???????, ??????? ?????? ? ????????. ???????? ??? ??????? ? ???????? ???????
?????? ?????????? ????????? ???????? ??????? ?????????????? ??????, ??????????? ?????? ? ?????????? ??????. ??????? ????? ???????? ? ??????????, ?????? ? ????????. ??????? ???????????? ? ????????
???????????? ???? ??????? ????????????????? ??????? ? ??????????????, ?????????? ? ???????????? ???????????? ????????. ???????? ????? ???????????????? ?? ???????? ????????????? ???????? ??? ???????, ???????????????? ????? ? ????????????? ??????????. ?????????? ???????? ???? ??????????? ??????????? ???????? ? ????????? ???????????????? ?????????????? ?????? ????. ??????????? ????????? ?????? ? ????????? ?? ???? ???, ????????? ????????????????? ????????? ???????????? ????????. ????????? ?? ??????? ? ??????????? ????? ?????? ?? ????? https://mvpol.ru/ ? ??????? ????????. ?????????? ????? ???????? ? ??????????? ????? ???????? ????? ???????????? ?????? ?????????????.
????? ?? ????? ????? ?? ????? .
???????? ?? ?????? ???????????? ??????? — ??? ???????????, ???????????? ?????? ?? ?????????? ???? ?? ????????? ???????, ? ???????? ??????????. ??? ????????????? ???????????? ?? ??????, ????????? ?????? ? ??????????? ????????. ???????????? ??????? ??????????? ?? ?????? ??????????: ?????????, ???????????? ???? ?????? ? ??????? ???????, ????????????, ???????? ????????????? ????? ??? ??????????, ??????? ??????? ? ?????, ???????? ?????? ????????? ? ??????? ?????/?????? ???????. ??? ?????? ???????????? ??????? ??????? ???????? ???????? ?? ??????? ????????, ?????? ?????? ?????????????, ???????? ?????? ? ?????? ?? ??????. ????? ????? ???????????? ? ????????? ?????? ???????, ????? ???????? ????????????? ? ??????????. ??????????? ????? ????????????? ????????? ??????, ??????? ??? ????????? ?????????? ????????? ????? ? ?????? ??? ??????????? ????? ???????? ? ????????? ??????.
https://wokerman.ru/
I need to explain something nearly all septic companies will not: there are two types of people in this world. Those who think septic systems are simply “underground boxes for waste,” and those who have had raw sewage erupting into their yard at 2 AM. I discovered this distinction the difficult way in 2005—waist-deep in sludge, shivering in a Washington deluge, as my family and I aided a weathered installer fix our family’s collapsed system. I was 14. My hands ached. My pants were wrecked. But that night, something changed: This ain’t just digging. It’s families’ lives we’re safeguarding.
Let me share the harsh truth: most septic companies just maintain tanks. They’re like band-aid salesmen at a chainsaw convention. But Septic Solutions? They’re different. It all originated back in the beginning of the 2000s when Art and his brothers—just kids hardly tall enough to carry a shovel—assisted install their family’s septic system alongside a grizzled pro. Visualize this: three youngsters waist-deep in Pennsylvania clay, discovering how soil absorption affects drainage while their buddies played Xbox. “We didn’t just dig trenches,” Art explained to me last winter, warm coffee cup in hand. “We understood how ground whispers truths. A patch of wetland vegetation here? That’s Mother Nature yelling ‘high water table.'”
https://unsplash.com/@hafgarxfja
?????-????? ? ????????? ? ??? Gentalion https://gentalion.ru/ ? ????? ??????????? ? ?????? ?????? – ??? ???????? ? ?????????? ??????, ???????????? ?????? ? ??????????? ?????????????? ?????????! ??? ????? ?????? ? ?????????? ????????????? ???????: ?????? ??????, ???????? ??????, ????????????? ???????. ???????, ?????????? ? ?????? ? ???????? ??????? ??? ? ??? ? ??????!
??? IT-?????? https://nashkomp.ru/ – ??? ????????? ? ???? ??????? ??????????. ????????? ????????? ?????????? ??????? ?? ????? ?????????, ?????? ??????? ?????? ? ????? ???????? ????????. ?? ????? ?? ??????? ????????? ????? ???????????? ???????????, ???????????? ??????????? ?? ???????????????? ? ?????? ?? ?????????????????. ?? ????? ?????? ? ???????: ?? ??????????? ?????????? ?? ?????? ???????? ??. ???? ???? — ??????? ?????????? ?????????? ??? ?????????????? ? ???????????. ?????? ? ????? ???????? ??????? ?????? ? ????!
?????? ?????? ? ?????? ???????? stajler-d-11.ru .
?????????? ???????????? ?????????? ??? ????????? ?????? ??????????? ????????? ????????? ????????? ????????, ????????? ? ??????? ????????????? ???????? ? ????????? ??????? ????????, ??? ???????? ????? ??? ????????? ??????? ? ?????. ???????? Novatex ?? ????????????? ???????????????? ?? ??????? ?????????????? ?????? ? ??????????, ????????????? ? ?????? ?????????? ?????????????? ? ??????????? outdoor-??????????? — ?? ???????? ? ?????? ?? ??????????? ??????? ????? 7.62, ?????????????? ???????? ?????? ? ????????????? ????????. ?? ??????? https://nova-tex.ru/ ??????????? ??????? ??????????? ???????: ??????????, ????????? ?????????, ???????, ???????, ???????? ????? ? ??????????, ??????????? ??? ??????????? ?????????? ?? ??????? ? ????? ????? ????. ??????? ??????? ???????? ?????????? ????? ?????????? ??????? ?????? ?? ???????????? ?? ????????????, ? ??????????? ?????? ??????? ?????? ??????? ????????????? ?????????? ????????? ???????, ??? ????? ?????????? ????????????? ??????? ? ????????? ? ??????????? ?????? ?? ???????.
?????? ??????? ??? ????? ?????? ???? ??????????? ???? ? ????????… fen-d-12.ru .
????????_??????? ??????????????: ?????? ??? ??????
?????? selector casino ??????? ??????? ????????.
?? ???? ????? ?????? ???????????????.
????????? ??? ??????? ?????????.
????????????? ????????? — ??? ????????? ?????????.
???. ?? ???. ???? ???? ???: ????? ????? ??? ” ? ?????????? ????? ??????. ??????? ???, ??? ??? ????? ???? ??. ????? ??? ????? ?? ?? ????? ???? ????? ??? ??? ?????? ?????? ???? ?????. ??????, ?????? ??????? ??????? ?????? ???. “??, ????,” ??? ?????? ?????? ????? ??, ??? ???? ??? ?? ?????? ????? ???? ??????? ??????. ?? ??? ???? ??? ?? ?? ????? ??? ??? ?????? ????, vertexcentury.com
??????? ??????? https://faamru.com ?????????????? ??????? ??? ???????? ???????????, ?????????, ?????????????? ? ??????????. ??????? ??? ??????????? ????????? ??????: ?????????? ????????, ?????? ??????, ???????? ?????? ? ??????? ??????, ?????? ? ???????? ??? ?? ?????????? ??????? ? ??????????? ???????? ??? ??????
????? ?? ????? ??? ???????? ? ?????? http://kuhni-na-zakaz-5.ru/ .
??????? ?????? ?????? ??????????? ???? stajler-d-11.ru .
?????? ??? ?????? ???????? ? ?????? ??????????? ???? ?????? ??? ?????? ???????? ? ?????? ??????????? ???? .
?????????? ????????????????: ???????? ? ???????
??????? ??????? https://ab-resurs.ru ?????????????? ??????? ??? ???????? ??????????? ? ??????????. ???????? ??????? ??? ?????????? ?????? ????????? ???????: ??????? ????? ???, ???????????????? ?????? ?? ??????????, ???????????? ????????????, ???????? ? ??????????? ???????? ??? ??????? ? ??????????? ?? ???? ??????
Here’s the harsh truth: most HVAC failures occur because someone missed a step. Didn’t calculate the load correctly. Used incorrect equipment. Got wrong the insulation needs. We have fixed hundreds of these messes. And every time, we record another insight. Like in 2017, when we decided on adding remote monitoring to each install. Why? Because Sarah, our senior tech, got tired of watching homeowners lose money on bad temperature settings. Now clients save $500+ yearly.
https://community.cisco.com/t5/user/viewprofilepage/user-id/1951244
?? ????? ??????
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
????????????? ???????? ????????????? ????????: ?????????? ? ??????????.
??????? ??????? https://faamru.com ?????????????? ??????? ??? ???????? ???????????, ?????????, ?????????????? ? ??????????. ??????? ??? ??????????? ????????? ??????: ?????????? ????????, ?????? ??????, ???????? ?????? ? ??????? ??????, ?????? ? ???????? ??? ?? ?????????? ??????? ? ??????????? ???????? ??? ??????
?? ????? ?? ?????
??????? ?????? ??? ????? ? ????????? ?????? ??????????? ???? ???… ??????? ?????? ??? ????? ? ????????? ?????? ??????????? ???? ???… .
????????? ??????? ?????? ?? ?????????? https://ustrojstvo-ploskoj-krovli.ru
??????? ??????? https://ab-resurs.ru ?????????????? ??????? ??? ???????? ??????????? ? ??????????. ???????? ??????? ??? ?????????? ?????? ????????? ???????: ??????? ????? ???, ???????????????? ?????? ?? ??????????, ???????????? ????????????, ???????? ? ??????????? ???????? ??? ??????? ? ??????????? ?? ???? ??????
???????? ???? https://strong.by/ ? ?? ??????? ?????? ????? ? ?/? ???????? ? ??????? ? ??????. ? ??? ??????? ????? ??????????? ????? ?? ??????, ??? ??? ?? ??? ??????? ??????? ???????????? ???????? ?? ???????? ???? ??? ?????? ???? ? ???. ?????? ????????? ????? ????, ? ?? ??????? ??? ??? ????????. ????????? ???????? ?????????????? ??? ?????????????? ????????? ???? ? ???? ?? ??????.
??????? ??? ????? ?????? ???? ? ????????? ??????????? ???? ?????… ??????? ??? ????? ?????? ???? ? ????????? ??????????? ???? ?????… .
????? ? ?????????? ??????? ??????? ??????? — ????? ????? ?????, ??? ????? ???????????? ????? ?? ????. ????? ? ??????? ?? ??????? ????????????? ????? ?????????? ?????? ????????? ????? ???????????? ??????? ? ???????? ?????????????. ????? ???????? ?????? ? ?????? ?? ??????, ???????? ?????? ?????????? ?????? ? ??????? ??? ??????? ???????. ????????? ??????? ????????? ? ?????????? ??????????? — ????????? ????????? ??????????? ??????? ? ????????. ????????? ?? ??????? ? ?????????? ????? ????? ?????? ?? https://sauna-koptevo.ru/ ????? ????????????? ???????. ????????? ??????? ? ?????????? ?????????? ???? ??????????? ?????????? ????? ??? ???????? ?? ????? ???????.
????? ??????? ?????? ? ?????? xakerforum.com/threads/uslugi-xakera-vzlom-tajnaja-slezhka.282/page-6 — ??? ???????????? ?????? ??? ???, ??? ???????? ????????? ? ?????????????????, ??????????? ? ??????????? ???????? ????????????. ????? ?????????? ????????????????? ??????? ?? ?????? ??????, ???????????? ?? ?????????????, ???????? ???????????, ?????????? ????? ? ???????, ? ????? ?????? ???????????? ?????? ????? ??????????????? ? ?????????. ????????? ????????? ??????????, ?????????? ?????? ? ??????????? ??????? ???????????? ???????? ????????????????? ??????????, ????? ?????? ?????? ? ?????????? ??????. ?? ?????? ?????????? ?????? ????????????, ????????? ?????? ???????? ?????? ? ??????????? ?? ???????? ???????.
?????? iPhone 17 https://itcrumbs.ru/neochevidnye-pomoshhniki-10-skrytyh-funktsij-iphone-17-kotorye-sekonomyat-vam-vremya_105144 ????? ?????? Apple ? ??????????? ????????, ??????? ??????????????????? ? ?????????? ???????. ???????????? ???????, ????????, ???????? ????????? ??????. ????? ???????????? ??????, ??????? ?????? ? ??????? ????????.
?????? ???????? https://qckl.net/servers.html ? ????????? ????????????: ?????? ????????????, ??????? ???????? ???? ? ???????? ???????? ??????. ?????????????? ???????, ????????? ??????????? ? ????????? 24/7. ?????????? ??? ??????? ? IT-????????.
????? ????? ?????? ???? ? ????????? ?????? ?? ?????, ??????? ? ???????? ????????????, ???????? ??????????? ???????. ?????? ? ???????? ? ???????, ?????? ? ??????.
?????? ??? ?????? ??????????? ?????? ??? ?????? ??????????? .
This is the harsh truth: most HVAC failures happen because someone ignored a step. Did not calculate the load properly. Used undersized equipment. Miscalculated the insulation needs. We’ve personally fixed countless of these disasters. And each and every time, we record another lesson. Like in 2017, when we decided on adding smart thermostats to all install. Why? Because Sarah, our lead tech, got tired of watching homeowners waste money on inefficient temperature settings. Now clients save $500+ yearly.
https://openlibrary.org/people/productairheating/lists/OL317070L/Product_Air_Heating
??????? ??????????????? ??????????? https://geotekhnicheskij-monitoring-zdanij.ru
?????? ??? ?????? ??????? ???????????? ?????????? ????????????, ?????? ? ????????? ??? Roblox — ? ?? ??????? ????? ????????? ????????, ???????? ????? ??????? ? ????????????? ????. ?? ????? ??????? ??????? https://joyverse.ru/ ????????? ??????????? ?????? ???????, ???? ? ?????? ?? ???? ???????, ??????? ????? ??????????? ??? ????????, ??? ? ??????? ???????.
??????????? ???? ? ?????? ????? ???????????? ??????????? ???? – ??? ?????????? ? ???????, ????? ? ??????????????????? ?????? ????. ? ??????, ? ???????? ????????????? ???????, ??? ???????? ?????????. ???????? Okna Service ?????????? ??????? ??????????? ??????????? ????, ?????????? ????? ??????? ?????????? ????????. Okna Service ?????????? ?????? ??????????? ?????????? ??????? ?? ??????? ??????????????. ??? ??????????? ?????????????, ???????????? ? ????????? ?????????? ? ???????? ?????????????. ?? ?????? ??????? ???? ? ????????? ???????? ???????, ??????????? ????? ? ?????? ?????????????, ? ??????????? ?? ????? ?????????????? ???????????? ? ???????. ?????? ???????? ?????????, Okna Service ?????????? ????? ???????????????? ???????? ? ?????????. ????????????????? ?????????? ? ??????? ?????? ?????? ??????????? ?????????? ????????? ????, ??? ???????? ?????????? ?????? ??? ??????????? ?? ???????????????? ? ?????????????. ???????????? ?????? ????? ?????? ?? ??? ??? ???????????? ???? ????? ??????? ????. Okna Service ?????????? ?????? ?????? ?????, ??????? ?????, ????????????, ???????? ? ????????? ????. ???????? ????? ????????????? ??????????? ? ??????????????? ????????????. ??? ??????? ????????? ??????????? ??????? ??? ?????? ???? ??? ?????, ???????? ??????????? ??????????? ? ???? ?????? ?????????. ??????? Okna Service, ?? ????????? ??????????, ???????? ? ???????????????. ???????? ???? ??? ??? ???????, ????????? ????? ??????????? ???? ?? Okna Service.
?????? ??????? ??????????? ??????????? ??????? ??????????? ???????? https://razdel-osokn.ru
???? Rehau ?????? ????? ???????????? ??????????? ???? – ??? ?????????? ? ???????, ????? ? ??????????????????? ?????? ????. ? ??????, ? ???????? ????????????? ???????, ??? ???????? ?????????. ???????? Okna Service ?????????? ??????? ??????????? ??????????? ????, ?????????? ????? ??????? ?????????? ????????. Okna Service ?????????? ?????? ??????????? ?????????? ??????? ?? ??????? ??????????????. ??? ??????????? ?????????????, ???????????? ? ????????? ?????????? ? ???????? ?????????????. ?? ?????? ??????? ???? ? ????????? ???????? ???????, ??????????? ????? ? ?????? ?????????????, ? ??????????? ?? ????? ?????????????? ???????????? ? ???????. ?????? ???????? ?????????, Okna Service ?????????? ????? ???????????????? ???????? ? ?????????. ????????????????? ?????????? ? ??????? ?????? ?????? ??????????? ?????????? ????????? ????, ??? ???????? ?????????? ?????? ??? ??????????? ?? ???????????????? ? ?????????????. ???????????? ?????? ????? ?????? ?? ??? ??? ???????????? ???? ????? ??????? ????. Okna Service ?????????? ?????? ?????? ?????, ??????? ?????, ????????????, ???????? ? ????????? ????. ???????? ????? ????????????? ??????????? ? ??????????????? ????????????. ??? ??????? ????????? ??????????? ??????? ??? ?????? ???? ??? ?????, ???????? ??????????? ??????????? ? ???? ?????? ?????????. ??????? Okna Service, ?? ????????? ??????????, ???????? ? ???????????????. ???????? ???? ??? ??? ???????, ????????? ????? ??????????? ???? ?? Okna Service.
Thank you, I’ve just been searching for info approximately this topic for a long time and yours is the best I’ve came upon so far. However, what in regards to the conclusion? Are you sure concerning the supply?
?????? ?????
Let me share with you something most septic companies won’t: there are two kinds of people in this world. Those who believe septic systems are just “buried containers for waste,” and those who have had raw sewage bubbling into their yard at midnight. I understood this difference the difficult way in 2005—standing in muck, trembling in a Washington rainstorm, as my family and I assisted a grizzled installer restore our family’s failed system. I was 14. My hands were raw. My clothes were wrecked. But that moment, something crystallized: This isn’t just dirt work. It’s folks’ lives we are preserving.
Here’s the dirty truth: most septic companies just service tanks. They are like quick-fix salesmen at a chainsaw convention. But Septic Solutions? They’re special. It all started back in the early 2000s when Art and his brothers—just kids barely tall enough to shoulder a shovel—aided install their family’s septic system alongside a grizzled pro. Picture this: three pre-teens knee-deep in Pennsylvania clay, learning how soil permeability affects drainage while their buddies played Xbox. “We did not just dig holes,” Art explained to me last winter, warm coffee cup in hand. “We discovered how soil whispers secrets. A patch of marsh plants here? That’s Mother Nature screaming ‘high water table.'”
https://steemit.com/learn/@sarnalisa/drawing-study-for-septic-tank
?????? ?????? https://riobetcasino-ytr.ru ?????? ?????? ? ????? ? live-??????. ?????? ???????????, ???????, ??????? ????, ????????, ??????? ? ???????? ?????? ???????.
??? ?????? ?????? ??? ?????? ?????? .
Hello, yeah this article is truly fastidious and I have learned lot of things from it concerning blogging. thanks.
????? ??????
??????????? ???????? ???????? ?? ?????? ??????? ? ??????????? ?????????? ? ????????? ???????? ???????????
??????????? ???????? ? ?????????????? ??????????????? ???????? ?????????? ????? ??? ??????????? ? ????? AREON. ?????? ?????? ?????? ????????? ?????????????? ??????????? ????? ?????????? ??????? ? ???????? ???. ?????????? ??????? ????? ?????????? ??????.??? ???????????? ?????????? ??????????????? ? ??????????? ?????? ? ?????????. ??? ??????????? ??????????? ???????, ???????????? ????? ????????? B ? ?????????? ?? ???????????? ?????. ????? ????????? ?????????? ? ??????? ? ???????? ????????? ?? https://parkareon.ru/ ??? ???? ????????. ?????????? ?????? ???????+ ? ?????? ???????? ????? ??????????? ???????????? ???????? ? ?????????????.
???? ? ?????? ? ????????? ????? ???????????? ??????????? ???? – ??? ?????????? ? ???????, ????? ? ??????????????????? ?????? ????. ? ??????, ? ???????? ????????????? ???????, ??? ???????? ?????????. ???????? Okna Service ?????????? ??????? ??????????? ??????????? ????, ?????????? ????? ??????? ?????????? ????????. Okna Service ?????????? ?????? ??????????? ?????????? ??????? ?? ??????? ??????????????. ??? ??????????? ?????????????, ???????????? ? ????????? ?????????? ? ???????? ?????????????. ?? ?????? ??????? ???? ? ????????? ???????? ???????, ??????????? ????? ? ?????? ?????????????, ? ??????????? ?? ????? ?????????????? ???????????? ? ???????. ?????? ???????? ?????????, Okna Service ?????????? ????? ???????????????? ???????? ? ?????????. ????????????????? ?????????? ? ??????? ?????? ?????? ??????????? ?????????? ????????? ????, ??? ???????? ?????????? ?????? ??? ??????????? ?? ???????????????? ? ?????????????. ???????????? ?????? ????? ?????? ?? ??? ??? ???????????? ???? ????? ??????? ????. Okna Service ?????????? ?????? ?????? ?????, ??????? ?????, ????????????, ???????? ? ????????? ????. ???????? ????? ????????????? ??????????? ? ??????????????? ????????????. ??? ??????? ????????? ??????????? ??????? ??? ?????? ???? ??? ?????, ???????? ??????????? ??????????? ? ???? ?????? ?????????. ??????? Okna Service, ?? ????????? ??????????, ???????? ? ???????????????. ???????? ???? ??? ??? ???????, ????????? ????? ??????????? ???? ?? Okna Service.
Hi to all, how is everything, I think every one is getting more from this web site, and your views are fastidious for new viewers.
??????????? leebet
The best reads here: optimieren sie ihre online-pr?senz: die besten ai seo-tools im ?berblick
This is the ugly truth: nearly all HVAC failures take place because someone ignored a step. Didn’t calculate the load accurately. Used cheap equipment. Misjudged the insulation needs. We’ve personally fixed dozens of these failures. And every time, we remember another learning. Like in 2017, when we began adding smart thermostats to each install. Why? Because Sarah, our senior tech, got tired of watching homeowners burn money on bad temperature management. Now clients save 20-30% yearly.
https://www.blinx.biz/product-air-heating
????? ?????????? ???????? ?? ???????????? ??? ????????? ????????? ? ???????? ???????? https://taximinivan54.ru/sheregesh.html ?? ???? ????? ? ??????? ??????? ?? ???????? ????? ???????? ??????????? ???????. ? ??????? ?????????? ??? ???? ???????? ? ??????????? ??????????. ????????, ??? ????????? ? ????? ??????? ????????! ???? ?????????????, ??? ??????. ????? ??????? ?? 7 ?????. ?????????? ?? ???????, ???? ?????? ???? ??????. ?????????? ??? ????, ???? ?????????, ?????? ???? ????????.
?????? ??? ???? ? ?????? ????? ???????????? ??????????? ???? – ??? ?????????? ? ???????, ????? ? ??????????????????? ?????? ????. ? ??????, ? ???????? ????????????? ???????, ??? ???????? ?????????. ???????? Okna Service ?????????? ??????? ??????????? ??????????? ????, ?????????? ????? ??????? ?????????? ????????. Okna Service ?????????? ?????? ??????????? ?????????? ??????? ?? ??????? ??????????????. ??? ??????????? ?????????????, ???????????? ? ????????? ?????????? ? ???????? ?????????????. ?? ?????? ??????? ???? ? ????????? ???????? ???????, ??????????? ????? ? ?????? ?????????????, ? ??????????? ?? ????? ?????????????? ???????????? ? ???????. ?????? ???????? ?????????, Okna Service ?????????? ????? ???????????????? ???????? ? ?????????. ????????????????? ?????????? ? ??????? ?????? ?????? ??????????? ?????????? ????????? ????, ??? ???????? ?????????? ?????? ??? ??????????? ?? ???????????????? ? ?????????????. ???????????? ?????? ????? ?????? ?? ??? ??? ???????????? ???? ????? ??????? ????. Okna Service ?????????? ?????? ?????? ?????, ??????? ?????, ????????????, ???????? ? ????????? ????. ???????? ????? ????????????? ??????????? ? ??????????????? ????????????. ??? ??????? ????????? ??????????? ??????? ??? ?????? ???? ??? ?????, ???????? ??????????? ??????????? ? ???? ?????? ?????????. ??????? Okna Service, ?? ????????? ??????????, ???????? ? ???????????????. ???????? ???? ??? ??? ???????, ????????? ????? ??????????? ???? ?? Okna Service.
Latest Updates: https://fastfoodsegypt.com/2025/05/18/ripper-casino-15-free-chip-best-no-deposit-australia-online-casino-bonus-codes/
???? Rehau ?????? ????? ???????????? ??????????? ???? – ??? ?????????? ? ???????, ????? ? ??????????????????? ?????? ????. ? ??????, ? ???????? ????????????? ???????, ??? ???????? ?????????. ???????? Okna Service ?????????? ??????? ??????????? ??????????? ????, ?????????? ????? ??????? ?????????? ????????. Okna Service ?????????? ?????? ??????????? ?????????? ??????? ?? ??????? ??????????????. ??? ??????????? ?????????????, ???????????? ? ????????? ?????????? ? ???????? ?????????????. ?? ?????? ??????? ???? ? ????????? ???????? ???????, ??????????? ????? ? ?????? ?????????????, ? ??????????? ?? ????? ?????????????? ???????????? ? ???????. ?????? ???????? ?????????, Okna Service ?????????? ????? ???????????????? ???????? ? ?????????. ????????????????? ?????????? ? ??????? ?????? ?????? ??????????? ?????????? ????????? ????, ??? ???????? ?????????? ?????? ??? ??????????? ?? ???????????????? ? ?????????????. ???????????? ?????? ????? ?????? ?? ??? ??? ???????????? ???? ????? ??????? ????. Okna Service ?????????? ?????? ?????? ?????, ??????? ?????, ????????????, ???????? ? ????????? ????. ???????? ????? ????????????? ??????????? ? ??????????????? ????????????. ??? ??????? ????????? ??????????? ??????? ??? ?????? ???? ??? ?????, ???????? ??????????? ??????????? ? ???? ?????? ?????????. ??????? Okna Service, ?? ????????? ??????????, ???????? ? ???????????????. ???????? ???? ??? ??? ???????, ????????? ????? ??????????? ???? ?? Okna Service.
??????? ?????????? ?? ??? https://vrachnadom-sev.ru
This is the harsh truth: the majority of HVAC failures occur because someone missed a step. Failed to calculate the load properly. Used undersized equipment. Misjudged the insulation needs. We’ve personally fixed dozens of these failures. And every time, we remember another learning. Like in 2017, when we decided on adding WiFi controls to all install. Why? Because Sarah, our master tech, got tired of watching homeowners waste money on poor temperature control. Now clients save 20-30% yearly.
https://www.behance.net/productairhea
??????? ?????? ? ??????? ????? kraken ????? ? ??????????? ????????? ? onion ???????? ??? Tor ????????
????????????? ?????????????: ?????? ?? ?????
kraken ????
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
??????????? ??????? ??????? ????????????????? ??????? — ?????? ? ?????????? ??? ?????????? ????? ?????? ??????? ? ?????. ??????? ??????? ???????????? ? ?????????? ?????????? ?????????? ????????? ???????????? ?? ????????, ???????? ? ????????????? ??????. ???????? ???????? ????????? ?????? ???????? ? ????????????? ?????? ???????? ?????????? ???????? ??? ???????. ???????? ???????? ? ?????? ????? ????????? — ?? ??????? ????????? ?? ??????????? ?????? ? ?????????????. ?????????? ?? ????? ? ???????? ?????? ????? ????? https://yuridicheskaya-kompaniya-krasnodar.ru/ ? ??????? ????? ?? ????????. ????? ??????? ??????? ?????????? ???????? ????????????????? ????????? ? ?????? ????? ????????? ? ????? ???? ?????????.
I need to explain something the majority of septic companies won’t: there are two kinds of people in this world. Those who believe septic systems are just “underground boxes for waste,” and those who have had raw sewage erupting into their yard at 2 AM. I learned this difference the hard way in 2005—waist-deep in sludge, trembling in a Washington downpour, as my family and I helped a weathered installer fix our family’s collapsed system. I was 14. My hands ached. My clothes were destroyed. But that evening, something crystallized: This isn’t just manual labor. It’s people’s lives that we’re protecting.
Here’s the dirty truth: nearly all septic companies just pump tanks. They act like band-aid salesmen at a disaster convention. But Septic Solutions? They are different. It all originated back in the early 2000s when Art and his siblings—just kids scarcely tall enough to lift a shovel—assisted install their family’s septic system alongside a grizzled pro. Imagine this: three pre-teens buried in Pennsylvania clay, understanding how soil absorption affects drainage while their friends played Xbox. “We didn’t just dig trenches,” Art shared with me last winter, hot coffee cup in hand. “We understood how ground whispers mysteries. A patch of wetland vegetation here? That’s Mother Nature yelling ‘high water table.'”
https://hive.blog/hive-178708/@praditya/the-progress
???????_???????_?_????????? ???????????: ?????? ?????? ?????
This is the ugly truth: the majority of HVAC failures occur because someone skipped a step. Did not calculate the load accurately. Used incorrect equipment. Got wrong the insulation needs. We’ve fixed dozens of these failures. And each time, we record another insight. Like in 2017, when we began adding WiFi controls to each install. Why? Because Sarah, our lead tech, got frustrated of watching homeowners waste money on inefficient temperature control. Now clients save $500+ yearly.
https://us.enrollbusiness.com/BusinessProfile/7668666/Product%20Air%20Heating,%20Cooling,%20and%20Electric
????? ????? ? ?????? ??????? ???????? ???????? ?? ????? ????? https://hoteltukan.ru/ – ??? ??????? ????????????, ?????????? ??????, ???????? ? ???????. ?????????? ?? ????? ???? ?????? – ??? ??? ??????????! ? ????? ?????? ????????????? ???? ?? ??? ?? ??????. ????????? ???????? ? ??????????? ????? ? ???, ??? ???? ? ????????? ??????????? ??? ????? ????????????? ? ?????????????? ????????.
Let me share the brutal truth: nearly all HVAC failures happen because someone skipped a step. Did not calculate the load properly. Used incorrect equipment. Misjudged the insulation needs. We’ve personally fixed countless of these disasters. And every time, we remember another lesson. Like in 2017, when we decided on adding smart thermostats to every installation. Why? Because Sarah, our master tech, got sick of watching homeowners lose money on inefficient temperature control. Now clients save $500+ yearly.
https://www.crunchbase.com/organization/product-air-heating-cooling-and-electric
??????? ??????? ab-resurs.ru ?????????????? ??????? ??? ???????? ??????????? ? ??????????. ???????? ??????? ??? ?????????? ?????? ????????? ???????: ??????? ????? ???, ???????????????? ?????? ?? ??????????, ???????????? ????????????, ???????? ? ??????????? ???????? ??? ??????? ? ??????????? ?? ???? ??????
????????
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
Global Alternative Trade Financing Global Alternative Trade Financing: Looking ahead, Global Alternative Trade Financing is poised to play an increasingly significant role in shaping the future of global trade. As technology continues to evolve and new financial innovations emerge, we can expect to see even more sophisticated and accessible solutions that empower businesses to overcome financial barriers and participate fully in the global economy. This will require collaboration between governments, regulators, financial institutions, and technology providers to create a supportive ecosystem that fosters innovation, mitigates risk, and promotes sustainable and inclusive economic growth.
???? ?? ???? ???? ????? ? ????? ????? ????? ????????? ??????.
???????? ???????, ?? ????? ?????????? ??????????.
? ??????????? ???????? ???????????? ???????? ???????? eldorado casino ??????????? ????? ????????, ???????? ??????? ? ????????? ?????????.
??????? ?????? ??? ????? ? ????????? ???? ?????? ??????????? ???… stajler-dsn.ru .
??????? ??????? faamru.com ?????????????? ??????? ??? ???????? ???????????, ?????????, ?????????????? ? ??????????. ??????? ??? ??????????? ????????? ??????: ?????????? ????????, ?????? ??????, ???????? ?????? ? ??????? ??????, ?????? ? ???????? ??? ?? ?????????? ??????? ? ??????????? ???????? ??? ??????
?????? ??? ?????? ??????????? dn-fen-kupit.ru .
??? ?????? ?????? ? ?????? fen-dn-kupit-12.ru .
??????? ?????? ??? ????? ?????? ??????????? ???? ? ????????? ???… ??????? ?????? ??? ????? ?????? ??????????? ???? ? ????????? ???… .
???????????? ???????? “???????? ?????????” ????? ???? ??? ???????????? ???????????? ? ?????????? ????????? ?????????? ?? ?????? ? ????. ????? ???????????????? ?? ?????? ?????????, ?????????????? ? ????????? ? ????????????????? ?????????? ??? ????????????? ????????, ????????????? ????? ? ??????????? ????????? ????????. ?????? ???????? ????????? ????????? ????? ? ???????? ????????? ? ??????????? ???? ???? ????????????. ?? ???????? https://krasnodar-transport.ru/ ???????????? ?????? ? ????????? ?????????? ?? ??????? ????????. ????????????? ?????? ??????????, ?????? ?????? ? ??????? ???? – ??????? ????????????, ?? ??????? ??????? ???????? ??? ????????.
??????????? ???? ?????? ??????? ??? ????? ?????? ???? ? ????????… ??????????? ???? ?????? ??????? ??? ????? ?????? ???? ? ????????… .
??? ?????? ??? ???????? ???????? dn-fen-kupit-1.ru .
??????? ?????? ?????? ? ?????? pylesos-dn.ru .
????? ??????? ?????? ??? ????????, ???????, ?????????? ???????? https://victoryhome.ru/ – ??? ?????? ????, ? ??? ??? ? ???????, ????, ???????, ?????, ?????, ?????????, ??????????, ????, ???????? ? ?????? ??????. ?????? ? ????? ?????????? ?????????, ??? ???????? ??? ???????? ?????????? ?????????? ?????? ????. ????????? ?? ?????.
https://t.me/s/minimalnii_deposit/74
Here’s the harsh truth: the majority of HVAC failures occur because someone skipped a step. Didn’t calculate the load accurately. Used undersized equipment. Misjudged the insulation needs. We’ve personally fixed dozens of these failures. And each time, we record another lesson. Like in 2017, when we started adding remote monitoring to all install. Why? Because Sarah, our master tech, got tired of watching homeowners burn money on inefficient temperature control. Now clients save hundreds yearly.
https://productairheating.mystrikingly.com/
This content is well-organized and easy to understand. It really helped me a lot.
?????-????? ? ????????? ? ??? Gentalion https://gentalion.ru/ ? ????? ??????????? ? ?????? ?????? – ??? ???????? ? ?????????? ??????, ???????????? ?????? ? ??????????? ?????????????? ?????????! ??? ????? ?????? ? ?????????? ????????????? ???????: ?????? ??????, ???????? ??????, ????????????? ???????. ???????, ?????????? ? ?????? ? ???????? ??????? ??? ? ??? ? ??????!
Allow me to explain something most septic companies won’t: there are two categories of people in this life. Those who think septic systems are simply “underground boxes for waste,” and those who’ve had raw sewage erupting into their yard at 2 AM. I understood this distinction the difficult way in 2005—waist-deep in sludge, trembling in a Washington deluge, as my siblings and I aided a veteran installer repair our family’s broken system. I was fourteen. My hands were raw. My pants were ruined. But that night, something changed: This is not just manual labor. It’s families’ lives that we’re safeguarding.
Let me share the dirty truth: most septic companies just pump tanks. They are like quick-fix salesmen at a disaster convention. But Septic Solutions? They are different. It all originated back in the early 2000s when Art and his brothers—just kids barely tall enough to shoulder a shovel—assisted install their family’s septic system alongside a weathered pro. Imagine this: three kids waist-deep in Pennsylvania clay, discovering how soil permeability affects drainage while their friends played Xbox. “We never just dig trenches,” Art shared with me last winter, warm coffee cup in hand. “We understood how earth whispers secrets. A patch of marsh plants here? That’s Mother Nature shouting ‘high water table.'”
https://www.keepandshare.com/discuss2/39026/random-backflow-during-heavy-showers
??????????? ???? ?????? ??????? ?????? stajler-dsn.ru .
??????????? ???????? ???? ????? https://nashabelka.ru/ ????????? ?????? ?? ?????? ???? ????? ????????? – ?? ??????????? ?????? ?? ????? ???? ? ??????. ??????? ??? ???? ????? ???????? ???????????? ?? ????? ? ????? ????? ??????? ?? ?????????? ? ??????????????? ?????????. ????????????? ???? ????????? ? ??????? ?? ???????? ?????!
??????? ?????? ??? ????? ???? ? ????????? ??????????? ???? ?????… ??????? ?????? ??? ????? ???? ? ????????? ??????????? ???? ?????… .
?????????? DreamStalker Expert ?????? ????????? ???????? ??????????????????? ??????, ?????????? ???????????? ???????????, ????? ???????? ???????????? ???????? ???? ? ????????????? ????????????. ????? ??????? ????????????? ???????? DreamStalker? ?laps.me/catalog/pribory-dlya-osoznannykh-snov/pribor-dlya-osoznannykh-snovideniy-dreamstalker-expert/ ?????????? ?????????? ? ??????????? ????????? ?????-?????? ? ???????????????? ?????????? tACS, ?????????????? ??????? ?????????? ? ?????????? ???????????. ?????? ??????????? ? ??????? ????????? ? ???????????? ??????? ???????? ?? ?????????????? ???????.
?? ????? ??????? ?????? ?????????? – ??? ??? ???? ???????????????? ?????????, ????????? ?????????????????? ? ?????? ???????? ? ???????????. ?????? ?????????? ? ???????? ????? ???????? ? ???? ????????? ???????, ???????????????? ???????? ? ??????? ????????? ???????? ?? ???????? ??? ??????.
??? ?????? ?????? ? ?????? fen-dn-kupit-13.ru .
??????????? ?????? fen-dn-kupit-12.ru .
Omnigram https://omnigram.ru/ — CRM ? ?????????: ???????? ??????? ?? WhatsApp, Avito, Telegram-?????, Gmail ? ?????? ??????? ????? ? Telegram-?????? ? ???????? ?? ????????. ??????? ???????? ??????, ?????? ?????????? ???????, ?????? ??????? ?????? ????????? (/paid, /closed), ?????????? ??-????????? ? ???????/API. ????? — ?? ???? ????? (QR). ????? ?? 1000 ?/???: 5 000 ????????? ? 1 ???; ?????? — pay-as-you-go. ???????? ?? ????? ??????????, ?????? ????? ????????????.
?????? ?????? ??????? ? ????????? ??????????? ???? ??? ????? ???… stajler-dsn-1.ru .
This is the harsh truth: the majority of HVAC failures happen because someone missed a step. Didn’t calculate the load properly. Used incorrect equipment. Misjudged the insulation needs. We’ve fixed countless of these disasters. And every time, we file away another insight. Like in 2017, when we started adding WiFi controls to each system. Why? Because Sarah, our senior tech, got tired of watching homeowners burn money on inefficient temperature management. Now clients save 20-30% yearly.
https://vocal.media/authors/product-air-heating-cooling-and-electric
Hello, I desire to subscribe for this blog to get most recent updates, therefore where can i do it please assist.
Dragon Money Casino
??? ?????? ?????? ? ?????? dn-fen-kupit-1.ru .
?????? ??????? ?????? ? ?????? ???????? pylesos-dn-2.ru .
??????? ?????? ??? ?????? pylesos-dn.ru .
??? ?????? ?????? ??????????? stajler-dsn.ru .
?????? ??????? ??? ????? ??????????? ???? ? ????????? ?????? ???… ?????? ??????? ??? ????? ??????????? ???? ? ????????? ?????? ???… .
???????? ?????? 2025 ?????????? ???? ???????? ???????????
dyson ??? ?????? ???????? dyson ??? ?????? ???????? .
?????? ??????? ?????? ??????????? ???? ???? ??? ????? ? ????????… ?????? ??????? ?????? ??????????? ???? ???? ??? ????? ? ????????… .
?????? ??? ?????? ???????? ? ?????? ??????????? ???? ?????? ??? ?????? ???????? ? ?????? ??????????? ???? .
This is the harsh truth: nearly all HVAC failures take place because someone skipped a step. Did not calculate the load properly. Used incorrect equipment. Misjudged the insulation needs. We’ve fixed countless of these messes. And every time, we record another lesson. Like in 2017, when we started adding remote monitoring to each system. Why? Because Sarah, our lead tech, got tired of watching homeowners lose money on bad temperature settings. Now clients save $500+ yearly.
https://www.band.us/band/100887546/intro
??????? ?????? ?????? ?? ????????? pylesos-dn-2.ru .
????? ????? ???????? ????? ????? ???????? ? ???? ????????? ???????????, ?? ????????????? ??????? ? ??????? ?? ?????? ? ???????? ??????? ? ????????. ?????? ??????? ??????? ?????????? ?????????? ???? ? ??????, ? ????? ?????? ???????? ? ???????? ??????? ????????. ???????? ?????? ??????? ?? ??? ?????, ???????????? ? ????? ??????.
?????? ??????? ??? ????? ? ????????? ???? ?????? ??????????? ???… stajler-dsn.ru .
?????? ??????? ?????? ??????????? ???? ???? ??? ????? ? ????????… ?????? ??????? ?????? ??????????? ???? ???? ??? ????? ? ????????… .
I need to explain something most septic companies won’t: there are two kinds of people in this life. Those who assume septic systems are just “underground boxes for waste,” and those who have had raw sewage gurgling into their backyard at midnight. I discovered this distinction the hard way in 2005—standing in sludge, trembling in a Washington rainstorm, as my siblings and I helped a weathered installer restore our family’s collapsed system. I was fourteen. My hands blistered. My jeans were ruined. But that moment, something crystallized: This is not just dirt work. It’s people’s lives that we’re protecting.
Let me share the ugly truth: the majority of septic companies just pump tanks. They are like quick-fix salesmen at a chainsaw convention. But Septic Solutions? They are special. It all began back in the beginning of the 2000s when Art and his siblings—just kids hardly tall enough to shoulder a shovel—assisted install their family’s septic system alongside a experienced pro. Imagine this: three youngsters buried in Pennsylvania clay, understanding how soil absorption affects drainage while their buddies played Xbox. “We never just dig holes,” Art shared with me last winter, hot coffee cup in hand. “We understood how soil whispers secrets. A patch of wetland vegetation here? That’s Mother Nature screaming ‘high water table.'”
https://steemit.com/learn/@sarnalisa/drawing-study-for-septic-tank
???????????? ???? ??????? ????????????????? ??????? ? ??????????????, ?????????? ? ???????????? ???????????? ????????. ???????? ????? ???????????????? ?? ???????? ????????????? ???????? ??? ???????, ???????????????? ????? ? ????????????? ??????????. ?????????? ???????? ???? ??????????? ??????????? ???????? ? ????????? ???????????????? ?????????????? ?????? ????. ??????????? ????????? ?????? ? ????????? ?? ???? ???, ????????? ????????????????? ????????? ???????????? ????????. ????????? ?? ??????? ? ??????????? ????? ?????? ?? ????? https://mvpol.ru/ ? ??????? ????????. ?????????? ????? ???????? ? ??????????? ????? ???????? ????? ???????????? ?????? ?????????????.
Pickups ????????????? ?????? RAM ????????? ???????????? ????????? ??????????, ???????? ? ???????????? ????????????. ????? ramforum.ru ?????????? ?????????? ???? ??????????? ?????????? ? ?????? ??? ?????? ??????, ?????????? ??????????? ???????????? ? ??????? ???????????? ???????? ????????????. ????? ????? ????? ????????? ?????? ??????? RAM 1500 ? ????????????? Limited, Rebel ? Tungsten, ?????? ? ????????? ?????????? ? ?????????? ???????????. ?? ?????? http://ramforum.ru/ ???????? ????????? ??????? ???????????? ????? ???????????, ???????? ?? ?????? ??????????????? ???????????? ? ?????????????? ?? ????????????. ??????????????? ? ?????????? ???????????, ????? ???????? ????????????? ?????????? ?? ??????????? RAM ?? ???????? ??????????.
?????????_????_??????? ?????????????????: ?????? ??????? ??????????
?????? ??????? ?????? ??????????? ???? ?????? ??????? ?????? ??????????? ???? .
??????? ?????? 2025 ?????? pylesos-dn.ru .
?????? ??????? ??? ????? ? ????????? ???? ??????????? ???? ?????… ?????? ??????? ??? ????? ? ????????? ???? ??????????? ???? ?????… .
?????? ??????? ??? ????? ???? ? ????????? ?????? ??????????? ???… fen-dn-kupit-12.ru .
Here’s the ugly truth: the majority of HVAC failures happen because someone missed a step. Did not calculate the load correctly. Used incorrect equipment. Miscalculated the insulation needs. We’ve personally fixed hundreds of these messes. And each and every time, we record another learning. Like in 2017, when we decided on adding remote monitoring to each installation. Why? Because Sarah, our senior tech, got frustrated of watching homeowners burn money on inefficient temperature settings. Now clients save $500+ yearly.
https://about.me/productairheating
?????? ?????? ? ?????? ???????? stajler-dsn-1.ru .
??????? dyson absolute ??????? dyson absolute .
???????? ?????? ?????? 2025 ???????? ?????? ??? ?????????? ?? ???
Davin Chiri Zorve19 ??????????????????????????????????????????????????? https://motionworks.jp/ ???????????????????????????????????
dyson v12 ??????? dyson v12 ??????? .
???????? ??????????????? ? ??????????? ???????????? ??????? ????????????????? ??????? ? ???????????? ??????????. ???????? Glassway ???????????????? ?? ???????????? ????????? ????????, ??????????? ???????????, ?????? ? ???????????? ???????????? ??? ??????, ???????? ??????? ? ???????????? ????????. ??????????? ???????????? ????????? ?????????? ????????? ?? ????????? ????? ? ????????? ???????? ? ??????? ????????? ??????????????. ???????? https://glassway.group/ ????? ???????????? ? ?????? ????????? ???????: ?? ????????? ???????? ? ?????????? ??????????? ?? ?????-?????? ? ???????????? ???????. ???????????????? ??????? ???????? ????????? ?????? ????? ?????????, ???????? ? ????? ????? ?????? ???????????? ??????? ??? ?????? ???????.
????? ? ?????????? ??????? ??????? ??????? — ????? ????? ?????, ??? ????? ???????????? ????? ?? ????. ????? ? ??????? ?? ??????? ????????????? ????? ?????????? ?????? ????????? ????? ???????????? ??????? ? ???????? ?????????????. ????? ???????? ?????? ? ?????? ?? ??????, ???????? ?????? ?????????? ?????? ? ??????? ??? ??????? ???????. ????????? ??????? ????????? ? ?????????? ??????????? — ????????? ????????? ??????????? ??????? ? ????????. ????????? ?? ??????? ? ?????????? ????? ????? ?????? ?? https://sauna-koptevo.ru/ ????? ????????????? ???????. ????????? ??????? ? ?????????? ?????????? ???? ??????????? ?????????? ????? ??? ???????? ?? ????? ???????.
???????? «???????????» ?? ???????? ???????????? ??????????? ???????????? ?????-???? ? ???????????? ??????? ?? ???????? ??? ?????????? ? ??????????? ??????????. ????? ? 10-?????? ????????? ????????? ?????? ????????? ?????????: ?? ?????????? 3D-??????? ?? ?????? ????????? ???????. ????????? ? ???????????? ? ?????? ???????? ????? ?????? ?? https://press-forma.by/ – ????? ???????????? ??????? ?????, ??????? ??????? ???? ? ??????? ??????????????. ??????? ???????? ???????? ?????????? ??????, ????????????? ??????????? ??????? ? ?????? ? 2-3 ???? ???? ?? ????????? ? ????????? ?????????????.
???????????? ???????? ?????? ?????? ? ?????? ???????????? ???????? ?????? ?????? ? ?????? .
???????? ?????? v11 ?????? pylesos-dn-2.ru .
?????? ??????? ??? ????? ??????????? ???? ???? ?????? ? ????????… ?????? ??????? ??? ????? ??????????? ???? ???? ?????? ? ????????… .
Let me share the harsh truth: nearly all HVAC failures take place because someone ignored a step. Did not calculate the load accurately. Used cheap equipment. Got wrong the insulation needs. We’ve fixed dozens of these failures. And every time, we record another insight. Like in 2017, when we started adding smart thermostats to every system. Why? Because Sarah, our senior tech, got frustrated of watching homeowners waste money on poor temperature control. Now clients save $500+ yearly.
https://www.brownbook.net/business/54577473/product-air-heating
?????? ??????? ?????? ? ???????????? pylesos-dn.ru .
??????????? ???????? ? ?????????????? ??????????????? ???????? ?????????? ????? ??? ??????????? ? ????? AREON. ?????? ?????? ?????? ????????? ?????????????? ??????????? ????? ?????????? ??????? ? ???????? ???. ?????????? ??????? ????? ?????????? ??????.??? ???????????? ?????????? ??????????????? ? ??????????? ?????? ? ?????????. ??? ??????????? ??????????? ???????, ???????????? ????? ????????? B ? ?????????? ?? ???????????? ?????. ????? ????????? ?????????? ? ??????? ? ???????? ????????? ?? https://parkareon.ru/ ??? ???? ????????. ?????????? ?????? ???????+ ? ?????? ???????? ????? ??????????? ???????????? ???????? ? ?????????????.
??????? ?????? ?????? ? ?????????? pylesos-dsn-1.ru .
Here’s the harsh truth: most HVAC failures occur because someone ignored a step. Did not calculate the load properly. Used cheap equipment. Miscalculated the insulation needs. We have fixed countless of these disasters. And each time, we remember another lesson. Like in 2017, when we started adding WiFi controls to every installation. Why? Because Sarah, our senior tech, got frustrated of watching homeowners burn money on inefficient temperature settings. Now clients save hundreds yearly.
https://www.producthunt.com/@productairheating
Let me explain something the majority of septic companies refuse to: there are two kinds of people in this reality. Those who believe septic systems are merely “subterranean tanks for waste,” and those who have had raw sewage erupting into their property at midnight. I learned this reality the hard way in 2005—waist-deep in muck, shivering in a Washington rainstorm, as my family and I helped a veteran installer fix our family’s broken system. I was fourteen. My hands were raw. My clothes were wrecked. But that evening, something clicked: This isn’t just dirt work. It’s folks’ lives we are protecting.
Let me share the dirty truth: the majority of septic companies just pump tanks. They’re like quick-fix salesmen at a chainsaw convention. But Septic Solutions? They are unique. It all originated back in the early 2000s when Art and his brothers—just kids scarcely tall enough to carry a shovel—aided install their family’s septic system alongside a weathered pro. Picture this: three kids buried in Pennsylvania clay, discovering how soil absorption affects drainage while their buddies played Xbox. “We never just dig holes,” Art shared with me last winter, warm coffee cup in hand. “We learned how earth whispers mysteries. A patch of wetland vegetation here? That’s Mother Nature screaming ‘high water table.'”
https://steemit.com/learn/@sarnalisa/drawing-study-for-septic-tank
????? ????????????? ?????????? ???? ??? ???? ? ?????????? ? ????????????? ????? ???????? ???? https://masterim-novostroy.ru/ – ?????????? ???? ??????? ? ??????? ??????? ?????? ??? ?? 2 ??????! ? ??? ????????????? ?? ????????? ????? ?? ???? ??? ????? — ?? ???????? ??????? ? ???????????? ?? ???????? ??????? ? ??????. ??????? ????????? ?? ????? ? ???????? ????? ????????? ? ?????? ????????????!
?????? ??????? ?????? ? ?????????? ?????? ??????? ?????? ? ?????????? .
?????? ??? ?????? ??????? ???????????? ?????????? ????????????, ?????? ? ????????? ??? Roblox — ? ?? ??????? ????? ????????? ????????, ???????? ????? ??????? ? ????????????? ????. ?? ????? ??????? ??????? https://joyverse.ru/ ????????? ??????????? ?????? ???????, ???? ? ?????? ?? ???? ???????, ??????? ????? ??????????? ??? ????????, ??? ? ??????? ???????.
??????????? ??????? ??????? ????????????????? ??????? — ?????? ? ?????????? ??? ?????????? ????? ?????? ??????? ? ?????. ??????? ??????? ???????????? ? ?????????? ?????????? ?????????? ????????? ???????????? ?? ????????, ???????? ? ????????????? ??????. ???????? ???????? ????????? ?????? ???????? ? ????????????? ?????? ???????? ?????????? ???????? ??? ???????. ???????? ???????? ? ?????? ????? ????????? — ?? ??????? ????????? ?? ??????????? ?????? ? ?????????????. ?????????? ?? ????? ? ???????? ?????? ????? ????? https://yuridicheskaya-kompaniya-krasnodar.ru/ ? ??????? ????? ?? ????????. ????? ??????? ??????? ?????????? ???????? ????????????????? ????????? ? ?????? ????? ????????? ? ????? ???? ?????????.
????? ??? ?????????? ?????????? DreamStalker Expert ?????????? ????????? ?? ??????????? ????????????? ???????? Wi-Fi ???????????, ????? ????????? ???????? ????, RGB-???????????? ? OLED-????????. ?????????? ???????? ?? https://claps.me/catalog/pribory-dlya-osoznannykh-snov/pribor-dlya-osoznannykh-snovideniy-dreamstalker-expert/ ? ??????? ????????? ? ????????? ?????-?????? ? ???????????????? ?????????? tACS. ??????? ???????????? ?????????? ????, ???????? ???????????? ? ????? ???????????? ???????????? ?????????? ???????????.
Here’s the harsh truth: the majority of HVAC failures take place because someone skipped a step. Didn’t calculate the load properly. Used undersized equipment. Misjudged the insulation needs. We have fixed hundreds of these messes. And each time, we record another insight. Like in 2017, when we began adding remote monitoring to every system. Why? Because Sarah, our senior tech, got sick of watching homeowners waste money on bad temperature control. Now clients save 20-30% yearly.
https://www.tumblr.com/productairheating2/802845984814153728/product-air-heating-cooling-and-electric?source=share
Allow me to share with you something the majority of septic companies refuse to: there are two categories of people in this reality. Those who assume septic systems are merely “underground boxes for waste,” and those that have had raw sewage bubbling into their yard at midnight. I learned this distinction the hard way in 2005—standing in sludge, shivering in a Washington deluge, as my siblings and I helped a weathered installer repair our family’s failed system. I was a teenager. My hands blistered. My jeans were wrecked. But that night, something changed: This isn’t just dirt work. It’s families’ lives that we’re safeguarding.
Here’s the harsh truth: nearly all septic companies just maintain tanks. They’re like quick-fix salesmen at a demolition convention. But Septic Solutions? These guys are special. It all originated back in the beginning of the 2000s when Art and his family—just kids scarcely tall enough to shoulder a shovel—aided install their family’s septic system alongside a weathered pro. Visualize this: three pre-teens waist-deep in Pennsylvania clay, understanding how soil permeability affects drainage while their buddies played Xbox. “We didn’t just dig trenches,” Art told me last winter, hot coffee cup in hand. “We learned how earth whispers mysteries. A patch of marsh plants here? That’s Mother Nature yelling ‘high water table.'”
https://hive.blog/hive-178708/@praditya/the-progress
????????????-???????????? ??? ?????????????? ?????? ???????? ????????? ??????? ??? ?????????, ?? ????????????? ????????? ???? ????????? ????? ???????. ??????????? ???????????? ????? ??????????? ??????????????? ????????, ??????? ????????? ????????? ??????? ???????? ? ???????? ???? ?????????? ??????. ??????????? ???????????? ???????? ?????????? ????? ???????????? ?? 4,8 ?????? ? ???????? ????? ?????? ?? 37%. ????????? ?????????? ? ????????? ????????, ?????????? ? ?????????? ????? ????? ?? https://indenza.com.ru/ — ?????????????????? ??????? ??? ????????? ? ??????. ???????? ?????? — ????? ???? ??? ? ???? ??????????? ???? 160 ?? — ?????? ??????? ??????????, ? ???????????? ??????????? ???????? ?????????????? ??? ???????.
??????? ?????? ?????? ??????????? ???? dn-fen-kupit.ru .
?????? ??????? ??? ????? ? ????????? ??????????? ???? ???? ?????… ?????? ??????? ??? ????? ? ????????? ??????????? ???? ???? ?????… .
??? ?????? dyson ??? ?????? dyson .
???????? ??? ???? ?????? ?????? pylesos-dsn-1.ru .
?????? ?????? ??????? ??? ????? ? ????????? ??????????? ???? ???… fen-dn-kupit-12.ru .
Let me share the ugly truth: nearly all HVAC failures take place because someone missed a step. Didn’t calculate the load properly. Used cheap equipment. Miscalculated the insulation needs. We’ve fixed countless of these disasters. And each and every time, we file away another learning. Like in 2017, when we decided on adding WiFi controls to each system. Why? Because Sarah, our senior tech, got frustrated of watching homeowners lose money on inefficient temperature management. Now clients save 20-30% yearly.
https://www.b2bco.com/productairheating
?????? NVMe VPS/VDS https://xhost24.com ?????? ??????????? ??????? ? ???????? SSD NVMe. ??????? ??????????????????, ?????????? ????, ?????? ? ??????? ??????????. ???????? ??? e-commerce, API, CRM, ??????? ? ???-???????? ?????? ????????.
jailbailt & teen
? ???????? ????????? ???? ??? ??????? ??????, ?????????? ??????? ??????. ??? ??????? ?? ???????? ???? — ??? ?????????? ??????, ????? ? ??????? ??????? ???????, ??? ??????????? ????????? ? ?? ?????. ????? ????? ??????????, ???????? ??????? ???????? ? ???????????, ??????? ??????? ?? ?????? ????. ?????? ??????: ???? ??????? ???????, ???? ???????? ??????????. ??????? ??????? ????? ??????? ????? ?????? ? ???????, ??? ?? ?????? ????????? ????? ??????.
????? ??????? ?????? ????? ?????? stajler-dsn-1.ru .
??????? dyson v15 ?????? ??????? dyson v15 ?????? .
?????? ?????? ??????????? ???? ?? ??????? ? ??????? ?????? 1080p
??????? ?????? ?????? ? ?????? ??????? ?????? ?????? ? ?????? .
????? ??????????? ?????? ?????? vypryamitel-dn.ru .
??? ??????????? ?????? airstrait vypryamitel-dn-1.ru .
??????? ?????? ???????????? ???????????? ?????? ? ?????? dn-pylesos.ru .
??????????? dyson ?????? ??????????? dyson ?????? .
dyson v12 ??????? dyson v12 ??????? .
Here’s the harsh truth: the majority of HVAC failures happen because someone missed a step. Failed to calculate the load correctly. Used cheap equipment. Misjudged the insulation needs. We have fixed dozens of these messes. And each and every time, we file away another lesson. Like in 2017, when we began adding WiFi controls to each install. Why? Because Sarah, our senior tech, got tired of watching homeowners lose money on bad temperature control. Now clients save 20-30% yearly.
https://www.brownbook.net/business/54577473/product-air-heating
????? ? FC Mobile Rise of Kingdoms – ?????????? ????????? ?????????, ??? ????? ?????? ???????????? ???? ? ????????? ???????? ???????????. ????? ????????? ????????? ????????? ????????????? ??????, ???????? ????? ? ???????????? ??????????, ??? ???? ??????? ???????????? ? ????? ?? ?????????????. VIP-??????, ????????????? ?? ?????, ????????????? ?????????????? ?????? ? ??????????. ??????, ????? ???????, ??? Rise of Kingdoms – ??? ? ?????? ??????? ?????????????? ????, ? ?????? ???????, ?????????? ? ?????????????? ? ???????? ?????? ?? ????? ?????? ????, ??? ?????????? ????????.
???????? ??????? ???????? ????????? ?????? ???? ? ???? ?????? ????? ??????????, ????????? ????????? ???????, ??? ????????? ????????? ???????? ??????? ? ???????? ???????????, ??????? ?????? ??? ????? ?????????, ??? ?????? ??????? ???????, ?????? ??????? ???????, ? ?????? ????? ??????? ????? ??????? – ??????? ????????? ??????? ?????? ? ??????
Mobil telefondan pinco oyna seçimi m?nim üçün ?n böyük üstünlükdür. Bu platforma haqq?nda ?trafl? m?lumat? burada tapmaq olar: pinco. Mobil t?tbiq axtaranlar pinco casino app download variant?na baxa bil?r. Pinco casino azerbaycan bonus ??rtl?ri ayd?n göst?rilir.
Pinko giris prosesi sad? v? sür?tlidir. Pinco az telegram üz?rind?n ?laq? saxlamaq mümkündür. Pinco casino oyunlar? stabil server üz?rind? i?l?yir. Canl? futbol m?rcl?ri pinco sports üz?rind?n mümkündür. Pinco haqq?nda ??rhl?r platforman? seçm?y? köm?k edir. Pinco az sayt?nda qaydalar asan ba?a dü?ülür.
Pinco az?rbaycan sayt?nda qeydiyyat prosesi çox sür?tlidir. Birba?a r?smi s?hif? buradad?r: https://domen.com. Pinco az yukle ed?r?k mobil m?rcl?r? ba?lamaq mümkündür. Pinco bonus t?klifl?ri yeni istifad?çil?r üçün maraql?d?r.
Hesaba giri? pinco casino login vasit?sil? problemsizdir. Pinco az tg vasit?sil? bonuslar elan edilir. Pinco kazino oyunlar? mobil cihazlarda da rahat aç?l?r. Pinco sports m?rcl?ri real vaxtda yenil?nir. Pinco casino bar?d? oxuduqlar?m gerç?k oldu. Pinco kazino interfeysi sad? dizayna malikdir.
????? ??? ?????? ??????????? ??? ????? ?????? vypryamitel-dn.ru .
?????? ??????????? ?????? ??????? vypryamitel-dn-3.ru .
??????? ?????? ???????????? ????????? ?????? ?????? dn-pylesos-kupit-1.ru .
I just could not depart your website prior to suggesting that I extremely enjoyed the standard information an individual supply in your guests? Is gonna be back continuously in order to inspect new posts
??? ??????????? ?????? ?????? ? ?? ??????????????? vypryamitel-dn-2.ru .
??????????? dyson corrale ??????????? dyson corrale .
???? ?????? ???????????? ????? ??????????? ?????
??????? ?????? ?????? ???????? ??????? ?????? ?????? ???????? .
Let me share the brutal truth: the majority of HVAC failures take place because someone missed a step. Didn’t calculate the load accurately. Used incorrect equipment. Miscalculated the insulation needs. We’ve personally fixed countless of these messes. And each and every time, we file away another insight. Like in 2017, when we began adding WiFi controls to every install. Why? Because Sarah, our lead tech, got frustrated of watching homeowners waste money on inefficient temperature control. Now clients save $500+ yearly.
https://groups.google.com/g/electric-motor-it-support/c/v-PiRO2Yugo
???????? ?????? ?? ????’??? ??????? 2026 ?????? ???????????
??????????? ?????? ?????? ? ??????? vypryamitel-dn-3.ru .
??????????? ?????? ?????? ? ????????????? vypryamitel-dn.ru .
????? ?????? ??????? ?????? dn-pylesos-kupit-1.ru .
business info hub – The site looks trustworthy and navigation is intuitive.
insights you can use – Offers ideas that feel immediately applicable and relevant.
?????? ??????????? ??? ????? ?????? ? ??? ?????? ??????????? ??? ????? ?????? ? ??? .
dyson ??????????? ???????? vypryamitel-dn-1.ru .
business knowledge click – Well-organized articles, help digest insights quickly and efficiently.
??????? ?????? v12 ?????? ??????? ?????? v12 ?????? .
Here’s the ugly truth: most HVAC failures take place because someone missed a step. Failed to calculate the load properly. Used undersized equipment. Misjudged the insulation needs. We’ve personally fixed hundreds of these disasters. And each and every time, we file away another learning. Like in 2017, when we decided on adding smart thermostats to all install. Why? Because Sarah, our lead tech, got tired of watching homeowners burn money on bad temperature settings. Now clients save $500+ yearly.
https://ezlocal.com/wa/marysville/air-compressor-repair-service/0919398403
insightful business tips – Excellent resources, made tricky topics much more approachable.
?????? ??????? ?????? ??????????? dn-pylesos.ru .
??????????? ?????? ???????? ??????????? ?????? ???????? .
applied insights portal – Content feels actionable and can be used immediately in practice.
insightful business updates – Platform shares clear insights, staying informed is easy and practical.
step-by-step growth – Practical advice, makes following through on projects simple and realistic.
?????? ??????? ?????? ????????? ?????? ??????? ?????? ????????? .
??????????? ?????? ?????? ? ??? vypryamitel-dn.ru .
fresh strategy ideas – The layout supports discovering concepts without distraction.
market alliance hub – Very insightful, helps understand alliances in real-world market situations.
release your energy – Strong and motivating, shows how letting energy flow sparks forward action.
?????? ??????????? ?????? ????? vypryamitel-dn-2.ru .
EasyDigitalShopping – User-friendly interface makes online purchases fast and convenient.
??????????? ?????? ? ??????????????? ???????? ????????? ??????? ????????????????? ??????? ? ?????????? ????????. ????????? “??????-???” ? ?????????? ???????????????? ?? ?????????? ?????????? ??? ???? ? ???????? ??????? ?????????? ?????. ? ???????? ???????? ????? ?????????? ????????: ?? ???????????? ??????????-??????? ?? ??????????? ?????? TikTok-????????? ? ?????????? ?????????? ????????????. ???????????????? ??????? ???????? ????????? ?????????? ?? ??? ????????, ????????? ? ??????? ???? ??? ?????????? ?????????. ?????? ?????? ? ?????????? ? ???????? ???????? ????? ?? ????? https://iriska-show.ru/ ??? ??????????? ?????? ??????? ????? ? ????????? ? ??????.
??? ??????????? ?????? ?????? ? ??????? vypryamitel-dn-1.ru .
LongTermOpportunitiesHub – Highly informative, the site makes spotting long-term prospects clear and simple.
??? ????? ?????? ???????? ??????? ???????? ???????? ???? ??????? ?????? ???? ???????? ??????? ?????? ????? ??????? ?????? ???????? ????????? ??? ????????? ??? ????? ??????? ????????? ??????? ???? ? ????? ?????? ???? ??? ?????? ????? ??? ????? ???????? ???? ?? ????? ??????? ? ????????? ??????: https://natyazhnye-potolki-moskva.ru/
safebuyhub – Makes online shopping simple, smooth, and secure.
???????? ??????? ???????? ? ??? ????????, ? ???????? ??????? ??????, ? ??? ?????, ? ??? ??????: ????????????? ??????????? ?? ?????? ????????? ? ???????? ??? ?????? ? ?????, ??????? ???????? ???????? ????????; ?????? ???????? ?? ???? ? ??? ????, https://potolki-decarat.ru/
partnership learning hub – Lessons are simple, partnership advice feels trustworthy.
Let me tell you something most septic companies will not: there are two types of people in this world. Those who think septic systems are merely “underground boxes for waste,” and those that have had raw sewage erupting into their yard at 2 AM. I discovered this reality the tough way in 2005—waist-deep in sludge, shivering in a Washington rainstorm, as my siblings and I helped a grizzled installer restore our family’s broken system. I was 14. My hands were raw. My pants were ruined. But that night, something changed: This ain’t just manual labor. It’s folks’ lives we’re protecting.
This is the dirty truth: most septic companies just maintain tanks. They’re like quick-fix salesmen at a chainsaw convention. But Septic Solutions? They are different. It all started back in the early 2000s when Art and his brothers—just kids barely tall enough to lift a shovel—assisted install their family’s septic system alongside a experienced pro. Imagine this: three kids waist-deep in Pennsylvania clay, learning how soil porosity affects drainage while their buddies played Xbox. “We never just dig holes,” Art told me last winter, warm coffee cup in hand. “We discovered how earth whispers mysteries. A patch of wetland vegetation here? That’s Mother Nature shouting ‘high water table.'”
https://www.fitday.com/fitness/forums/newcomers/42940-strange-odor-coming-basement-pipes.html
retaildigitalsolutions – Very practical and intuitive, shopping online feels quick and easy.
??????? dyson ?????? ? ??? ??????? dyson ?????? ? ??? .
goal flow planner – Well-explained strategies, supports taking actionable steps efficiently.
bizalliances – Clear and practical, connecting with professionals is structured and easy to follow.
???????? ??????? ???????? ???????? ???????????? ? ????????? ?????? ?????????, ???????? ?????????? ? ?? ??????????? ????????. ?? ????? ???????? ?????? ??????? ? ?????????? ??????????, ??? ???????? ?????? ??? ??????? ? ????? ???????? – https://potolki-decarat.ru/
trusted alliance resources – Informative content, helps relate alliances to practical business cases.
Here’s the ugly truth: nearly all HVAC failures happen because someone missed a step. Did not calculate the load accurately. Used cheap equipment. Miscalculated the insulation needs. We’ve personally fixed hundreds of these disasters. And each time, we record another insight. Like in 2017, when we began adding smart thermostats to each installation. Why? Because Sarah, our master tech, got frustrated of watching homeowners lose money on poor temperature control. Now clients save $500+ yearly.
https://homeguide.com/wa/everett/garage-door-repair/product-air-heating-xhvDmV4PL
forward with focus – Clear, actionable language highlighting intentional advancement.
BusinessUnityGuide – Structured content, enterprise framework concepts are easy to follow and understand.
BusinessTrustCenter – Trusted guidance, site is structured clearly for easy browsing.
corporategrowthpartners – Clear and practical, strategies for enterprise partnerships are actionable and well-organized.
learning made simple – Easy-to-follow tips that inspire consistent progress.
securepurchasehub – Online shopping made simple, trustworthy, and efficient.
Pinco il? onlayn casino v? idman m?rcl?ri bir yerd? çox rahat i?l?yir. Mobil istifad?çil?r üçün d? aç?qd?r: http://www.pinco-cazino.website.yandexcloud.net. Pinco azerbaycan yukle seçimi il? ist?nil?n yerd? oynamaq olur. Pinco casino azerbaycan bonus ??rtl?ri ayd?n göst?rilir.
Pinco giris s?hif?si mobil v? desktopda stabil aç?l?r. Pinco az?rbaycan tg kanal?nda yenilikl?r payla??l?r. Slot v? canl? oyunlar pinco gazino-da kifay?t q?d?rdir. Pinco sports bölm?si ayd?n strukturla?d?r?l?b. Pinco az?rbaycan oyunçular? üçün ?lveri?lidir. Pinco kazino interfeysi sad? dizayna malikdir.
InnovationInsightsHub – Fun and structured content, learning about new ideas is easy.
dyson ??????????? dsn-vypryamitel.ru .
??????????? ?????? airstrait ht01 ?????? ? ?????????? dsn-vypryamitel-1.ru .
???? ??????? ?? ????? http://www.aviator-plus.ru/ .
dyson ??? ??????????? ?????? dyson ??? ??????????? ?????? .
??????????? ?????? ?????? ? ??? ??????????? ?????? ?????? ? ??? .
??????????? dyson airstrait ht01 ???????? vypryamitel-dn-kupit.ru .
??? ?????? ???????? ??? ??????????? ?????? dsn-vypryamitel-4.ru .
build professional trust – Offers practical tips, forming connections feels simple.
??????????? ?????? ??? ?????? ???????? vypryamitel-dn-kupit-1.ru .
?????? ??????????? ? ????? ?????? ??????????? ? ????? .
smartgrowthinsights – Stepwise guidance that makes growth strategies easier to follow.
strategyinsider – Practical and informative, market strategies are easy to implement in real situations.
alliances knowledge base – Structured insights, helps make sense of market partnership dynamics.
clarity solutions – Informative and actionable, breaks down ideas clearly.
???? ??????? ?????? ????? ??????? ?????????? ??????? ? ??? ??????? ????? ???????? ??????? ?????? ???????? ????? ?? ??????? ???? ? ????? ??????? ?????? ???????? ??? ??????? ??????? ? ???????? ?? ?????? ????? ????? ?? ???????? ???????? ? ?????????? ??????? ???????? ????? ? ?????? ???? ???????, https://natyazhnye-potolki-moskva.ru/
InformedPathways – Step-by-step tips, helps navigate choices effectively and confidently.
action-powered strategy – Approachable phrasing demonstrating how dynamic steps strengthen plans.
enterpriseconnection – Simplifies managing partnerships that are strategic and results-driven.
Here’s the brutal truth: most HVAC failures occur because someone ignored a step. Didn’t calculate the load properly. Used incorrect equipment. Misjudged the insulation needs. We have fixed hundreds of these disasters. And each and every time, we file away another learning. Like in 2017, when we began adding remote monitoring to every installation. Why? Because Sarah, our master tech, got frustrated of watching homeowners burn money on bad temperature control. Now clients save 20-30% yearly.
https://www.producthunt.com/@productairheating
??????? ?????? ???? ?? ?2 https://montazh-ploskoj-kryshi.ru
?????? ??????? ????????????? https://ocenka-vliyaniya-stroitelstva.ru
???????? ???????????????? ?? ????????? ???????????? ??? ????????????? ???????????? ?????? ? ???????? ????? ?????????. ?? ????? https://profprud.ru/ ?? ??????? ??????? ????? ???????: ?? ????????? ?????????? ? ??????? ???? ?? ?????? ??????????, ????????? ????????????, ????????? ? ????????? ?????? ??? ????????. ?????????????? ? ??????????????? ?? ????????, ??? ? ?????? ????? ??????????? ??????????? ???????? ????????? ? ????????? ?? 10 ???.
corporate links center – Informative platform, connecting with businesses feels organized and easy.
learnfutureleaderskills – Very informative, future-focused skills are explained in a simple, actionable way.
DigitalBuyMaster – Convenient and modern, shopping online is easy to navigate.
buyingportal – Clear and practical, shopping online is fast and intuitive.
??????????? ?????? ?????? ? ?????? ??????????? ?????? ?????? ? ?????? .
??? ??????????? ?????? ???????? dsn-vypryamitel-2.ru .
??????????? dyson ?????? dsn-vypryamitel.ru .
hip shopping network – Items are relevant and the platform has a cool, urban feel.
??????????? ??? ????? dyson airstrait ?????? vypryamitel-dn-kupit.ru .
?????? ????????? ?????? ??????????? dsn-vypryamitel-3.ru .
??? ??????????? ?????? airstrait ?????? ??? ??????????? ?????? airstrait ?????? .
GrowthPathwayCenter – Clear, step-by-step strategies that simplify business expansion.
?????? ??? ??????????? ??? ????? ?????? ??? ??????????? ??? ????? .
Full Article Here: https://t.me/s/blog_puzzlefreegame/16
mindful productivity – Very clear guidance, makes staying focused and accomplishing tasks simpler.
???? ?? ?? ???????? ????????? ?????????? ?? ??????? ???? ?????????? ?????????? ??? ????????? ???????. ??????? ?????????????? ???????, ????????? ?????????? ? ?????????. ???????? ??? ????? ? ?/? ????. ???????????????? ?????????, ?????????? ????????? ? ?????????.
??????????? ??? ????? dyson airstrait ?????? vypryamitel-dn-kupit-2.ru .
signal-led path – Practical and approachable, showing how well-directed indicators maintain progress.
?????? ??????????? ?????? ????? ?????? ??????????? ?????? ????? .
optionnavigator – Simplifies decision-making and helps identify the most effective strategies.
LongTermStrategyCenter – Structured guidance, long-term business goals are explained clearly.
strategic alliance tips – Helpful guidance, connecting professionally is simple and effective.
????? ????? ??? ?????? ???? ?? ??????? ?? ?????????? ?????? ? ?????????? ???????? ??????, ??????? ???????? ?????? ??????????. ???? ?????? ???????????? ??????????? ???????? ?? ????? ???????, ? ? ???????????? ?? ??????? ????? ? ?????????? ?? ????? ????????????? ????. ??? ???? ?? ???????? ???, ??? ????????? ?????? ???? ?? ??????? — ??????? ?????? ???????? ??? ????????!
????? ????????? LEVEL DETAILING ?????????????????? ????????? ????? ?? ????? ? ?????????, ??? ????????? ? ??????????? ????????? ???????????, ????????? ???????? ?????? ???????? ????? ?? ????? ?? ????????????? ??????????. ??????? ?????? ? ????????? ????????? ? ?????? ??????: ??? ?? ?????? ????????? ??????? ?????? ????????? ???????????, ?? ? ???????? ?????????? ????????? ??????, ????????? ?????????? ???????????? ???.
purchaseportal – User-friendly and efficient, online shopping is seamless.
bestdealshop – Very intuitive, finding bargains is simple and checkout is safe.
???????? ????? ??????? ??????????? ????????????????? ?????, ???????? ????? ???? ???? ? ????? ? ????????? ? ?????????? ????????????. ??????? “?????? ????” ? ?????? ?????????? ???????????????? ?? ???????? ???????????? ? ???????????? ??????? ??? ???????? ??? ????????????? ???????? ?????????. ??????????? ???????????? ? ????????????????? ????? ???????????? ?????????? ?????????? ???????? ????? ?????????: ?? ???????????????? ??????? ??????? ??? ?? ??????????? ?????. ??????? ?????? ?? ????? https://kinder-dent.ru/ ??? ??????????? ?????? ?????? ????? ??? ????? ? ????????, ??????? ??????????, ???????????? ???????????? ? ?????????????? ??????????? ????? ?? ?????? ????? ?? ???? ?????. ?????????? ???????????? ???????????? ??????? ????????? ?????????????? ???? ???????.
trusted market network – Practical content, makes alliances easy to apply in actual markets.
SafeOnlinePurchase – Clear and dependable, checkout process feels quick and effortless.
???????? ??????? ???????? ????????, ??????? ? ?????????? ??? ??????? ?????, ???????? ?????? ???????? ??????? ??? ????????? ??????????, ? ????????????? ??????????? ???????????? ?????; ????????? ?????? ???????? ?? ???? ????, ??? ???? ? ?????? ??????? https://potolki-decarat.ru/
InspireValueOnline – Platform feels dynamic and helps generate new ideas effortlessly.
?????? ??????????? ????? ?????? ? ?????? dsn-vypryamitel-1.ru .
?????? ??????????? ?????? ???????? ?????? ??????????? ?????? ???????? .
direction guide – Very practical advice, makes planning steps toward goals clear and achievable.
enterprise bond guide – The pages communicate reliability and professionalism.
??????????? ?????? ?????? ? ?????? ???????? dsn-vypryamitel.ru .
relationshiphub – Explore strategies to strengthen professional ties effortlessly.
??? ??????????? ?????? ?????? ? ??????? vypryamitel-dn-kupit.ru .
This is the brutal truth: most HVAC failures take place because someone missed a step. Failed to calculate the load correctly. Used undersized equipment. Misjudged the insulation needs. We’ve fixed countless of these disasters. And each and every time, we record another lesson. Like in 2017, when we decided on adding smart thermostats to all installation. Why? Because Sarah, our senior tech, got tired of watching homeowners lose money on bad temperature control. Now clients save hundreds yearly.
https://500px.com/p/productairheating
??????? ?????????? ??????????? ?????????? ?????? ????????? ??????????? ???????? ??????: ? ??? ??????? ?? ??????? ???????? ??????????? ????????? ? ?????? ??? ??????? ? ??? ???? ?????????????? ???????? ??????. ?????????? ????????? ????? ? ???????? — ??????????? ???????? ?? ?????????. ??? ???? ?????? ??????? ????????, ? ????????? ?????????????? ???????? ??????????? ?????????? ? ??? ??????????.
Spot on with this write-up, I really feel this web site needs much more attention. I’ll probably be returning to see more, thanks for the info!
Do you want bonuses? CSGOFAST Bonus Code deposit bonuses, free cases, terms and conditions. A quick activation guide, FAQ, and the latest updates.
educate meaningfully – Really clear lessons, information is easy to follow.
??????????? ?????? ??????????? ?????? .
??????????? ?????? ??????????? ?????? .
onlineshoppinghub – Efficient and user-focused, navigating the site for purchases is hassle-free.
?????? ??? ??????????? ??? ????? ?????? ??? ??????????? ??? ????? .
??????????? dyson ???? ??????????? dyson ???? .
??????????????????????https://ropc.jp/ ?????????????????????????????????????????????????????????????????????????????????????????????????
growthconnections – Very practical, offers easy-to-follow steps for effective partnerships.
https://t.me/s/KAZINO_S_MINIMALNYM_DEPOZITOM
??????????? ?????? https://team-black-top.ru ??? ????: ?????, ?????????, ?????????, ??????????????, ??????? ? ??????. ???????? ??????? ? Google/??????, ??????????? ?????? ? ??????. ?????????? ??????????, ???????? KPI ? ?????? ?? ????????? — ?? ?????? ?? ??????????? ?????.
market alliance insights – Helpful tips, shows how alliances work in realistic settings.
partnership growth network – Engaging and professional, suitable for long-term business partnerships.
future growth center – Detailed insights that help users focus on steady progress over time.
HyperBuyOnline – Easy to find products, modern and sleek interface.
??????????? ?????? ?????? ??????????? ?????? ?????? .
Hi, I do believe this is a great site. I stumbledupon it 😉 I’m going to return yet again since i have book-marked it. Money and freedom is the best way to change, may you be rich and continue to guide other people.
LearningMasterPro – Structured and practical lessons, knowledge is easy to acquire and apply.
practicalapproach – Offers sensible advice that you can apply immediately in real situations.
Rebricek najlepsich kasin https://betrating.sk/casino-hry/automaty-online/miner-donkey-trouble/ na Slovensku: bezpecni prevadzkovatelia, lukrativne bonusy, hracie automaty a zive kasina, pohodlne platby a zakaznicka podpora. Cestne recenzie a aktualizovane zoznamy pre pohodlne online hranie.
TractionTips – Motivates forward movement with practical, actionable insights.
??? IT-?????? https://nashkomp.ru/ – ??? ????????? ? ???? ??????? ??????????. ????????? ????????? ?????????? ??????? ?? ????? ?????????, ?????? ??????? ?????? ? ????? ???????? ????????. ?? ????? ?? ??????? ????????? ????? ???????????? ???????????, ???????????? ??????????? ?? ???????????????? ? ?????? ?? ?????????????????. ?? ????? ?????? ? ???????: ?? ??????????? ?????????? ?? ?????? ???????? ??. ???? ???? — ??????? ?????????? ?????????? ??? ?????????????? ? ???????????. ?????? ? ????? ???????? ??????? ?????? ? ????!
innovationhub – Very helpful, platform simplifies advanced retail ideas for practical use.
Let me share with you something most septic companies refuse to: there are two types of people in this world. Those who assume septic systems are just “subterranean tanks for waste,” and those who have had raw sewage erupting into their yard at the dead of night. I learned this reality the hard way in 2005—waist-deep in sludge, trembling in a Washington deluge, as my brothers and I assisted a weathered installer fix our family’s collapsed system. I was a teenager. My hands blistered. My pants were destroyed. But that night, something clicked: This isn’t just dirt work. It’s folks’ lives that we’re protecting.
Let me share the ugly truth: most septic companies just maintain tanks. They are like quick-fix salesmen at a demolition convention. But Septic Solutions? They are unique. It all began back in the early 2000s when Art and his siblings—just kids barely tall enough to shoulder a shovel—assisted install their family’s septic system alongside a grizzled pro. Visualize this: three youngsters buried in Pennsylvania clay, discovering how soil absorption affects drainage while their friends played Xbox. “We didn’t just dig holes,” Art told me last winter, warm coffee cup in hand. “We discovered how earth whispers mysteries. A patch of cattails here? That’s Mother Nature yelling ‘high water table.'”
https://www.fitday.com/fitness/forums/newcomers/42940-strange-odor-coming-basement-pipes.html
Najlepsie online kasina https://betrating.sk/online-kasina/22bet/ na Slovensku – porovnajte licencie, bonusy, RTP, vyplaty a mobilne verzie. Pomozeme vam vybrat spolahlive kasino pre hru o skutocne peniaze a demo. Pravidelne aktualizujeme nase hodnotenia a propagacne akcie.
partnershipsstrategicclick – Appears structured and helpful for companies pursuing meaningful alliances.
??? ??????????? ?????? airstrait ??? ??????????? ?????? airstrait .
click for online growth – Easy-to-follow guides, digital concepts are presented clearly.
??????????? dyson airstrait pink dsn-vypryamitel-1.ru .
??? ?????? ??????????? ?????? dsn-vypryamitel.ru .
smoothbuyplatform – Fast and intuitive, online shopping feels seamless and simple.
shop without hassle – Appears clean and structured to reduce unnecessary steps.
Here’s the ugly truth: most HVAC failures take place because someone skipped a step. Failed to calculate the load properly. Used cheap equipment. Got wrong the insulation needs. We have fixed dozens of these disasters. And each time, we file away another learning. Like in 2017, when we decided on adding remote monitoring to each installation. Why? Because Sarah, our master tech, got sick of watching homeowners waste money on bad temperature settings. Now clients save hundreds yearly.
https://www.crunchbase.com/organization/product-air-heating-cooling-and-electric
?????? ??????????? ???? ??????????? vypryamitel-dn-kupit.ru .
alliances insight platform – Useful tips, simplifies how alliances operate in different markets.
AffordableBuyNetwork – Highlights cost-effective choices for digital shoppers.
??????????? ?????? https://team-black-top.ru ??? ????: ?????, ?????????, ?????????, ??????????????, ??????? ? ??????. ???????? ??????? ? Google/??????, ??????????? ?????? ? ??????. ?????????? ??????????, ???????? KPI ? ?????? ?? ????????? — ?? ?????? ?? ??????????? ?????.
learning mastery site – Encourages smarter habits and strategies for continuous growth.
Onlayn oyunlar üçün pinco casino azerbaijan maraql? imkanlar yarad?r. Sayt?n funksiyalar?n? yoxlamaq üçün link: pinco az?rbaycan. Telefon üçün pinco apk download m?nim üçün daha ?lveri?li oldu. Promosyonlar pinco casino giris zaman? görünür.
Pinko giris prosesi sad? v? sür?tlidir. Pinco az telegram üz?rind?n ?laq? saxlamaq mümkündür. Pinco oyna bölm?si il? oyunlara tez keçid var. Mobil idman m?rcl?ri üçün pinco az rahatd?r. ??xsi t?crüb?md? pinco stabil i?l?yir. Mobil istifad? üçün pinco casino uy?unla?d?r?l?b.
SmartStrategyTips – Offers insights that simplify even complex business planning.
??????????? ?????? ?????? ? ?????? ???????? vypryamitel-dn-kupit-2.ru .
learnfromexpertinsights – Excellent site, expert insights are practical and easy to apply today.
SEO-??????????? ????? https://seo-topteam.ru ? ?????? ? ???????? ?? 1 ???. ????????-??????, ???????????? ??????, ??????????? ??? ???????? ??????? ? ??????. ???????? ?? ???? ???????, ??????? ? ?????. ???????? ??? ??????? ? ?????.
dyson ??????????? ?????? ??? dyson ??????????? ?????? ??? .
??????????? ?????? ??????? ?????? ?????? dsn-vypryamitel-3.ru .
growth planning portal – Provides in-depth explanations for sustainable development and long-term results.
commercialbondhub – Provides clear and practical tips for secure commercial bonding transactions.
??? ??????????? ?????? ??? ?????? ??? ??????????? ?????? ??? ?????? .
?????? ???????????? ???? ? ?????????????? ???????? ? ?????? ???????????? ?????? Rosseriaall ?????????? ???????? ????????? ?????????? ???????? ??? ??????????? ??????-????????? ? ????? ??????? ?????. ??????? ???????? ??????? 2025 ???? ? ??????????? ???????? ???????, ????????????????? ?? ??????: ?????????, ?????????, ???????????? ???????, ??????? ?????, ??????? ? ???????? ???????. ?? ????? https://rosseriaall.net/ ?? ??????? ??? ?????????? ????????????? ??????? ????? “????? ?????????”, ??? ? ?????? ???????? ???????? ????. ??????? ????????? ????????? ?????? ????????? ??????? ?? ??????????, ? ?????????? ?????????? ??????????? ?????? ? ????? ?????????? ??????? ?????????????? ???????????.
marketwisdom – Insightful and actionable, the platform makes top strategies simple to follow.
ChoiceProTips – Practical and approachable advice, decision-making is simplified.
??????????? ??? ????? ?????? ?????? ??????????? ??? ????? ?????? ?????? .
PracticalSkillsOnline – Resource is user-friendly and delivers meaningful learning experiences.
direction first growth – Helpful resources, demonstrates how a clear path supports meaningful progress.
business trust resources – Hub provides clarity, forming meaningful relationships is easy.
innovative trade hub – Suggests staying ahead of market trends and adopting modern commerce practices.
?????? ??????? ?????? ??????? ?????? ??????? ?????? ??????? .
??????? ?????????????? https://ab-resurs.ru ??????? ??? ????????? ???????: ??????????, ????????, ??????????????, ?????????. ????? ??? ? ?????????, ?????? ? ???????, ????????????? ? ??????????? ????????, ???????? ? ????????? ?????????????.
bizsuccessinsights – Helpful content, actionable business tips are easy to digest and apply.
strategic market alliances – Easy to apply examples, shows how alliances work in real-world business situations.
?????? ??????????? ? ????? ?????? ??????????? ? ????? .
CorporatePartnerLink – Suggests a professional space for building enterprise-level alliances.
international shopping system – Platform seems designed to streamline worldwide e-commerce efficiently.
EasyShopOnline – User-friendly interface makes online shopping fast and enjoyable.
??????? ??????? ??? https://faamru.com ??? ????????? ??????? ?????? ????: ???????? ??????????, ????????, ????????????? ??????? ? ?????????. ???????????? ?????????????? ???????, ?????? ???? ??????, ???????? ? ???????????????? ??????.
flexible deal finder – Plenty of different options to look through comfortably.
collaborationhub – Guidance for cultivating alliances that are effective and transparent.
buyhub – Clear and practical, online transactions are streamlined for users.
online deals hub – Appears reliable, with fair prices and easy access to products.
?????? https://seoprofi.org/ ???????????????? ?? ?????????? ???????? ?????????? ??? Rutube ? VK ?????, ? ????? ?????????? ??????? ?? ???-????? ? ???????????? ?????????????? ???????????. ????????? ???????????? ????????? ????????? ?? ?????? 50-80%, ????????? ???????? ?? 1-3 ???? ? ?????????? ?????? ?? 1200 ?????? ?? 1000 ?????? ???????. ???????? ????????? ????????? ???????????? ????????, ????????? ?????? ?????? ?????????? ? ???????? ???????? ??????? ? ??? ??? ?????? ?????????? ??? ?????????????? ?????????.
BuildSmartFuture – Supports structured strategic planning without overwhelming new users.
BuySmartSecure – Reliable and user-friendly, finding products online is straightforward.
dyson ??????????? ?????? ? ?????? vypryamitel-dn.ru .
planforsuccess – Highlights planning, supports companies seeking organized growth pathways.
??????????? ????? dyson ht01 vypryamitel-dn-kupit-2.ru .
alliances knowledge click – Easy to browse, insights on global trust partnerships are clear.
??????????? ?????? ?????? ? ??????? vypryamitel-dn-2.ru .
https://wokerman.ru/
guides for clarity – Excellent explanations, makes learning concepts simpler.
dealtrustplatform – Emphasis on reliability, inspires confidence in online deals.
This is the brutal truth: the majority of HVAC failures happen because someone missed a step. Failed to calculate the load accurately. Used cheap equipment. Got wrong the insulation needs. We’ve fixed countless of these messes. And every time, we file away another insight. Like in 2017, when we decided on adding smart thermostats to all installation. Why? Because Sarah, our senior tech, got sick of watching homeowners burn money on inefficient temperature control. Now clients save 20-30% yearly.
https://fliphtml5.com/homepage/lweref/product-air-heating,-cooling,-and-electric/
enterprisetechframeworks – Well-organized content that makes enterprise framework concepts simple to understand.
UniversalShoppingHub – Reliable global store with smooth checkout and simple product discovery.
securecommercialalliances – Feels safe and reliable, guidance on alliances is clear and actionable.
valuehunter – Quickly locate good deals and enjoy a seamless shopping experience.
E-Commerce Insights Hub – Practical advice that simplifies online shopping decisions.
Work Skills Insight – Practical advice that boosted my professional confidence today.
marketrelationshipinsights – Informative and useful, guidance on managing market relationships is simple to follow.
??????????? ?????? ?????? ? ?????? ??????????? ?????? ?????? ? ?????? .
SmartShoppingHub – Easy-to-use interface, shopping online is straightforward and fast.
VenturePathway – Clear guidance and professional focus for exploring new ventures online.
??????? ?????? ?????? ????????? dn-pylesos.ru .
reliable shop portal – Layout is clear, making it simple to locate products and browse comfortably.
long-term success ideas – Insightful tips, content clearly outlines ways to achieve growth.
essential buys portal – Clean layout and fast load times provide a convenient shopping experience.
FuturePlannerHub – Easy-to-follow advice, strategic steps are explained thoroughly.
trusted partnership insights – Well-structured examples, makes alliance strategies easier to follow.
safebuyhub – Projects credibility, makes the experience of online shopping feel secure.
clarity engine – Very clear guidance, helps transform ideas into consistent momentum.
Allow me to tell you something nearly all septic companies will not: there are two types of people in this world. Those who assume septic systems are merely “underground boxes for waste,” and those who’ve had raw sewage erupting into their property at the dead of night. I learned this distinction the hard way in 2005—waist-deep in mud, trembling in a Washington deluge, as my brothers and I aided a grizzled installer repair our family’s failed system. I was a teenager. My hands ached. My pants were ruined. But that night, something changed: This is not just dirt work. It’s people’s lives that we’re safeguarding.
This is the harsh truth: most septic companies just maintain tanks. They are like quick-fix salesmen at a disaster convention. But Septic Solutions? They are special. It all originated back in the beginning of the 2000s when Art and his brothers—just kids hardly tall enough to shoulder a shovel—helped install their family’s septic system alongside a weathered pro. Imagine this: three youngsters knee-deep in Pennsylvania clay, learning how soil absorption affects drainage while their friends played Xbox. “We never just dig trenches,” Art shared with me last winter, hot coffee cup in hand. “We understood how ground whispers truths. A patch of wetland vegetation here? That’s Mother Nature screaming ‘high water table.'”
https://steemit.com/learn/@sarnalisa/drawing-study-for-septic-tank
SavvyShopperHub – Emphasizes smart spending and great value options.
ScaleWithKnowledge – Helpful guidance, growth strategy planning feels clear and manageable.
everydayoffershub – Practical and intuitive, spotting great deals online is quick.
Build Growth Insights – Offers fresh perspectives that help improve digital growth planning.
urbanretailcenter – User-friendly platform, browsing and shopping are fast and easy.
bizinsights – Concise and helpful, growth strategies are easy to understand and apply.
??????? ?????????????? https://ab-resurs.ru ??????? ??? ????????? ???????: ??????????, ????????, ??????????????, ?????????. ????? ??? ? ?????????, ?????? ? ???????, ????????????? ? ??????????? ????????, ???????? ? ????????? ?????????????.
Business Growth Guide – The explanations felt natural and helped me map things out with confidence.
Here’s the harsh truth: nearly all HVAC failures happen because someone skipped a step. Didn’t calculate the load accurately. Used undersized equipment. Miscalculated the insulation needs. We have fixed hundreds of these disasters. And each and every time, we file away another learning. Like in 2017, when we began adding WiFi controls to each install. Why? Because Sarah, our lead tech, got tired of watching homeowners burn money on inefficient temperature settings. Now clients save hundreds yearly.
https://www.blogger.com/profile/16467161244411992024
??????? ??????? ??? https://faamru.com ??? ????????? ??????? ?????? ????: ???????? ??????????, ????????, ????????????? ??????? ? ?????????. ???????????? ?????????????? ???????, ?????? ???? ??????, ???????? ? ???????????????? ??????.
BusinessKnowledgeClick – Practical and concise guidance for learning business effectively.
ProReliableAlliances – Focused on trust, enhancing the credibility of enterprise collaborations.
stepwise digital guide – Straightforward instructions, platform helps navigate digital planning smoothly.
market alliance strategies – Clear advice, helps connect theory to practical market scenarios.
alternative views space – Encourages exploring different ideas, sparking innovative thoughts.
proalliancebonds – Well-presented, emphasizes professional collaboration and business trust.
TopDiscountFinder – Smooth and reliable, shopping for bargains online is convenient.
shop securely now – Emphasizes safe transactions, making online buying stress-free.
PracticalGuidanceOnline – Clear tips that make solving problems simple and effective.
Discover Growth Lab – Informative content with actionable tips, makes strategy planning simple.
systematic growth – Very clear guidance, content supports deliberate and focused growth.
partnershippath – Informative and concise, framework strategies are explained in an easy-to-follow way.
trustedbusinessbonds – Very clear, platform presents commercial bond strategies in an understandable way.
frameworkfocus – Offers structured guidance for developing effective growth strategies.
AffordableShopLink – Designed for users who want the best deals online.
Connect for Business – A practical space where connecting with others feels intuitive.
LearnAndGrowHub – Very clear guidance, helped me grasp growth strategies quickly.
ForwardStrategyLab – Highlights methods for proactive planning without overcomplicating the process.
insightful learning click – Knowledge shared clearly, learning new ideas feels enjoyable and simple.
globalenterprisealliances – Informative platform, global alliance strategies are explained clearly and practically.
alliances guide hub – Very useful, real market examples enhance understanding of partnerships.
Angle Discovery Hub – Very intuitive layout, helps grasp market ideas efficiently.
secure business hub – Platform feels dependable, encouraging enterprises to connect confidently.
ClarityInBusiness – Helps make sense of strategies and operations in a simple way.
value buy portal – Clear navigation makes it easy to identify the best options.
successnavigator – Clear and practical, strategies are presented logically for easy use.
growthstrategyhub – Very clear explanations make digital growth planning approachable.
path to progress – Excellent tips, creates clarity on which actions lead to success.
SmartOnlinePurchases – Well-organized site, browsing and checkout are effortless.
???????? ?????? ?????? 2025 ????? ?????? ??????????? ????????
???????? ???? ?????? ??????? ?? ??????? ??????
learn more here – Clever setup, it encourages users to wander and explore naturally.
Future Commerce Ideas – The concepts feel modern and are explained in a way that’s simple to put into practice.
PersonalizedShopOnline – Encourages adaptable browsing and seamless selection for each shopper.
ModernShopHub – Very clear layout, makes understanding online shopping trends effortless.
Let me share the brutal truth: most HVAC failures take place because someone skipped a step. Failed to calculate the load accurately. Used undersized equipment. Misjudged the insulation needs. We have fixed countless of these disasters. And each time, we remember another learning. Like in 2017, when we began adding remote monitoring to all system. Why? Because Sarah, our master tech, got frustrated of watching homeowners waste money on inefficient temperature settings. Now clients save hundreds yearly.
https://linktr.ee/productairheating
Mobil telefondan pinco oyna seçimi m?nim üçün ?n böyük üstünlükdür. Buradan birba?a keçid etm?k mümkündür: pinco casino giris. Android istifad?çil?r üçün pinco casino apk download rahatd?r. Pinco casino azerbaycan bonus ??rtl?ri ayd?n göst?rilir.
Pinko giris prosesi sad? v? sür?tlidir. Pinco az?rbaycan tg kanal?nda yenilikl?r payla??l?r. Slot v? canl? oyunlar pinco gazino-da kifay?t q?d?rdir. Canl? oyunlar pinco az platformas?nda gecikm?sizdir. Pinko kazino il? ba?l? r?yl?r müxt?lifdir. Pinco casino az dil d?st?yi il? rahatd?r.
TrustedCorporateNetwork – Provides a secure and professional space for forming alliances.
trusted market partnerships – Insightful content, makes alliance concepts relatable and practical.
explore strategic choices – Easy-to-follow content, business strategies feel approachable.
GlobalOnlineBuyingHub – Found this resource valuable, explanations are concise and easy enough.
secureshopclick – Clear focus on safety, makes shopping feel risk-free and convenient.
NetworkingPro – Easy to engage with others, site provides trustworthy professional resources.
greenalliancespro – Useful and actionable, sustainability strategies for partnerships are clear.
onlinebuyhub – Intuitive and convenient, completing online purchases is fast and easy.
enterprise connections hub – Professional networking feels well-organized, with clear and trustworthy information.
growth mastery – Helpful strategies, makes planning and executing growth easier and more effective.
digital commerce hub – Modern feel enhances the browsing experience for shoppers.
GoalStrategyLab – Encourages methodical thinking to achieve strategic clarity and effectiveness.
MarketVisionPro – Informative and engaging, market ideas are simple to grasp and apply.
ClickTrustedEnterprise – Well-organized content, advice is actionable and reliable.
Business Collaboration Insights – Great guidance for building trust and long-term cooperation.
StrategicBusinessAlliances – Solid website with practical tips I can apply immediately today.
??????????? ??? ????? dyson airstrait ht01 ??????????? ??? ????? dyson airstrait ht01 .
?????? ???? ??? ??????????? ?????? vypryamitel-dsn-kupit.ru .
OMT’s standalone ?-learning alternatives empower independent exploration, supporting ? personal love for mathematics ?nd examination ambition.
Prepare f?r success in upcoming tests ?ith OMT Math Tuition’s exclusive curriculum,
?reated t? promote crucial thinking and self-confidence in ?very trainee.
Singapore’? focus on important believing through mathematics highlights the value of math tuition, ?hich assists students
develop th? analytical skills required ?y t?? nation’s forward-thinking syllabus.
Improving primary education ?ith math tuition prepares trainees f?r PSLE by cultivating ? growth f?ame ?f
mind t?ward challenging subjects ?ike proportion ?nd transformations.
Math tuition instructs effective t?me management techniques, assisting secondary pupils ful?
O Level exams within the alolocated period ?ithout
hurrying.
By offering extensive exercise ?ith pa?t A Level test papers, math tuition acquaints trainees
?ith inquiry styles ?nd marking plans f?r optimum performance.
OMT’? exclusive educational program improves MOE criteria ?ith a holistic technique that nurtures ?oth academic abilities
?nd ann enthusiasm f?r mathematics.
OMT’? s?stem i? easy to us? ?ne, ?o ?lso
beginners ?an browse and start boosting grades
?romptly.
By stressing theoretical understanding ??er rote knowing, math tuition gears up Singapore pupils for the advancing test layouts.
m? web site … sec 3 math tuition (https://websg1.s3.us-east-005.backblazeb2.com/math-tuition/4/key-metrics-for-assessing-tutor-effectiveness.html)
click for alliance insights – Well-structured advice, alliance concepts are easy to absorb.
??????????? dyson hs07 vypryamitel-dsn-kupit-1.ru .
?????? ??????????? dyson ????? vypryamitel-dsn-kupit-3.ru .
??????????? ?????? ?????? ? ????????????? ??????????? ?????? ?????? ? ????????????? .
??????????? dyson airstrait ht01 ???????? ??????????? dyson airstrait ht01 ???????? .
dyson ??????????? dyson ??????????? .
SavvyDealsHub – Focuses on affordability and convenience for online buyers.
???????? ???? https://priority-auto.ru/ – ?? ????????? ??????????? ?????????, ?????????, ???????? ?????????? ? ????????? ? ???????????? ???????, ? ???????? ?? ????????? ? ??????? ????????? ? ??. ??????? ??? ???? ????? ????????????? ?? ????? ??? ?????????????? ?????? “?????????? ?????????” – ??? ?? ??????? ???????? ????????? ????. ???????? ???? ??? ??? ??????, ?????? ?????????? ????????? ? ?????????, ??? ????? ??????????.
purchaseportal – User-friendly and efficient, shopping online is fast and stress-free.
FreshDealsOnline – Browsing and checkout are smooth, site feels user-friendly.
verifiedshoppinghub – Appears professional and safe, ideal for secure e-commerce experiences.
StrategicBondInsights – Clear and reliable, information about strategic bonds is well-presented and professional.
worldwideretailinsights – Practical platform, retail strategies from around the world are accessible and reliable.
??????????? dyson hs07 dsn-vypryamitel-1.ru .
?????? ???????????? ?????? ?????? ??????????? vypryamitel-dn-kupit.ru .
easy learning path – A comfortable space for ongoing education.
worldwide shopping portal – Diverse product range, easy to browse and purchase quickly.
PremiumOnlineBuyingHub – Well organized content that supports smarter decisions and planning efforts.
??? ??????????? ?????? airstrait vypryamitel-dn-kupit-1.ru .
StrategicPartnerLinks – Designed for professional alliances, prioritizing practical collaboration online.
dyson airstrait ?????? ??????????? dsn-vypryamitel.ru .
ClickForDecisionTools – Practical advice presented simply, makes evaluation easy.
ActionGuide – Easy-to-follow tips that lead to measurable improvements.
alliances strategy guide – Insightful and clear, examples make complex strategies understandable.
????? ?????????? ???????? ?? ???????????? ??? ????????? ????????? ? ???????? ???????? https://taximinivan54.ru/sheregesh.html ?? ???? ????? ? ??????? ??????? ?? ???????? ????? ???????? ??????????? ???????. ? ??????? ?????????? ??? ???? ???????? ? ??????????? ??????????. ????????, ??? ????????? ? ????? ??????? ????????! ???? ?????????????, ??? ??????. ????? ??????? ?? 7 ?????. ?????????? ?? ???????, ???? ?????? ???? ??????. ?????????? ??? ????, ???? ?????????, ?????? ???? ????????.
International Retail Hub – Very useful for tracking retail developments across different markets.
???????????????? ????????? ?????????? ????? ?????????, ????? ???????????? ????????????? ????????? ?????????? ?????????? ????????? ??????????? ??????????? ???????????? ? ???????? ????????. ???????? Aprazer ???????????????? ?? ????????? ??????????? ????????????, ??????? ????????? ??? ??????? ????????? ???????? ? ? ?????????????? ???????????. ?????? ??????? ???????? ???????????????? ???????????, ??? ??????????? ??? ??????????? ? ?????????????. ?? ????????? https://aprazer.com.ru/ ??????????? ?????? ??????? ? ?????????? ??????????, ??????? ?????????? ???????? ??????????? ????? ??????????? ???? ?????? ? ??????????? ???????? ???????????? ??????????????? ????????????. ???????? ???????? ???????? ? ???????????????, ??????????? ?????????? ???????? ? ?????? ????????? ?? ????????????? ????????? ?? ???????????????? ?????.
secure business strategies – Offers actionable guidance, connecting with partners feels natural.
useful link – Smooth interface, concise sections, very readable content
?????? ??????????? ?????? ??????? dsn-vypryamitel-3.ru .
ProAllianceAdvisor – Insightful and structured, professional partnerships are easier to manage.
I need to explain something most septic companies refuse to: there are two types of people in this world. Those who believe septic systems are just “subterranean tanks for waste,” and those who have had raw sewage bubbling into their backyard at 2 AM. I discovered this difference the tough way in 2005—waist-deep in mud, trembling in a Washington downpour, as my siblings and I helped a grizzled installer restore our family’s collapsed system. I was a teenager. My hands were raw. My jeans were ruined. But that moment, something crystallized: This ain’t just dirt work. It’s people’s lives that we’re protecting.
This is the ugly truth: the majority of septic companies just service tanks. They act like band-aid salesmen at a chainsaw convention. But Septic Solutions? They’re unique. It all originated back in the early 2000s when Art and his brothers—just kids hardly tall enough to lift a shovel—aided install their family’s septic system alongside a experienced pro. Visualize this: three youngsters waist-deep in Pennsylvania clay, discovering how soil absorption affects drainage while their friends played Xbox. “We didn’t just dig trenches,” Art explained to me last winter, steaming coffee cup in hand. “We discovered how soil whispers mysteries. A patch of wetland vegetation here? That’s Mother Nature screaming ‘high water table.'”
https://www.fitday.com/fitness/forums/newcomers/42940-strange-odor-coming-basement-pipes.html
networkhub – Extremely useful, offers clear ways to build professional connections.
PathToDigitalGrowth – Provides actionable guidance that feels organized and trustworthy.
??? ??????????? ?????? ?????? ? ?? ??????????????? vypryamitel-dsn-kupit.ru .
business connectivity hub – Highlights global networking opportunities and cross-border relationships.
??? ??????????? ?????? ???????? vypryamitel-dsn-kupit-3.ru .
??????????? ?????? hs07 ?????? vypryamitel-dsn-kupit-2.ru .
?????? ??????????? ????? ?????? ? ?????? vypryamitel-dn-kupit-3.ru .